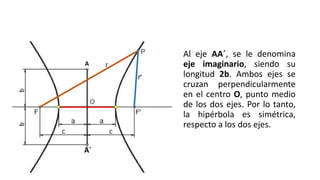
La hipérbola es una curva plana con dos ramas definida como el lugar geométrico de puntos cuya diferencia de distancias a dos puntos fijos llamados focos es constante. Tiene dos ejes perpendiculares, el eje real y el eje imaginario, que se cruzan en el centro. Las ecuaciones de una hipérbola con centro en el origen relacionan las coordenadas x e y con los semiejes real e imaginario y la distancia focal.

1. HIPÉRBOLA
UNIVERSIDAD AUTÓNOMA DE YUCATÁN
ESCUELA PREPARATORIA DOS
MODELACIÓN MATEMATICA
• Guerrero Cruz Diego 2°11

2. DEFINICIÓN
La hipérbola es una curva
abierta y plana, con dos
ramas, que se define como el
lugar geométrico de los
puntos del plano cuya
diferencia de distancias r’–r,
a dos puntos fijos F y F’,
denominados focos, es
constante e igual a 2a,
siendo 2a la longitud del eje
real de la hipérbola.
A
A´

3. Al eje AA´, se le denomina
eje imaginario, siendo su
longitud 2b. Ambos ejes se
cruzan perpendicularmente
en el centro O, punto medio
de los dos ejes. Por lo tanto,
la hipérbola es simétrica,
respecto a los dos ejes.
A
A´

5. Escriba aquí la ecuación.
EJE REAL
ASÍNTOTAS
HIPÉRBOLA

6. Escriba aquí la ecuación.
EJE
IMAGINARIO
ASÍNTOTAS
HIPÉRBOLA

7. Escriba aquí la ecuación.
b
c a
𝒂 𝟐
+ 𝒃 𝟐
= 𝒄 𝟐
ASÍNTOTAS
HIPÉRBOLA

8. Ecuaciones de una hipérbola con centro el origen
HIPÉRBOLA HORIZONTAL HIPÉRBOLA VERTICAL
𝑥2
𝑎2
−
𝑦2
𝑏2
= 1
𝑦2
𝑎2
−
𝑥2
𝑏2
= 1
Focos (−𝑐, 0) (𝑐, 0)
Vértices (−𝑎, 0) y (𝑎, 0)
Focos (0, −𝑐) (0, 𝑐)
Vértices (0, −𝑎) y (0, 𝑎)
Extremos del eje imaginario
(0, −𝑏) y (0, 𝑏)
Extremos del eje imaginario
(−𝑏, 0) y (𝑏, 0)
En ambas hipérbolas la longitud del Lado recto =
2𝑏2
𝑎
La excentricidad es =
𝑐
𝑎

9. HipérbolaSemieje real 𝑎 = 4
Semieje imaginario 𝑏 = 3
𝒙 𝟐
𝟏𝟔
−
𝒚 𝟐
𝟗
= 𝟏
𝑐2
= 𝑎2
+ 𝑏2
𝑐2 = 16 + 9 = 25
𝑐 = 5
Focos (-5,0) (5,0)
Eje Real=8
Eje imaginario = 6
Distancia focal = 10
Lado recto = 4.5
Excentricidad = 1.25

10. Semieje real 𝑎 = 4
Semieje imaginario 𝑏 = 4
𝒚 𝟐
𝟏𝟔
−
𝒙 𝟐
𝟏𝟔
= 𝟏 ⇒ 𝒚 𝟐 − 𝒙 𝟐 = 𝟏𝟔
𝑐2 = 𝑎2 + 𝑏2
𝑐2 = 16 + 16 = 32
𝑐 = 32
Focos (0,- 32) (0, 32)
Eje Real=8
Eje imaginario = 8
Distancia focal = 2 32
Lado recto = 8
Excentricidad = 32/4