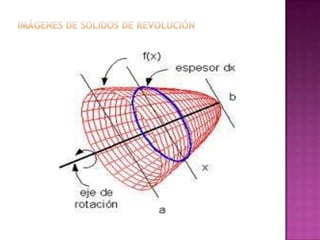
Este documento describe cómo calcular el volumen de un sólido de revolución usando el método de discos. Explica que si se rota una función alrededor de un eje, la integral de 2πrf(x)dx entre los límites calcula el volumen generado, donde r es el radio y f(x) la altura. También cubre cómo calcular volúmenes con cavidades y rotaciones alrededor de otros ejes.

2.  Se denomina sólido de
revolución o volumen de
revolución, al sólido obtenido
al rotar una región del plano
alrededor de una recta
ubicada en el mismo, las
cuales pueden o no
intersecarse. Dicha recta se
denomina eje de revolución.
 Sea f una función continua y
positiva en el intervalo [a,b].
Si la región R indicada en la
figura rota alrededor del eje
X, está genera un sólido de
revolución cuyo volumen
tratamos de determinar.

3.  Usaremos para el cálculo del volumen de
revolución el llamado método de discos.
 Observando que las secciones transversales que se
generan son discos de radio r = f(x) con y
recordando que el volumen de un cilindro es
 Si rotamos la función y = f(x) alrededor del eje x ,
con x entre a y b, la integral siguiente

 calcula el volumen del sólido generado.
 Con la sentencia anterior podemos calcular el
volumen poniendo en la opción output = integral y
con la opción output = value calculamos el valor
numérico de la integral.

4.  Volumen de un sólido de revolución con
cavidades
 En los siguientes ejemplos desarrollados veremos dos
dificultades en el cálculo del volumen, una es la
rotación de un área a través de otro eje que no es el
eje coordenado, y la otra dificultad es el cálculo de
volúmenes de sólidos con cavidad, cuyas secciones
transversales son coronas o arandelas.
 Tendrá más éxito en hallar el volumen si le dedica
tiempo necesario al dibujo de las figuras.
 No improvise!! Sólo es necesario tener en cuenta
cómo hallar el área de una sección transversal del
sólido.
 Observación: La variable de integración depende del
eje alrededor del cual gira la región; la rotación
alrededor del eje x requiere integración respecto de
la variable x ; mientras que la rotación alrededor del
eje y requiere integración respecto de la variable y.
 Primer ejemplo:
 Sea la región limitada por y=x e