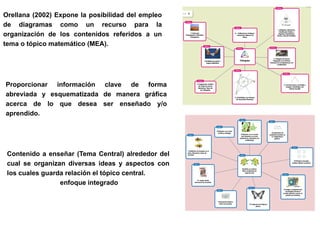
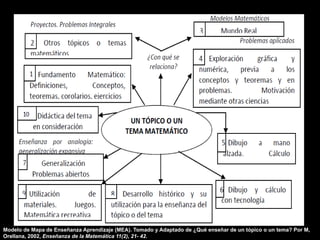
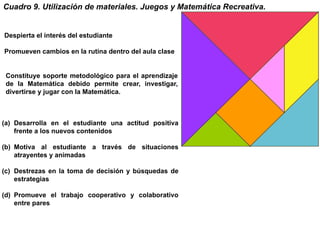
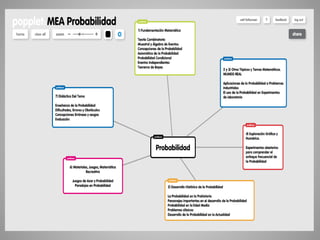
Este documento presenta el Mapa de Enseñanza-Aprendizaje como un modelo para organizar el contenido matemático. El mapa incluye 10 cuadros que cubren aspectos como los fundamentos matemáticos, la exploración gráfica y numérica, el desarrollo histórico y la didáctica del tema. El objetivo es proveer una visión más integral de la matemática que vaya más allá de la mera presentación de conceptos.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
UNIVERSIDAD PEDAGÓGICA EXPERIMENTAL LIBERTADOR
INSTITUTO PEDAGÓGICO DE MARACAY “RAFAEL ALBERTO ESCOBAR LARA”
DEPARTAMENTO DE MATEMÁTICA
Línea de Investigación en Tecnologías de la Información y Comunicación
en Educación Matemática (LITICEM)
EL MAPA DE ENSEÑANZA-APRENDIZAJE COMO MODELO
ORGANIZADOR DEL CONTENIDO MATEMÁTICO
Facilitador: Prof. Yerikson Suárez Huz
Septiembre 2017

2. INTRODUCCIÓN
La matemática ha sido una constante en la
evolución y desarrollo de las civilizaciones
Las ideas matemáticas han sido resultado de
un prolongado proceso intelectual y social,
cuyas raíces se esconden en el remoto pasado
Ayuda a comprender el universo
Ofrece soluciones a diversidad de problemas
Capacidad de respuestas y desarrollo a la
sociedad
Aplicaciones a gran cantidad de áreas del
conocimiento
Disciplina viva, Forma parte del acervo cultural
Planteamiento

3. Sin embargo
La visibilidad de la Matemática y su
importancia sigue siendo limitada
Impopularidad y desconocimiento de la
disciplina
En su enseñanza aún abunda al enfoque
basado en la exposición por parte del docente
de los contenidos.
Visión depositaria del estudiante.
Percepción según la cual :
 La matemática es para unos pocos
 No tiene ninguna utilidad en la realidad.
 Aprendizaje mecánico, repetitivo,
memorístico, netamente procedimental

4. Parece necesario
 Abordar los procesos de aprendizaje que
involucra el estudio de la Matemática
 Analizar los métodos de enseñanza
 Reconocer la naturaleza de los objetos
matemáticos (origen, aplicación,
comprensión, visiones)
 Estudiar elementos claves en la formación
inicial de aquellos quienes enseñan
matemática
 Estudiar los posibles recursos, materiales y
herramientas que contribuyan al proceso de
E-A de la Matemática.
Un elemento clave presente:
El dominio del contenido matemático por parte de quien enseña y aprende.
¿Qué enseñar sobre un contenido matemático?, y ¿cómo enseñarlo? son
preguntas claves que constantemente debe hacerse quien enseña
matemática

5. Las actividades que lleva a cabo el profesor
están supeditadas al currículum escolar, la
institución, la audiencia, y las políticas educativas
La Planificación en la Enseñanza de la Matemática
Proceso anticipado al acto educativo dentro y
fuera del aula. Pretende crear las mejores
condiciones para el logro del aprendizaje.
El docente debe ser capaz de ordenar, disponer y
organizar los contenidos dentro de su ámbito de
acción.
Prever qué contenidos enseñar, por qué, cómo
hacerlo, cómo integrarlos, qué actividades poner
en práctica y cómo evaluar el desempeño de los
estudiantes y la efectividad del proceso.

6. Mapa de Enseñanza-Aprendizaje (MEA)
Mauricio Orellana Chacín

7. Orellana (2002) Expone la posibilidad del empleo
de diagramas como un recurso para la
organización de los contenidos referidos a un
tema o tópico matemático (MEA).
Contenido a enseñar (Tema Central) alrededor del
cual se organizan diversas ideas y aspectos con
los cuales guarda relación el tópico central.
enfoque integrado
Proporcionar información clave de forma
abreviada y esquematizada de manera gráfica
acerca de lo que desea ser enseñado y/o
aprendido.

8. El diseño y elaboración del MEA puede variar de
un docente a otro.
La numeración dada no debe ser entendida
como trabajo secuencial y progresivo
Es posible suprimir y/o agregar cuadros si así lo
considera pertinente el docente
La organización no es jerárquica
El tiempo disponible para la enseñanza la
programación del año escolar
Conocimiento del tema: Es importante el
dominio del contenido matemático de parte del
profesor
Intereses de los estudiantes y de los docentes,
Nivel educativo
Consideraciones a la hora de
diseñar el MEA

9. Modelo de Mapa de Enseñanza Aprendizaje (MEA). Tomado y Adaptado de ¿Qué enseñar de un tópico o un tema? Por M,
Orellana, 2002, Enseñanza de la Matemática 11(2), 21- 42.

10. Cuadro 1. Fundamento Matemático
Conceptos, propiedades, axiomas, teoremas,
relaciones, enfoques, simbología y lenguaje
Este cuadro es donde hacen énfasis los
docentes a la hora de dar sus clases de
Matemática.
Pero esta visión de la enseñanza desde una
visión lineal, inamovible y de presentación y
exposición de una Matemática acabada, formal
y rigurosa parece no ser suficiente

11. Cuadros 2 y 3. Otros tópicos o temas de Matemática y el Mundo real
Inclusión de Modelos Matemáticos
Visión más realista de la Matemática
Conexión con el mundo real
Problemas Integradores

12. Cuadro 4. Exploración Gráfica y Numérica previa.
Estudio previo de algunos problemas y/o
situaciones claves antes de presentar contenido
Experimentación (gráfica, numérica, o ambas) que
pretende
detección de patrones
identificación de conjeturas
formulación de hipótesis.
Los contextos de exploración favorecen la
comprensión de la Matemática

13. Cuadro 5 y 6. Dibujo a mano alzada y cálculo manual; dibujo y cálculo con
tecnología
La destreza en el dibujo y en el cálculo manual
son dos capacidades importantes de quien
aprende Matemática.
Su práctica se ha visto complementada con el
uso de los software de geometría dinámica
(SGD), y los software de cálculo simbólico (SCS)
Posibilitan explorar, descubrir, reformular,
conjeturar, validar o refutar, sistematizar
Capacidad para facilitar diversos modos de
representación y de manipulación de los objetos
matemáticos

14. Cuadro 7. Generalización y problemas abiertos
La generalización es clave en la Matemática
procesos cognitivos complejos que deben ser exhibidos
por los estudiantes de forma progresiva, desde una
posición activa del estudiante y no una contemplativa.
Generalización de patrones matemáticos

15. Cuadro 8. Desarrollo histórico y su utilización para la enseñanza del tópico
Anécdotas --- biografías --- Estudios
Históricos-Epistemológicos
Matemática como actividad humana
búsqueda de respuestas y soluciones a
problemas enmarcados temporal,
cultural, social y geográficamente.
Pretende
(a) Promover un cambio de actitud hacia la Matemática,
(b) Exponer obstáculos epistemológicos
(c) Servir como elemento integrador de la Matemática con otras disciplinas
(d) Fomentar el interés y la motivación de las personas hacia la Matemática.

16. Cuadro 9. Utilización de materiales. Juegos y Matemática Recreativa.
Despierta el interés del estudiante
Promueven cambios en la rutina dentro del aula clase
Constituye soporte metodológico para el aprendizaje
de la Matemática debido permite crear, investigar,
divertirse y jugar con la Matemática.
(a) Desarrolla en el estudiante una actitud positiva
frente a los nuevos contenidos
(b) Motiva al estudiante a través de situaciones
atrayentes y animadas
(c) Destrezas en la toma de decisión y búsquedas de
estrategias
(d) Promueve el trabajo cooperativo y colaborativo
entre pares

17. Cuadro 10. Didáctica del tema en consideración.
Organizar el modo en que llevaría a cabo el proceso de
enseñanza
Cómo se aprenden esos objetos matemáticos
Conocimientos previos, concepciones y creencias

19. Gracias por
su atención
El placer por el descubrimiento y la comprensión de la Matemática es
un camino que se puede recorrer acompañado de la tecnología.