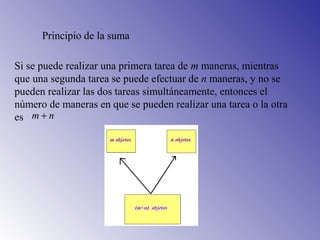
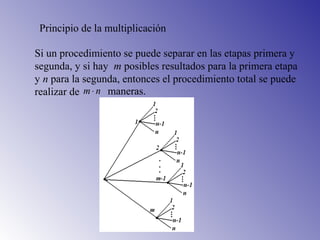
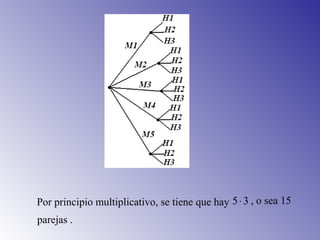
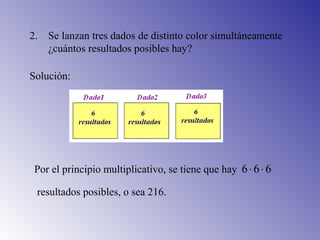
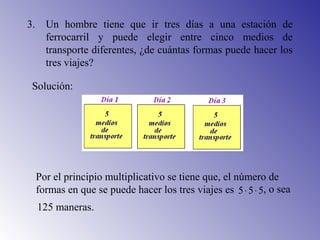
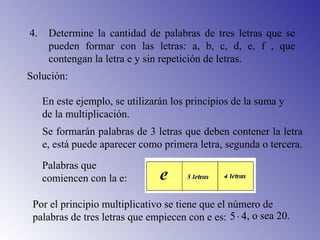
El documento presenta los principios fundamentales de conteo, incluyendo el principio de la suma y el principio de la multiplicación. Estos principios se utilizan para resolver problemas de conteo como el número de maneras de elegir libros de una biblioteca, resultados posibles de lanzar dados, y ensaladas que se pueden preparar con diferentes verduras. El documento también incluye ejemplos y ejercicios para aplicar estos principios.

1. DE
Enero 2009
Luis Acosta Romero
Sergio Yansen Núñez
TÉCNICAS
CONTEO

2. Principios fundamentales de conteo
En esta clase se mostrarán y ejemplificarán los principios
básicos que rigen las técnicas de conteo, las cuales son los
puntos de partida de técnicas más específicas como la
combinatoria y la permutación.
Estos principios tienen importancia no sólo a nivel teórico,
como fundamento de nuevos conceptos, sino también a
nivel operacional, pues su utilización práctica ayuda a
complementar otras técnicas.

3. Principio de la suma
Si se puede realizar una primera tarea de m maneras, mientras
que una segunda tarea se puede efectuar de n maneras, y no se
pueden realizar las dos tareas simultáneamente, entonces el
número de maneras en que se pueden realizar una tarea o la otra
es nm +

4. Ejemplos a desarrollar en clases por el profesor:
1. La biblioteca de una Universidad tiene 43 libros de
Administración y 82 libros de Matemática ¿De cuántas
maneras un estudiante puede elegir un texto en alguno de
los temas?
Solución:
Usando el principio de la suma: 43+82=125
Por lo tanto, un estudiante puede elegir un texto en
alguno de los temas de 125 maneras.

5. 2. Se lanzan dos dados simultáneamente (los dados no se
pueden distinguir entre sí) ¿cuántos resultados hay?
Solución:
Esquematizando las posibilidades:
11 12 13 14 15 16
21 22 23 24 25 26
31 32 33 34 35 36
41 42 43 44 45 46
51 52 53 54 55 56
61 62 63 64 65 66
Note que ij significa que en un dado se obtuvo i y en el otro j.

6. Contaremos aquellas duplas de números iguales:
11 , 22 , 33 , 44 , 55 , 66. 6 posibilidades
Quedan 36-6=30 posibilidades:
12 13 14 15 16
21 23 24 25 26
31 32 34 35 36
41 42 43 45 46
51 52 53 54 56
61 62 63 64 65

7. De estas 30 posibilidades, se tiene que los 15 pares superiores
a la diagonal, son equivalentes a los pares inferiores a la
diagonal. Por tanto, contaremos 15 posibilidades más.
Luego, por el principio de la suma se tiene que hay 6+15
resultados, o sea 21.

8. 3. ¿Cuántas ensaladas pueden prepararse con lechuga, repollo y
apio?
Solución:
Contaremos:
Ensaladas que se pueden formar con sólo una verdura: 3
posibilidades (lechuga – repollo – apio)
Ensaladas que se pueden formar con sólo dos verduras: 3
posibilidades (lechuga-repollo , lechuga-apio , repollo-apio)
Ensaladas que se pueden formar con las tres verduras: 1
posibilidad
Luego, por el principio de la suma se tiene que se pueden
preparar 3+3+1 ensaladas, o sea 7.

9. Principio de la multiplicación
Si un procedimiento se puede separar en las etapas primera y
segunda, y si hay m posibles resultados para la primera etapa
y n para la segunda, entonces el procedimiento total se puede
realizar de nm⋅ maneras.

10. Ejemplos a desarrollar en clases por el profesor:
1. El director de teatro de una escuela debe seleccionar a una
dama y a un varón para la obra final de temporada, y
escogerá de un grupo constituido por 5 mujeres y 3
hombres que han cumplido todas las exigencias ¿De
cuántas maneras podrá escoger una mujer y un hombre
para que interpreten los roles protagónicos?
Solución:
Sean M1 , M2 , M3 , M4, M5 las mujeres y H1, H2 , H3 los
hombres
En el gráfico siguiente se muestran las posibilidades:

11. Por principio multiplicativo, se tiene que hay 35⋅ , o sea 15
parejas .

12. 2. Se lanzan tres dados de distinto color simultáneamente
¿cuántos resultados posibles hay?
Solución:
Por el principio multiplicativo, se tiene que hay 666 ⋅⋅
resultados posibles, o sea 216.

13. 3. Un hombre tiene que ir tres días a una estación de
ferrocarril y puede elegir entre cinco medios de
transporte diferentes, ¿de cuántas formas puede hacer los
tres viajes?
Solución:
Por el principio multiplicativo se tiene que, el número de
formas en que se puede hacer los tres viajes es 555 ⋅⋅ , o sea
125 maneras.

14. 4. Determine la cantidad de palabras de tres letras que se
pueden formar con las letras: a, b, c, d, e, f , que
contengan la letra e y sin repetición de letras.
En este ejemplo, se utilizarán los principios de la suma y
de la multiplicación.
Solución:
Se formarán palabras de 3 letras que deben contener la letra
e, está puede aparecer como primera letra, segunda o tercera.
Palabras que
comiencen con la e:
Por el principio multiplicativo se tiene que el número de
palabras de tres letras que empiecen con e es: 45⋅ , o sea 20.

15. Palabras que tengan
la e en el medio
Por el principio multiplicativo se tiene que el número de palabras
de tres letras que tienen la e en medio es: 45⋅ , o sea 20.
Palabras que terminen con e:
Por el principio multiplicativo se tiene que el número de palabras
de tres letras que terminan con e es: 45⋅ , o sea 20.
Por el principio de la suma se tiene que la cantidad de
palabras de tres letras que se pueden formar que contengan la
letra e y sin repetición de las letras a, b, c, d, f es:
202020 ++ o sea 60 palabras.

16. Guía de ejercicios
1. ¿De cuántas formas pueden sentarse seis hombres y siete
mujeres en una fila de modo que las mujeres ocupen los
sitios impares?
2. Dadas las letras: A , B , C , D , E , F , G , L ,
a) ¿Cuántas palabras de 9 letras se pueden formar?
b) ¿Cuántas palabras de 9 letras se pueden formar, si las
vocales deben quedar juntas?
3. Dadas la letras de la palabra CONSTRUCCION
a) ¿Cuántas palabras de 12 letras se pueden formar?
b) ¿Cuántas palabras de 12 letras se pueden formar, si las
vocales deben quedar juntas?

17. 4. Dadas las letras de la palabra CONSTITUCION
¿Cuántas palabras diferentes de 12 letras se pueden
formar, si las consonantes deben quedar juntas?
5. Dadas las letras A , A , A , B , C , D , N , N , P , P
a) ¿Cuántas palabras diferentes de 10 letras se pueden
formar?
b) ¿Cuántas palabras diferentes de 10 letras se pueden
formar, si las letras iguales deben quedar juntas?
6. ¿De cuántas maneras se puede elegir una comisión de seis
personas de entre diez personas?
7. ¿De cuántas maneras puede escogerse un comité, compuesto
de tres hombres y dos mujeres, de un grupo de siete hombres
y cinco mujeres?

18. 8. Un alumno debe responder un Examen de 10 preguntas. Él
aprueba el Examen si responde, correctamente, al menos
6 preguntas. ¿De cuántas maneras puede el estudiante
responder el Examen, para aprobarlo?
9. De un total de cinco matemáticos y siete físicos, se forma un
comité de dos matemáticos y tres físicos, ¿de cuántas formas
puede formarse, si
a) puede pertenecer a él cualquier matemático o físico?
b) un físico determinado debe pertenecer al comité?
c) dos matemáticos determinados no pueden estar en el
comité?
10. Dadas consonantes (distintas) y vocales (distintas).
¿Cuántas palabras pueden formarse con dos vocales y seis
consonantes?