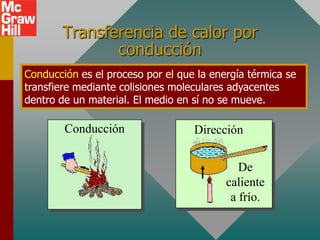
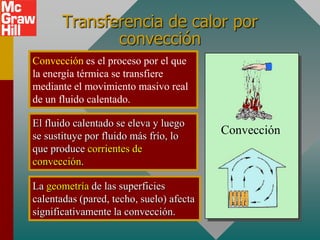
Este documento presenta los conceptos clave de la transferencia de calor a través de la conducción, convección y radiación. Explica la conductividad térmica y cómo se transfiere el calor a través de los materiales. También cubre la tasa de radiación y cómo se calcula la potencia radiada desde una superficie caliente. Proporciona ejemplos numéricos para ilustrar los principios.

1. Transferencia de calor
Presentación PowerPoint de
Paul E. Tippens, Profesor de Física
Southern Polytechnic State University

2. LA TRANSFERNCIA DE CALOR se
minimiza mediante múltiples capas de
revestimiento beta. Este y otros materiales
aisladores protegen la nave espacial de
condiciones ambientales hostiles. (NASA)

3. Objetivos: Después de terminar
esta unidad, deberá:
• Demostrar su comprensión de
conducción, convección y radiación, y
dar ejemplos.
• Resolver problemas de conductividad
térmica con base en cantidad de calor,
longitud de trayectoria, temperatura,
área y tiempo.
• Resolver problemas que involucran la
tasa de radiación y la emisividad de
superficies.

4. Transferencia de calor por
conducción
Conducción es el proceso por el que la energía térmica se
transfiere mediante colisiones moleculares adyacentes
dentro de un material. El medio en sí no se mueve.
Conducción Dirección
De
caliente
a frío.

5. Transferencia de calor por
convección
Convección es el proceso por el que
la energía térmica se transfiere
mediante el movimiento masivo real
de un fluido calentado.
El fluido calentado se eleva y luego
se sustituye por fluido más frío, lo
Convección
que produce corrientes de
convección.
La geometría de las superficies
calentadas (pared, techo, suelo) afecta
significativamente la convección.

6. Transferencia de calor por radiación
Radiación es el proceso por el que
la energía térmica se transfiere
mediante ondas electromagnéticas.
Radiación
Atómico
Sol
¡No se requiere medio!

7. Tipos de transferencia de calor
Considere la operación de una cafetera común:
Piense en cómo se
transfiere calor por:
¿Conducción?
¿Convección?
¿Radiación?

8. Corriente calorífica
La corriente calorífica H se define como la
cantidad de calor Q transferida por unidad de
tiempo  en la dirección de mayor temperatura
a menor temperatura.
vapor hielo
Q
H ( J / s)

Unidades típicas son: J/s, cal/s y Btu/h

9. Conductividad térmica
La conductividad térmica k de un
material es una medida de su t1 t2
habilidad para conducir calor.
H = corriente calorífica (J/s)
A = área superficial (m2)
Dt = diferencia de temperatura Dt = t2 - t1
L = grosor del material
kADt
Q QL
H  k Unidades 
J
 L A Dt s  m  C

10. Las unidades SI para conductividad
Caliente Frío QL
k
A Dt
Para cobre: k = 385 J/s m C0
En unidades SI,this means that mediciones
Taken literally, por lo general for a 1-m length
pequeñas whose cross y área is 1 deben
of copper de longitud L section A se m2 and
convertir a points y metros cuadrados,
whose endmetros differ in temperature by 1 C0,
respectivamente, antes at the rate of 1fórmulas.
heat will be conducted de sustituir en J/s.

11. Unidades antiguas de conductividad
Dt = 1 F0 Unidades antiguas, todavía
1h activas, usan mediciones
A=1 ft2 comunes para área en ft2, tiempo
en horas, longitud en pulgadas y
Q=1 Btu
cantidad de calor en Btu.
L = 1 in. k de vidrio = 5.6 Btu in/ft2h F0
Tomado literalmente, esto significa que, para una
placa de vidrio de 1 in de espesor, cuya área es 1
ft2 y cuyos lados difieren en temperatura por 1 F0,
el calor se conducirá a la tasa de 5.6 Btu/h.

12. Conductividades térmicas
A continuación se dan ejemplos de los dos sistemas de
unidades para conductividades térmicas de materiales:
Material J/s  m  C o
Btu  in/ft 2  h  F0
Cobre: 385 2660
Concreto o 0.800 5.6
vidrio:
Tablero de 0.040 0.30
corcho:

13. Ejemplos de conductividad térmica
Comparación de corrientes caloríficas para condiciones
similares: L = 1 cm (0.39 in); A = 1 m2 (10.8 ft2); Dt = 100 C0
Aluminio: 2050 kJ/s 4980 Btu/h
3850 kJ/s 9360 Btu/h
Cobre:
Concreto o 8.00 kJ/s 19.4 Btu/h
vidrio:
Tablero de 0.400 kJ/s 9.72 Btu/h
corcho:

14. Ejemplo 1: Una gran ventana de vidrio mide 2 m
de ancho y 6 m de alto. La superficie interior está
a 20 0C y la superficie exterior a 12 0C. ¿Cuántos
joules de calor pasan a través de esta ventana en
una hora? Suponga L = 1.5 cm y que k = 0.8 J/s
m C0.
A = (2 m)(6 m) = 12 m 2 200C 120C
kADt kADt
A =1h
Q
H  ; Q
 L L Q = ¿?
(0.8 J/m  s  C0 )(12 m 2 )(8 C0 )(3600 s)
Q Dt = t2 - t1
0.0150 m
= 8 C0
0.015 m
Q = 18.4 MJ

15. Ejemplo 2: La pared de una planta congeladora
está compuesta de 8 cm de tablero de corcho y 12
cm de concreto sólido. La superficie interior está a
-200C y la superficie exterior a +250C. ¿Cuál es la
temperatura de la interfaz ti?
Nota:  H 
 
H
  -200C
ti
250C
 A corcho  A concreto
k1 ti  (200 C) 
  k2  250 C - ti 
  H
 A
L1 L2
k1 (ti  20 C) k2 (25 C - ti )
0 0 Flujo
 estacionario
L1 L2 8 cm 12 cm

16. Ejemplo 2 (Cont.): Encontrar la temperatura
de interfaz para una pared compuesta.
ti
k1 (ti  20 C) k2 (25 C - ti )
0 0
-200C 250C

L1 L2
H
Al reordenar factores se obtiene:
A
k1L 2
(ti  200 C)  (250 C - ti ) Flujo
estacionario
k2 L1
8 cm 12 cm
k1L2 (0.04 W/m  C0 )(0.12 m)
  0.075
k2 L1 (0.8 W/m  C )(0.08 m)
0

17. Ejemplo 2 (Cont.): Al simplificar se obtiene:
ti
(0.075)(ti  20 C)  (25 C - ti )
0 0
-200C 250C
0.075ti + 1.50C = 250C - ti
H
De donde: ti = 21.90C A
Conocer la temperatura de interfaz Flujo
estacionario
ti permite determinar la tasa de flujo
de calor por unidad de área, H/A. 8 cm 12 cm
La cantidad H/A es igual para corcho o concreto:
kADt H k Dt
Q
H  ; 
 L A L

18. Ejemplo 2 (Cont.): Flujo estacionario constant
H/A es constante en el tiempo, de modo ti
que diferentes k producen diferentes Dt -200C 250C
Corcho: Dt = 21.90C - (-200C) = 41.9 C0
H
Concreto: Dt = 250C - 21.90C = 3.1 C0 A
kADt H k Dt
Q Flujo
H  ;  estacionario
 L A L 8 cm 12 cm
Dado que H/A es el mismo, elija sólo concreto:
H k Dt (0.8 W/mC0 )(3.1 C0 ) H
   20.7 W/m 2
A L 0.12 m A

19. Ejemplo 2 (Cont.): Flujo estacionario constant
H ti
 20.7 W/m 2 -200C 250C
A
H
Corcho: Dt = 21.90C - (-200C) = 41.9 C0
A
Concreto: Dt = 250C - 21.90C = 3.1 C0
Flujo
estacionario
Note que 20.7 Joules de calor por
8 cm 12 cm
segundo pasan a través de la pared
compuesta. Sin embargo, el
intervalo de temperatura entre las Si A = 10 m2, el
caras del corcho es 13.5 veces más flujo de calor en 1
grande que para las caras del h sería ______
745 kW
concreto.

20. Radiación
La tasa de radiación R es la energía emitida por
unidad de área por unidad de tiempo (potencia
por unidad de área).
Tasa de radiación Q P P
R  R   es T 4
(W/m2): A A A
Emisividad, e : 0>e >1
Constante de Stefan-Boltzman:
s = 5.67 x 10-8 W/m·K4

21. Ejemplo 3: Una superficie Encuentre
esférica de 12 cm de radio se potencia
calienta a 627 0C. La emisividad radiada
es 0.12. ¿Qué potencia se radia?
A  4 R 2  4 (0.12 m) 2 A
A = 0.181 m2
T = 627 + 273; T = 900 K
6270C
P  es AT 4
P  (0.12)(5.67 x 10 W/mK )(0.181 m )(900 K)
-8 4 2 4
Potencia radiada desde la
P = 808 W
superficie:

22. Resumen: Transferencia de calor
Conducción: La energía térmica se
transfiere mediante colisiones
moleculares adyacentes dentro de un
material. El medio en sí no se mueve.
Convección es el proceso por el que
la energía térmica se transfiere
mediante el movimiento masivo real
de un fluido calentado.
Radiación es el proceso por el que la
energía térmica se transfiere
mediante ondas electromagnéticas.

23. Resumen de conductividad térmica
La conductividad térmica k de un t1 t2
material es una medida de su
habilidad para conducir calor.
H = corriente calorífica (J/s)
A = área superficial (m2)
Dt = diferencia de temperatura Dt = t2 - t1
L = espesor del material
kADt
Q QL
H  k Unidades 
J
 L A Dt s  m  C

24. Resumen de radiación
La tasa de radiación R es la energía emitida por unidad de
área por unidad de tiempo (potencia por unidad de área).
Rate of Radiation R  Q  P P
R   es T 4
(W/m2):
R A A A
Emisividad, e : 0>e >1
Constante de Stefan-Boltzman:
s = 5.67 x 10-8 W/m·K4

25. Resumen de fórmulas
Q kADt QL
H  k Unidades 
J
 L A Dt s  m  C
Q kADt H k Dt
H  ;  P  es AT 4
 L A L
Q P P
R  R   es T 4
A A A

26. CONCLUSIÓN:
Transferencia de calor