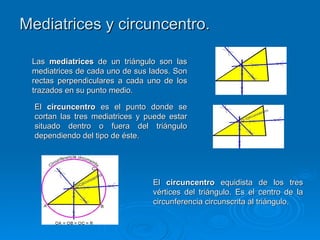
El documento describe diferentes elementos geométricos asociados a un triángulo, incluyendo las medianas, mediatrices, alturas, bisectrices y la recta de Euler. Explica que las medianas, bisectrices y alturas se cortan en el baricentro, incentro y ortocentro respectivamente, y que las mediatrices se cortan en el circuncentro. También define la recta de Euler como la recta que pasa por el baricentro, circuncentro y ortocentro de un triángulo.

1. T riángulo :
s
R e y P unto no s
ctas s table
R e as y Punt o
Rect
R e as y R
Rect
Rect
e

2. Medianas y Baricentro
Las medianas de un triángulo son los
segmentos que unen un vértice con el punto
medio del lado opuesto
El baricentro es el punto dónde se cortan
las tres medianas del triángulo y está
siempre situado en el interior del triángulo.
El baricentro divide a cada mediana en dos
segmentos, uno que doble el otro.

3. Mediatrices y circuncentro.
Las mediatrices de un triángulo son las
mediatrices de cada uno de sus lados. Son
rectas perpendiculares a cada uno de los
trazados en su punto medio.
El circuncentro es el punto donde se
cortan las tres mediatrices y puede estar
situado dentro o fuera del triángulo
dependiendo del tipo de éste.
El circuncentro equidista de los tres
vértices del triángulo. Es el centro de la
circunferencia circunscrita al triángulo.

4. Alturas y ortocentro.
Las alturas de un triángulo son los
segmentos perpendiculares trazados desde
cada vértice al lado opuesto
El ortocentro es el punto donde se cortan
las tres alturas de un triángulo. Puede estar
situado dentro o fuera del triángulo,
dependiendo del tipo de éste.

5. Bisectrices e incentro.
Las bisectrices de un triángulo son las
bisectrices de cada uno de sus ángulos. Son
las semirrectas que dividen al ángulo en dos
partes iguales y cuyo origen es el vértice del
ángulo.
El incentro es el punto donde se cortan las tres
bisectrices del triángulo y está siempre situado
en el interior del triángulo.
El incentro equidista de los tres lados del
triángulo. Es el centro de la circunferencia
inscrita al triángulo.

6. Recta de Euler
La recta de Euler
es la recta que pasa
por el baricentro, el
circuncentro, y el
ortocentro de un
triángulo.