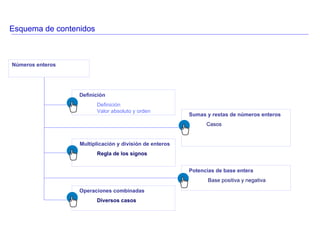
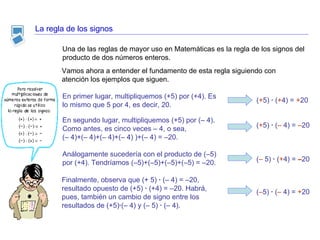
El documento presenta información sobre números enteros y operaciones matemáticas con ellos. Explica conceptos como suma, resta, multiplicación y división de números enteros, siguiendo la regla de los signos. Incluye ejemplos de cálculo de expresiones combinadas que involucran varias operaciones.

1. 5 Los números enteros La perinola o pirindola tiene seis lados, y es parecida a un trompo que se hace girar con los dedos corazón y pulgar hasta que se detiene. El jugador tiene que esperar a que se pare para obedecer la indicación de la cara que queda hacia arriba: Pon 1 – 1 Pon 2 – 2 Todos ponen Toma 1 +1 Toma 2 +2 Toma TODO Pirindola LECTURA INICIAL ESQUEMA

2. La matemática china Busca en la web Primera página de “Nueve Capitulos del Arte Matemático”, libro clave de la matemática china (siglo I). Enlace a un resumen. Enlace a cuadrados y círculos mágicos chinos

3. Esquema de contenidos Números enteros Definición Definición Valor absoluto y orden Sumas y restas de números enteros Casos Multiplicación y división de enteros Regla de los signos Operaciones combinadas Diversos casos Potencias de base entera Base positiva y negativa

4. Suma y resta de números enteros Al sumar o restar números enteros, has de fijarte en que los paréntesis que aparezcan se eliminan teniendo en cuenta el signo + ó – que les antecede. Se sigue la regla de los signos: el signo + conserva el signo del número que sigue, mientras que el signo – lo cambia . SIGUIENTE

5. Suma y resta de números enteros Al sumar o restar números enteros, has de fijarte en que los paréntesis que aparezcan se eliminan teniendo en cuenta el signo + ó – que les antecede. Se sigue la regla de los signos: el signo + conserva el signo del número que sigue, mientras que el signo – lo cambia . Simplifica las siguientes sumas y restas de enteros: SIGUIENTE

6. Suma y resta de números enteros Al sumar o restar números enteros, has de fijarte en que los paréntesis que aparezcan se eliminan teniendo en cuenta el signo + ó – que les antecede. Se sigue la regla de los signos: el signo + conserva el signo del número que sigue, mientras que el signo – lo cambia . Simplifica las siguientes sumas y restas de enteros: (+8) + (–3) = (+8) – (–3) = (+8) + (+3) = (+8) – (+3) = SIGUIENTE

7. Suma y resta de números enteros Al sumar o restar números enteros, has de fijarte en que los paréntesis que aparezcan se eliminan teniendo en cuenta el signo + ó – que les antecede. Se sigue la regla de los signos: el signo + conserva el signo del número que sigue, mientras que el signo – lo cambia . Simplifica las siguientes sumas y restas de enteros: 8 + 3 = 11 8 – 3 = 5 (+8) + (–3) = (+8) – (–3) = (+8) + (+3) = (+8) – (+3) = SIGUIENTE

8. Suma y resta de números enteros Al sumar o restar números enteros, has de fijarte en que los paréntesis que aparezcan se eliminan teniendo en cuenta el signo + ó – que le antecede. Se sigue la regla de los signos: el signo + conserva el signo del número que sigue, mientras que el signo – lo cambia . Simplifica las siguientes sumas y restas de enteros: 8 + 3 = 11 8 – 3 = 5 (+8) + (–3) = (+8) – (–3) = 8 – 3 = 5 8 + 3 = 11 (+8) + (+3) = (+8) – (+3) = SIGUIENTE

9. Suma y resta de números enteros Al sumar o restar números enteros, has de fijarte en que los paréntesis que aparezcan se eliminan teniendo en cuenta el signo + ó – que le antecede. Se sigue la regla de los signos: el signo + conserva el signo del número que sigue, mientras que el signo – lo cambia . Simplifica las siguientes sumas y restas de enteros: 8 + 3 = 11 8 – 3 = 5 (+8) + (–3) = (+8) – (–3) = 8 – 3 = 5 8 + 3 = 11 (–7) + (–5) = (–7) – (–5) = (+8) + (+3) = (+8) – (+3) = (–7) + (+5) = (–7) – (+5) = SIGUIENTE

10. Suma y resta de números enteros Al sumar o restar números enteros, has de fijarte en que los paréntesis que aparezcan se eliminan teniendo en cuenta el signo + ó – que le antecede. Se sigue la regla de los signos: el signo + conserva el signo del número que sigue, mientras que el signo – lo cambia . Simplifica las siguientes sumas y restas de enteros: 8 + 3 = 11 8 – 3 = 5 (+8) + (–3) = (+8) – (–3) = 8 – 3 = 5 8 + 3 = 11 (–7) + (–5) = (–7) – (–5) = – 7 + 5 = –2 – 7 – 5 = –12 (+8) + (+3) = (+8) – (+3) = (–7) + (+5) = (–7) – (+5) = SIGUIENTE

11. Suma y resta de números enteros Al sumar o restar números enteros, has de fijarte en que los paréntesis que aparezcan se eliminan teniendo en cuenta el signo + ó – que le antecede. Se sigue la regla de los signos: el signo + conserva el signo del número que sigue, mientras que el signo – lo cambia . Simplifica las siguientes sumas y restas de enteros: 8 + 3 = 11 8 – 3 = 5 (+8) + (–3) = (+8) – (–3) = 8 – 3 = 5 8 + 3 = 11 (–7) + (–5) = (–7) – (–5) = – 7 + 5 = –2 – 7 – 5 = –12 – 7 – 5 = –12 – 7 + 5 = –2 (+8) + (+3) = (+8) – (+3) = (–7) + (+5) = (–7) – (+5) =

12. La regla de los signos Una de las reglas de mayor uso en Matemáticas es la regla de los signos del producto de dos números enteros. Vamos ahora a entender el fundamento de esta regla siguiendo con atención los ejemplos que siguen. SIGUIENTE

13. La regla de los signos En primer lugar, multipliquemos (+5) por (+4). Es lo mismo que 5 por 4, es decir, 20. (+5) · (+4) = +20 Una de las reglas de mayor uso en Matemáticas es la regla de los signos del producto de dos números enteros. Vamos ahora a entender el fundamento de esta regla siguiendo con atención los ejemplos que siguen. SIGUIENTE

14. La regla de los signos En segundo lugar, multipliquemos (+5) por (– 4). Como antes, es cinco veces – 4, o sea, (– 4)+(– 4)+(– 4)+(– 4) )+(– 4) = –20. (+5) · (– 4) = –20 Una de las reglas de mayor uso en Matemáticas es la regla de los signos del producto de dos números enteros. Vamos ahora a entender el fundamento de esta regla siguiendo con atención los ejemplos que siguen. En primer lugar, multipliquemos (+5) por (+4). Es lo mismo que 5 por 4, es decir, 20. (+5) · (+4) = +20 SIGUIENTE

15. La regla de los signos Una de las reglas de mayor uso en Matemáticas es la regla de los signos del producto de dos números enteros. Vamos ahora a entender el fundamento de esta regla siguiendo con atención los ejemplos que siguen. Análogamente sucedería con el producto de (– 5) por (+4). Tendríamos (–5)+(–5)+(–5)+(–5) = –20. (–5) · (+4) = –20 SIGUIENTE En primer lugar, multipliquemos (+5) por (+4). Es lo mismo que 5 por 4, es decir, 20. (+5) · (+4) = +20 En segundo lugar, multipliquemos (+5) por (– 4). Como antes, es cinco veces – 4, o sea, (– 4)+(– 4)+(– 4)+(– 4) )+(– 4) = –20. (+5) · (– 4) = –20

16. La regla de los signos Una de las reglas de mayor uso en Matemáticas es la regla de los signos del producto de dos números enteros. Vamos ahora a entender el fundamento de esta regla siguiendo con atención los ejemplos que siguen. En primer lugar, multipliquemos (+5) por (+4). Es lo mismo que 5 por 4, es decir, 20. ( + 5) · ( + 4) = + 20 En segundo lugar, multipliquemos (+5) por (– 4). Como antes, es cinco veces – 4, o sea, (– 4)+(– 4)+(– 4)+(– 4) )+(– 4) = –20. ( + 5) · ( – 4) = – 20 Análogamente sucedería con el producto de (–5) por (+4). Tendríamos (–5)+(–5)+(–5)+(–5) = –20. ( – 5) · ( + 4) = – 20 Finalmente, observa que (+ 5) · (– 4) = –20, resultado opuesto de (+5) · (+4) = –20. Habrá, pues, también un cambio de signo entre los resultados de (+5) · (– 4) y (– 5) · (– 4). ( – 5) · ( – 4) = + 20

17. Operaciones combinadas Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. SIGUIENTE

18. Operaciones combinadas Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. Calcula el valor simplificado de la expresión: (+30) : [(– 4) + (+9)] – (– 5) · (+3) + (– 4) = SIGUIENTE

19. Operaciones combinadas Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. Calcula el valor simplificado de la expresión: (+30) : [(– 4) + (+9)] – (– 5) · (+3) + (– 4) = = (+30) : (+ 5) – (– 5) · (+3) + (– 4) = SIGUIENTE

20. Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. Calcula el valor simplificado de la expresión: = (+ 6) – (– 15) + (– 4) = (+30) : [(– 4) + (+9)] – (– 5) · (+3) + (– 4) = = (+30) : (+ 5) – (– 5) · (+3) + (– 4) = Operaciones combinadas SIGUIENTE

21. Operaciones combinadas Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. Calcula el valor simplificado de la expresión: = 6 + 15 – 4 = = (+ 6) – (– 15) + (– 4) = (+30) : [(– 4) + (+9)] – (– 5) · (+3) + (– 4) = = (+30) : (+ 5) – (– 5) · (+3) + (– 4) = SIGUIENTE

22. Operaciones combinadas Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. Calcula el valor simplificado de la expresión: 17 = 6 + 15 – 4 = = (+ 6) – (– 15) + (– 4) = (+30) : [(– 4) + (+9)] – (– 5) · (+3) + (– 4) = = (+30) : (+ 5) – (– 5) · (+3) + (– 4) = SIGUIENTE

23. Operaciones combinadas Es importante también traducir a lenguaje matemático instrucciones de cálculo como las siguientes: a) A – 9 le restas el producto de 3 por – 5 y le sumas el triple de – 2. b) Al resultado de dividir 10 entre – 5, lo multiplicas por la suma de – 6 y 11. Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. SIGUIENTE

24. Operaciones combinadas Es importante también traducir a lenguaje matemático instrucciones de cálculo como las siguientes: a) A – 9 le restas el producto de 3 por – 5 y le sumas el triple de – 2. b) Al resultado de dividir 10 entre –5, lo multiplicas por la suma de –6 y 11. (–9) – 3 · (– 5) + 3 ·(–2) = Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. SIGUIENTE

25. Operaciones combinadas Es importante también traducir a lenguaje matemático instrucciones de cálculo como las siguientes: a) A –9 le restas el producto de 3 por – 5 y le sumas el triple de – 2. b) Al resultado de dividir 10 entre – 5, lo multiplicas por la suma de – 6 y 11. Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. (– 9) – 3 · (– 5) + 3 ·(–2) = (– 9) – (–15) + 3 · (– 2) = SIGUIENTE

26. Operaciones combinadas Es importante también traducir a lenguaje matemático instrucciones de cálculo como las siguientes: a) A –9 le restas el producto de 3 por –5 y le sumas el triple de –2. b) Al resultado de dividir 10 entre – 5, lo multiplicas por la suma de – 6 y 11. Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. – 9 + 15 – 6 = 0 (–9) – 3 · (– 5) + 3 ·(–2) = (–9) – (–15) + 3 · (–2) = SIGUIENTE

27. Operaciones combinadas Es importante también traducir a lenguaje matemático instrucciones de cálculo como las siguientes: a) A –9 le restas el producto de 3 por – 5 y le sumas el triple de – 2. b) Al resultado de dividir 10 entre – 5, lo multiplicas por la suma de – 6 y 11. [(10) : (–5)] · [(– 6) + 11] = Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. – 9 + 15 – 6 = 0 SIGUIENTE (– 9) – 3 · (– 5) + 3 ·(–2) = (– 9) – (–15) + 3 · (– 2) =

28. Operaciones combinadas Es importante también traducir a lenguaje matemático instrucciones de cálculo como las siguientes: a) A – 9 le restas el producto de 8 por – 5 y le sumas el triple de – 2. b) Al resultado de dividir 10 entre – 5, lo multiplicas por la suma de – 6 y 11. [(10) : (– 5)] · [(– 6) + 11] = (– 2) · (+ 5) Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. – 9 + 15 – 6 = 0 SIGUIENTE (– 9) – 3 · (– 5) + 3 ·(–2) = (– 9) – (–15) + 3 · (– 2) =

29. Operaciones combinadas Es importante también traducir a lenguaje matemático instrucciones de cálculo como las siguientes: a) A – 9 le restas el producto de 8 por – 5 y le sumas el triple de – 2. b) Al resultado de dividir 10 entre – 5, lo multiplicas por la suma de – 6 y 11. [(10) : (– 5)] · [(– 6) + 11] = (– 2) · (+ 5) = –10 – 9 + 15 – 6 = 0 Las expresiones combinadas de enteros con las operaciones de sumar, restar, multiplicar y dividir son calculables correctamente si se sigue la jerarquía de signos que ya conoces. (– 9) – 3 · (– 5) + 3 ·(–2) = (– 9) – (–15) + 3 · (– 2) =

30. Potencias de base entera Si a n es una potencia cuya base es un número entero, positivo o negativo, puede ocurrir que su resultado sea también positivo o negativo. Es negativo si la base es negativa y el exponente es impar . Es positivo en todos los demás casos . ¡Cuidado!: No confundas (–2) 4 con – 2 4 , pues (–2) 4 es: (–2) · (–2) · (–2) · (–2)= + 16 , y, en cambio, – 2 4 es: – 2 · 2 · 2 · 2 = – 16 . SIGUIENTE

31. Potencias de base entera Si a n es una potencia cuya base es un número entero, positivo o negativo, puede ocurrir que su resultado sea también positivo o negativo. Es negativo si la base es negativa y el exponente es impar . Es positivo en todos los demás casos . ¡Cuidado!, no confundas (–2) 4 con – 2 4 , pues (–2) 4 es: (–2) · (–2) · (–2) · (–2)= + 16 , y, en cambio, – 2 4 es: – 2 · 2 · 2 · 2 = – 16 . Relaciona los valores de la primera fila con los que son iguales a ellos en la segunda fila (hazlo empezando por la izquierda): – 81 – 32 – 1 1 32 81 5 – 5 – 2 5 (– 2) 5 – 3 4 (– 3) 4 – 1 44 (–1) 44 (– 5) 0 – 5 0 SIGUIENTE

32. Potencias de base entera Si a n es una potencia cuya base es un número entero, positivo o negativo, puede ocurrir que su resultado sea también positivo o negativo. Es negativo si la base es negativa y el exponente es impar . Es positivo en todos los demás casos . ¡Cuidado!, no confundas (–2) 4 con – 2 4 , pues (–2) 4 es: (–2) · (–2) · (–2) · (–2)= + 16 , y, en cambio, – 2 4 es: – 2 · 2 · 2 · 2 = – 16 . Relaciona los valores de la primera fila con los que son iguales a ellos en la segunda fila (hazlo empezando por la izquierda): – 2 5 (– 2) 5 – 3 4 (– 3) 4 – 1 44 (– 1) 44 – 81 – 32 1 32 81 (– 5) 0 – 5 0 5 – 5 – 1 SIGUIENTE

33. Potencias de base entera Si a n es una potencia cuya base es un número entero, positivo o negativo, puede ocurrir que su resultado sea también positivo o negativo. Es negativo si la base es negativa y el exponente es impar . Es positivo en todos los demás casos . ¡Cuidado!, no confundas (–2) 4 con –2 4 , pues (–2) 4 es: (–2) · (–2) · (–2) · (–2)= + 16 , y, en cambio, –2 4 es: – 2 · 2 · 2 · 2 = – 16 . Relaciona los valores de la primera fila con los que son iguales a ellos en la segunda fila (hazlo empezando por la izquierda): – 81 – 32 1 32 81 5 – 5 – 2 5 (– 2) 5 – 3 4 (– 3) 4 – 1 44 (–1) 44 (– 5) 0 – 5 0 – 1 SIGUIENTE

34. Potencias de base entera Si a n es una potencia cuya base es un número entero, positivo o negativo, puede ocurrir que su resultado sea también positivo o negativo. Es negativo si la base es negativa y el exponente es impar . Es positivo en todos los demás casos . ¡Cuidado!, no confundas (–2) 4 con –2 4 , pues (–2) 4 es: (–2) · (–2) · (–2) · (–2)= + 16 , y, en cambio, –2 4 es: – 2 · 2 · 2 · 2 = – 16 . Relaciona los valores de la primera fila con los que son iguales a ellos en la segunda fila (hazlo empezando por la izquierda): – 81 – 32 – 1 1 32 81 5 – 5 – 2 5 (– 2) 5 – 3 4 (– 3) 4 – 1 44 (–1) 44 (– 5) 0 – 5 0 SIGUIENTE

35. Potencias de base entera Si a n es una potencia cuya base es un número entero, positivo o negativo, puede ocurrir que su resultado sea también positivo o negativo. Es negativo si la base es negativa y el exponente es impar . Es positivo en todos los demás casos . ¡Cuidado!, no confundas (–2) 4 con –2 4 , pues (–2) 4 es: (–2) · (–2) · (–2) · (–2)= + 16 , y, en cambio, –2 4 es: – 2 · 2 · 2 · 2 = – 16 . Relaciona los valores de la primera fila con los que son iguales a ellos en la segunda fila (hazlo empezando por la izquierda): – 81 – 32 – 1 1 32 81 5 – 5 – 2 5 (– 2) 5 – 3 4 (– 3) 4 – 1 44 (–1) 44 (– 5) 0 – 5 0 SIGUIENTE

36. Potencias de base entera Si a n es una potencia cuya base es un número entero, positivo o negativo, puede ocurrir que su resultado sea también positivo o negativo. Es negativo si la base es negativa y el exponente es impar . Es positivo en todos los demás casos . ¡Cuidado!, no confundas (–2) 4 con –2 4 , pues (–2) 4 es: (–2) · (–2) · (–2) · (–2)= + 16 , y, en cambio, –2 4 es: – 2 · 2 · 2 · 2 = – 16 . Relaciona los valores de la primera fila con los que son iguales a ellos en la segunda fila (hazlo empezando por la izquierda): – 81 – 32 – 1 1 32 81 5 – 5 – 2 5 (– 2) 5 – 3 4 (– 3) 4 – 1 44 (–1) 44 (– 5) 0 – 5 0 SIGUIENTE

37. Potencias de base entera Si a n es una potencia cuya base es un número entero, positivo o negativo, puede ocurrir que su resultado sea también positivo o negativo. Es negativo si la base es negativa y el exponente es impar . Es positivo en todos los demás casos . ¡Cuidado!, no confundas (– 2) 4 con – 2 4 , pues (– 2) 4 es: (–2) · (–2) · (–2) · (–2)= + 16 , y, en cambio, – 2 4 es: – 2 · 2 · 2 · 2 = – 16 . Relaciona los valores de la primera fila con los que son iguales a ellos en la segunda fila (hazlo empezando por la izquierda): – 81 – 32 – 1 1 32 81 5 – 5 – 2 5 (– 2) 5 – 3 4 (– 3) 4 – 1 44 (–1) 44 (– 5) 0 – 5 0 SIGUIENTE

38. Potencias de base entera Si a n es una potencia cuya base es un número entero, positivo o negativo, puede ocurrir que su resultado sea también positivo o negativo. Es negativo si la base es negativa y el exponente es impar . Es positivo en todos los demás casos . ¡Cuidado!, no confundas (–2) 4 con –2 4 , pues (–2) 4 es: (–2) · (–2) · (–2) · (–2)= + 16 , y, en cambio, –2 4 es: – 2 · 2 · 2 · 2 = – 16 . Relaciona los valores de la primera fila con los que son iguales a ellos en la segunda fila (hazlo empezando por la izquierda): – 81 – 32 – 1 1 32 81 5 – 5 – 2 5 (– 2) 5 – 3 4 (– 3) 4 – 1 44 (–1) 44 (– 5) 0 – 5 0 SIGUIENTE

39. Potencias de base entera Si a n es una potencia cuya base es un número entero, positivo o negativo, puede ocurrir que su resultado sea también positivo o negativo. Es negativo si la base es negativa y el exponente es impar . Es positivo en todos los demás casos . ¡Cuidado!, no confundas (–2) 4 con – 2 4 , pues (– 2) 4 es: (–2) · (–2) · (–2) · (–2)= + 16 , y, en cambio, – 2 4 es: – 2 · 2 · 2 · 2 = – 16 . Relaciona los valores de la primera fila con los que son iguales a ellos en la segunda fila (hazlo empezando por la izquierda): – 81 – 32 – 1 1 32 81 5 – 5 – 2 5 (– 2) 5 – 3 4 (– 3) 4 – 1 44 (–1) 44 (– 5) 0 – 5 0