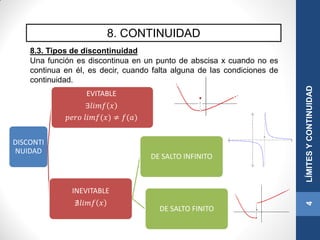
Este documento trata sobre los conceptos de límites y continuidad en matemáticas. Introduce las funciones reales de variable real, el concepto formal de límite, los límites infinitos y en el infinito, las propiedades de los límites y diferentes métodos para calcular límites, incluyendo las indeterminaciones. Finalmente, explica el concepto de continuidad y el teorema de Bolzano.

1. UD 4: LÍMITES Y
CONTINUIDAD
PROF: ALFONSO NAVARRO
MATEMÁTICAS II

2. ÍNDICE
1. FUNCIONES REALES DE VARIABLE REAL
2. CONCEPTO DE LÍMITE
3. LÍMITES INFINITOS
4. PROPIEDADES DE LOS LÍMITES
5. CÁLCULO DE LÍMITES
6. INDETERMINACIONES
7. INFINITÉSIMOS
8. CONTINUIDAD
9. TEOREMA DE BOLZANO

3. 1. FUNCIONES REALES DE VARIABLE REAL
1.1. Concepto de función
Se define función real de variable real, y se denota con la letra “f”, a
toda aplicación que a cada número real “x”, le asigna un único
número real “y”:
𝑓: 𝐷 ⊂ ℝ → ℝ
𝑥 → 𝑦 = 𝑓(𝑥)
4LÍMITESYCONTINUIDAD
Es función No es función

4. 1. FUNCIONES REALES DE VARIABLE REAL
Dominio
El dominio de la función es el conjunto 𝐷 ⊂ ℝ de los valores para los
que está definida la función. Se representa por Dom f.
𝐷𝑜𝑚 𝑓 = 𝑥 ∈ ℝ /𝑓 𝑥 𝑒𝑥𝑖𝑠𝑡𝑒
Imagen
El recorrido o imagen de la función es el conjunto de valores que
toma la función. Se representa por Im f.
𝐼𝑚 𝑓 = 𝑦 ∈ ℝ /𝑦 = 𝑓 𝑥 , 𝑥 ∈ 𝐷𝑜𝑚(𝑓)
4LÍMITESYCONTINUIDAD
Ejemplo. 𝑦 = 𝑥2 − 9

5. 1. FUNCIONES REALES DE VARIABLE REAL
1.2. Tipos de funciones y su dominio
4LÍMITESYCONTINUIDAD

6. 2. CONCEPTO DE LÍMITE
2.1. Idea intuitiva
La expresión, lim
𝑥→𝑎
𝑓 𝑥 = 𝑏 ,que se lee: “el límite
de f(x) cuando x tiende a “a” es b”, indica el
valor que toma la función cuando tomamos
valores muy próximos a “a”.
4LÍMITESYCONTINUIDAD
lim
𝑥→4
𝑥2 − 2𝑥 = 8
Ejemplo

7. 2. CONCEPTO DE LÍMITE
2.2. Definición matemática
4LÍMITESYCONTINUIDAD
lim
𝑥→𝑥 𝑜
𝑓 𝑥 = 𝐿 ⇔ ∀ℇ > 0, ∃𝛿 > 0/ si 0 < 𝑥 − 𝑥0 < 𝛿 ⟹ 𝑓 𝑥 − 𝐿 < ℇ

8. 2. CONCEPTO DE LÍMITE
2.3. Límites laterales
Para que ocurra que lim
𝑥→𝑎
𝑓 𝑥 = 𝑏 , se tiene que cumplir que cuando
tomamos valores de x próximos a “a”, tanto por la izquierda como por
la derecha, éstos coincidan. Llamamos límites laterales a estos
límites.
4LÍMITESYCONTINUIDAD

9. 2. CONCEPTO DE LÍMITE
4LÍMITESYCONTINUIDAD
Ejemplo. Calcula:
lim
𝑥→−2
𝑓(𝑥)
lim
𝑥→−1
𝑓(𝑥)
lim
𝑥→1
𝑓(𝑥)

10. 3. LÍMITES INFINITOS
3.1. Límites infinitos
La expresión 𝐥𝐢𝐦
𝒙→𝒂
𝒇 𝒙 = ±∞ , que se lee “el límite de f(x) cuando x
tiende a “a” es más/menos infinito”, quiere decir que a medida que
nos acercamos al valor “a” tanto por la izquierda como por la derecha
la variable dependiente de hace cada vez infinitamente
mayores/menores (según si es + o – infinito).
4LÍMITESYCONTINUIDAD
Ejemplo.

11. 3. LÍMITES INFINITOS
Asíntota vertical
Cuando ocurre que lim
𝑥→𝑎
𝑓 𝑥 = ±∞ decimos que la función presenta
una asíntota vertical, siendo la ecuación de la misma x = a.
4LÍMITESYCONTINUIDAD
Ejemplos.

12. 3. LÍMITES INFINITOS
3.2. Límites en el infinito
La expresión 𝐥𝐢𝐦
𝒙→±∞
𝒇 𝒙 = 𝒃 , que se lee “el límite de f(x) cuando x
tiende a ±∞ es b”, quiere decir que a medida que la variable
independiente (x) tiende a un valor muy grande/pequeño, la función
se acerca cada vez más a un valor “b” (pudiendo ser o no infinito, tal
y como mostramos en los ejemplos).
4LÍMITESYCONTINUIDAD
Ejemplos.

13. 3. LÍMITES INFINITOS
Asíntota horizontal
Cuando ocurre que lim
𝑥→±∞
𝑓 𝑥 = 𝑏 , donde 𝑏 ∈ ℝ, decimos que la
función presenta una asíntota horizontal, siendo la ecuación de la
misma y = b.
4LÍMITESYCONTINUIDAD
Ejemplos.

14. 4. PROPIEDADES DE LOS LÍMITES
4.1. Propiedades de los límites
1. Unicidad. El límite en caso de existir es único.
2. Sean lim
𝑥→𝑎
𝑓 𝑥 = 𝑏1 y lim
𝑥→𝑎
𝑓 𝑥 = 𝑏2 donde 𝑏1, 𝑏2 ∈ ℝ entonces se
cumple que:
3. Si existe lim
𝑥→𝑎
𝑓 𝑥 donde a ∈ ℝ entonces se cumple que:
4LÍMITESYCONTINUIDAD

15. 4. PROPIEDADES DE LOS LÍMITES
4LÍMITESYCONTINUIDAD

16. 5. CÁLCULO DE LÍMITES
5.1. Límites sencillos
Para determinar el valor de lim
𝑥→𝑎
𝑓 𝑥 , se sustituye la variable por el
valor al que tiende. Existen ocasiones en las que no se puede
determinar de manera inmediata este valor al tratarse de una
indeterminación.
4LÍMITESYCONTINUIDAD
Ejercicio. Calcula los siguiente límites:

17. 5. CÁLCULO DE LÍMITES
5.2. Indeterminaciones
4LÍMITESYCONTINUIDAD
INDETERMINACIONES RESOLUCIÓN
𝑘
0
𝑑𝑜𝑛𝑑𝑒 𝑘𝜖ℝ
Estudiar los límites laterales y ver si coinciden.
∞
∞
Comparar el grado del polinomio numerador y
denominador (dividiendo).
∞ − ∞
Hacer operaciones con ambas funciones «f(x)-g(x)» y
simplificar.
0 · ∞
Suelen resolverse operando y simplificando «f(x)·g(x)».
0
0
Factorizar los polinomios numerador y denominador y
simplificar. En caso de existir raíces multiplicar con el
conjugado.
1∞
Tomar logaritmos o aplicar la «fórmula» para simplificar el
límite según la definición del número e.

18. 5. CÁLCULO DE LÍMITES
4LÍMITESYCONTINUIDAD
𝑰𝒏𝒅𝒆𝒕𝒆𝒓𝒎𝒊𝒏𝒂𝒄𝒊ó𝒏
𝒌
𝟎
𝑎) lim
𝑥→5
𝑥
0
Ejercicios
𝑏) lim
𝑥→−1
𝑥 − 1
𝑥 + 1

19. 5. CÁLCULO DE LÍMITES
4LÍMITESYCONTINUIDAD
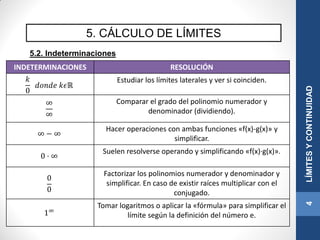
𝑰𝒏𝒅𝒆𝒕𝒆𝒓𝒎𝒊𝒏𝒂𝒄𝒊ó𝒏
∞
∞
Habitualmente se trata de un cociente de polinomios donde la variable
independiente tiende a infinito.
lim
𝑥→∞
𝑃 𝑥 = ∞
lim
𝑥→∞
𝑄 𝑥 = ∞
Luego: lim
𝑥→∞
𝑃(𝑥)
𝑄(𝑥)
=
∞
∞
que es una indeterminación.
CASO 1 gr[P(x)] > gr[Q(x)]
lim
𝑥→∞
𝑃(𝑥)
𝑄(𝑥)
= ±∞
CASO 2 g[P(x)] = gr[Q(x)]
lim
𝑥→∞
𝑃(𝑥)
𝑄(𝑥)
= 𝐾
CASO 3 gr[P(x)] < gr[Q(x)]
lim
𝑥→∞
𝑃(𝑥)
𝑄(𝑥)
= 0

20. 5. CÁLCULO DE LÍMITES
4LÍMITESYCONTINUIDAD
𝑰𝒏𝒅𝒆𝒕𝒆𝒓𝒎𝒊𝒏𝒂𝒄𝒊ó𝒏
∞
∞
𝑎) lim
𝑥→∞
3𝑥3 + 2𝑥 − 3
𝑥2 − 1
𝑏) lim
𝑥→∞
𝑥2
+ 𝑥 − 12
−2𝑥2 − 1
𝑐) lim
𝑥→∞
𝑥 + 1
𝑥2 + 𝑥 + 3
Ejercicios
𝑑) lim
𝑥→3
1
𝑥2 − 9
−
1
𝑥 − 3

21. 5. CÁLCULO DE LÍMITES
4LÍMITESYCONTINUIDAD
Ejercicio resuelto
lim
𝑥→3
1
𝑥2 − 9
−
1
𝑥 − 3
lim
𝑥→3
1
𝑥2 − 9
−
1
𝑥 − 3
= ∞ − ∞ 𝐼𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎𝑐𝑖ó𝑛
lim
𝑥→3
1
𝑥2 − 9
−
1
𝑥 − 3
= lim
𝑥→3
−𝑥 − 2
(𝑥 + 3)(𝑥 − 3)
=
−5
0
𝐸𝑠𝑡𝑢𝑑𝑖𝑎𝑚𝑜𝑠 𝑙í𝑚𝑖𝑡𝑒𝑠 𝑙𝑎𝑡.
lim
𝑥→3−
−𝑥 − 2
(𝑥 + 3)(𝑥 − 3)
= +∞
lim
𝑥→3+
−𝑥 − 2
(𝑥 + 3)(𝑥 − 3)
= −∞
𝐶𝑜𝑚𝑜 𝑛𝑜 𝑐𝑜𝑖𝑛𝑐𝑖𝑑𝑒𝑛
𝑛𝑜 𝑒𝑥𝑖𝑠𝑡𝑒 𝑒𝑙 𝑙í𝑚𝑖𝑡𝑒

22. 5. CÁLCULO DE LÍMITES
4LÍMITESYCONTINUIDAD
𝑓 𝑥 =
−𝑥 − 2
(𝑥 + 3)(𝑥 − 3)

23. 5. CÁLCULO DE LÍMITES
4LÍMITESYCONTINUIDAD
𝑰𝒏𝒅𝒆𝒕𝒆𝒓𝒎𝒊𝒏𝒂𝒄𝒊ó𝒏 ∞ − ∞
Hacer operaciones con ambas funciones «f(x)-g(x)» y simplificar.
Ejercicios
𝑎) lim
𝑥→−∞
3𝑥2 − 2
𝑥
+
5 − 𝑥2
𝑥 − 1
𝑏) lim
𝑥→+∞
2𝑥 − 1 − 3𝑥

24. 5. CÁLCULO DE LÍMITES
4LÍMITESYCONTINUIDAD
𝑰𝒏𝒅𝒆𝒕𝒆𝒓𝒎𝒊𝒏𝒂𝒄𝒊ó𝒏 𝟎 · ∞
Suelen resolverse operando y simplificando «f(x)·g(x)».
Ejercicios
𝑎) lim
𝑥→3
(𝑥2
+ 6𝑥 + 9)
1
𝑥 + 3
𝑏) lim
𝑥→2
(𝑥 − 2)
1
𝑥2 − 𝑥 − 2

25. 5. CÁLCULO DE LÍMITES
4LÍMITESYCONTINUIDAD
𝑰𝒏𝒅𝒆𝒕𝒆𝒓𝒎𝒊𝒏𝒂𝒄𝒊ó𝒏
𝟎
𝟎
Factorizar los polinomios numerador y denominador y simplificar.
En caso de existir raíces multiplicar con el conjugado.
Ejercicios
𝑎) lim
𝑥→0
3 − 𝑥 + 9
𝑥
𝑏) lim
𝑥→2
(𝑥 + 2)(3𝑥 − 2)
(𝑥 + 1)(𝑥 + 2)
𝑐) lim
𝑥→3
𝑥3 − 4𝑥2 − 3𝑥 + 18
𝑥3 − 5𝑥2 + 3𝑥 + 9

26. 5. CÁLCULO DE LÍMITES
4LÍMITESYCONTINUIDAD
𝑰𝒏𝒅𝒆𝒕𝒆𝒓𝒎𝒊𝒏𝒂𝒄𝒊ó𝒏 𝟏∞
Se produce en límites de la siguiente forma:
𝐿 = lim
𝑥→∞
𝑓(𝑥) 𝑔(𝑥)
𝑑𝑜𝑛𝑑𝑒 𝑓 𝑥 → 1 𝑦 𝑔 𝑥 → ∞
Para resolver podemos aplicar los siguiente métodos:
1. Expresión: 𝐿 = 𝑒lim 𝑥→∞ 𝑔 𝑥 [𝑓 𝑥 −1]
2. Tomar logaritmos neperianos.
3. Empleando la definición del número e como límite de la
sucesión:
𝑒 = lim
𝑥→∞
1 +
1
𝑓(𝑥)
𝑓(𝑥)

27. 5. CÁLCULO DE LÍMITES
4LÍMITESYCONTINUIDAD
𝑰𝒏𝒅𝒆𝒕𝒆𝒓𝒎𝒊𝒏𝒂𝒄𝒊ó𝒏 𝟏∞
Ejemplos:
lim
𝑥→∞
2𝑥 + 1
2𝑥 − 2
2𝑥+1

28. 7. INFINITÉSIMOS
7.1. Concepto
Decimos que una función y=f(x) es un infinitésimos en x=a si se
verifica que:
lim
𝑥→𝑎
𝑓 𝑥 = 0
4LÍMITESYCONTINUIDAD

29. 8. CONTINUIDAD
8.1. Continuidad de una función de un punto
Una función f(x) es continua es un punto, de abcisa «a», si se
cumple las tres condiciones siguientes:
1. ∃ lim
𝑥→𝑎
𝑓 𝑥
2. ∃ 𝑓 𝑎
3. 𝑓 𝑎 = lim
𝑥→𝑎
𝑓 𝑥
4LÍMITESYCONTINUIDAD

30. 8. CONTINUIDAD
8.2. Continuidad de una función en un intervalo
Una función f(x) es continua en un intervalo abierto (a,b) cuando lo
es en cada uno de sus puntos.
Una función f(x) es continua en un intervalo cerrado [a,b] cuando
lo es en cada uno de sus puntos del correspondiente intervalo abierto
(a,b) y, además, es continua por la derecha en a y por la izquierda en
b.
4LÍMITESYCONTINUIDAD

31. 8. CONTINUIDAD
8.3. Tipos de discontinuidad
Una función es discontinua en un punto de abscisa x cuando no es
continua en él, es decir, cuando falta alguna de las condiciones de
continuidad.
4LÍMITESYCONTINUIDAD
DISCONTI
NUIDAD
EVITABLE
∃𝑙𝑖𝑚𝑓 𝑥
𝑝𝑒𝑟𝑜 𝑙𝑖𝑚𝑓(𝑥) ≠ 𝑓(𝑎)
INEVITABLE
∄𝑙𝑖𝑚𝑓 𝑥
DE SALTO INFINITO
DE SALTO FINITO

32. 8. CONTINUIDAD
Ejercicios
4LÍMITESYCONTINUIDAD
Estudia la continuidad de las siguientes funciones a partir de su
gráfica:

33. 8. CONTINUIDAD
Ejercicios
4LÍMITESYCONTINUIDAD
Estudia la continuidad de las siguientes funciones a partir de su
gráfica:

34. 8. CONTINUIDAD
Ejercicios
4LÍMITESYCONTINUIDAD
Estudia la continuidad de las siguientes funciones:

35. 9. TEOREMA DE BOLZANO
9.1 Enunciado
Sea una función f real que cumple las siguiente dos condiciones:
1. f es continua en un intervalo cerrado [a, b]
2. Signo f(a) ≠ f(b)
Entonces se cumple que existe un punto 𝑐 ∈ (𝑎, 𝑏)/𝑓 𝑐 = 0
4LÍMITESYCONTINUIDAD

36. 9. TEOREMA DE BOLZANO
4LÍMITESYCONTINUIDAD

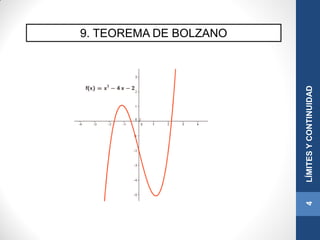
37. 9. TEOREMA DE BOLZANO
Ejemplo
Probar que la ecuación x3 - 4x - 2 = 0 tiene alguna raíz real,
aproximando su valor hasta las décimas.
Consideramos la función f(x) = x3 - 4x - 2 la cual es continua por
ser polinómica.
Tanteando, tenemos que f(2) = - 2 y f(3) = 13
Es decir, tenemos una función continua en el intervalo [2,
3] donde signo de f(2) ≠ signo de f(3) .
Por lo tanto, por el Teorema de Bolzano, existe un c ∈ [2, 3] tal
que f(c) = 0 .
Para aproximar la solución a la décima seguimos tanteando:
f(2,2) = - 0,152 y f(2,3) = 0,967
Tememos una función continua en el
intervalo [2,2;2,3] donde signo de f(2,2) ≠ signo de f(2,3) .
Es decir, existe un c ∈ [2,2, 2,3] tal que f(c) = 0 .
4LÍMITESYCONTINUIDAD

38. 9. TEOREMA DE BOLZANO
4LÍMITESYCONTINUIDAD