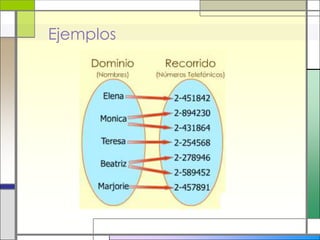
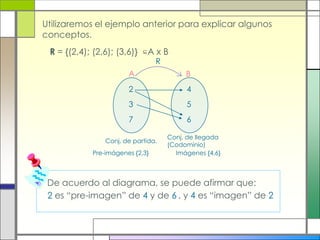
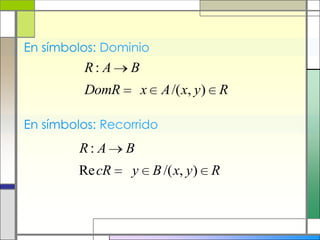
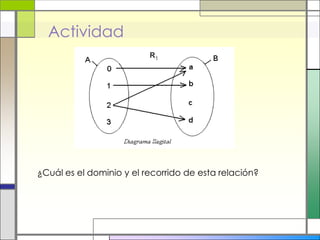
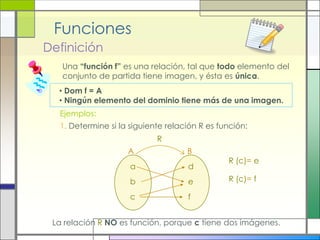
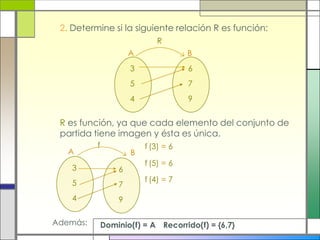
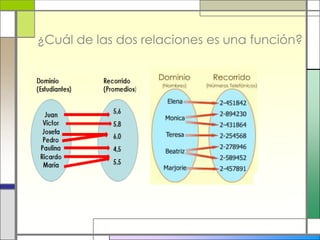
Este documento describe las relaciones y funciones. Explica que una relación es una correspondencia entre dos conjuntos llamados dominio y recorrido, donde cada elemento del dominio corresponde a uno o más elementos del recorrido. Una función es una relación especial donde cada elemento del dominio tiene una única imagen en el recorrido. También define conceptos como dominio, recorrido, pre-imagen e imagen. Finalmente, presenta ejemplos para ilustrar estas definiciones.

1. Relaciones y Funciones

2. Objetivo
□ Comprender el concepto de relación

3. Ejemplos
□ En un almacén, a cada artículo le
corresponde un precio.
□ A cada nombre del directorio telefónico le
corresponde uno o varios números.
□ A cada número le corresponde una
segunda potencia.
□ A cada estudiante le corresponde un
promedio de calificaciones

4. Definición 1:
□ Relación es la correspondencia de un
primer conjunto, llamado Dominio, con un
segundo conjunto, llamado Recorrido, de
manera que a cada elemento del Dominio
le corresponde uno o más elemento del
Recorrido o Rango.

5. Ejemplos
Dominio Recorrido
(Estudiantes) (Promedios)
5,6
Juan
Víctor 5,8
Josefa
6,0
Pedro
Paulina 4,5
Ricardo
5,5
María

6. Ejemplos

7. Producto Cartesiano
Dados los conjuntos A y B , su producto cartesiano
(A×B) está formado por cada uno de los pares
ordenados donde el primer elemento pertenece a A
y el segundo a B:
A x B = { (a,b) / a Є A y b Є B }
Ejemplo:
Si A = { a, b, c } y B = { 1, 2 } , entonces:
A x B = { (a,1), (a,2), (b,1), (b,2), (c,1), (c,2)}

8. Definición:
Una “relación R” de un conjunto A a un conjunto B
(R: A B), es un subconjunto del producto
cartesiano entre A y B (A x B), determinado por una,
o más condiciones.
Ejemplo:
Si A = {2, 3, 7} y B = {4, 5, 6} y R una relación de A en
B tal que:
R = { (a,b) Є A x B / b es múltiplo de a}
entonces:
A x B = {(2,4); (2,5); (2,6); (3,4); (3,5); (3,6); (7,4); (7,5); (7,6)}
R = {(2,4); (2,6); (3,6)} AxB

9. El par (2,4) pertenece a la relación R, ya que 4 es
múltiplo de 2.
Los pares (2,6) y (3,6), también están relacionados, ya
que
6 es múltiplo de 2 y de 3.
Notación: (2,4) Є R ó 2R4 ó R (2) = 4
(2,6) Є R ó 2R6 ó R (2) = 6
(3,6) Є R ó 3R6 ó R (3) = 6

11. Utilizaremos el ejemplo anterior para explicar algunos
conceptos.
R = {(2,4); (2,6); (3,6)} AxB
R
A B
2 4
3 5
7 6
Conj. de llegada
Conj. de partida.
(Codominio)
Pre-imágenes {2,3} Imágenes {4,6}
De acuerdo al diagrama, se puede afirmar que:
2 es “pre-imagen” de 4 y de 6 , y 4 es “imagen” de 2

12. Dominio y Recorrido
Dominio:
Es el conjunto formado por todos los elementos del
conjunto de partida que son pre-imagen de algún
elemento del conjunto de llegada.
Recorrido:
Es el conjunto formado por todos los elementos del
conjunto de llegada que son imagen de algún
elemento del conjunto de partida.
Ejemplo:
Si A = {2, 3, 7} y B = {4, 5, 6} y R una relación de A en
B tal que:
R = {(2,4); (2,6); (3,6)} A x B , entonces:
Dom(R): = {2,3}
Rec(R): = {4,6}

13. En símbolos: Dominio
R: A B
DomR x A /( x, y) R
En símbolos: Recorrido
R: A B
Re cR y B /( x, y) R

14. Ejemplos
1) R (2,3), (5, 7), (1, 1), (3, 4)
DomR 2,5,1,3
2) S ( José , María), ( Sebastián, Elena), ( Romeo, Julieta)
DomS José , Sebastián, Romeo

15. Ejemplos
1) R (2,3), (5, 7), (1, 1), (3, 4)
Re cR 3, 7, 1, 4
2) S ( José , María), ( Sebastián, Elena), ( Romeo, Julieta)
Re cS María, Elena, Julieta

16. Actividad
¿Cuál es el dominio y el recorrido de esta relación?

17. Funciones

18. □ Objetivo: Comprender el concepto de
función

19. Funciones
Definición
Una “función f” es una relación, tal que todo elemento del
conjunto de partida tiene imagen, y ésta es única.
• Dom f = A
• Ningún elemento del dominio tiene más de una imagen.
Ejemplos:
1. Determine si la siguiente relación R es función:
R
A B
R (c)= e
a d
b e R (c)= f
c f
La relación R NO es función, porque c tiene dos imágenes.

20. 2. Determine si la siguiente relación R es función:
R
A B
3 6
5 7
4 9
R es función, ya que cada elemento del conjunto de
partida tiene imagen y ésta es única.
f f (3) = 6
A B
f (5) = 6
3 6
5 f (4) = 7
7
4 9
Además: Dominio(f) = A Recorrido(f) = {6,7}

21. ¿Cuál de las dos relaciones es una función?