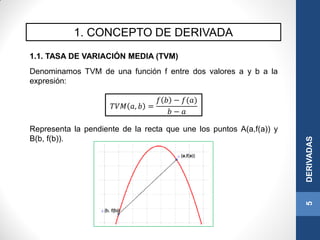
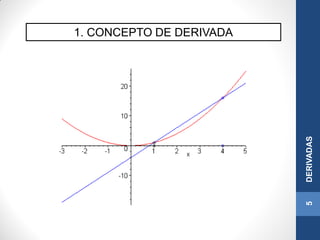
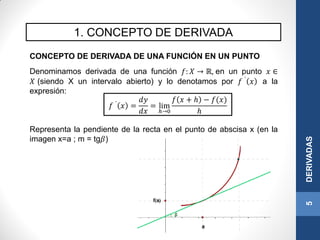
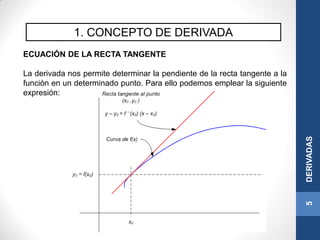
Este documento presenta conceptos sobre derivadas. Introduce el concepto de derivada como la pendiente de la recta tangente a una función en un punto. Explica que una función es derivable si es continua y sus derivadas laterales son iguales. Además, incluye reglas para calcular derivadas como la derivada de sumas, productos y funciones compuestas, así como derivadas de funciones elementales como exponenciales, logarítmicas y potencias.







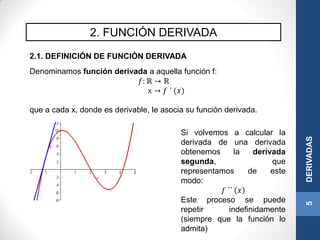





![2. FUNCIÓN DERIVADA
5DERIVADAS
2.2. REGLAS DE DERIVACIÓN
1.DERIVADA DE UNA CONSTANTE 𝑓 𝑥 = 𝐾 → 𝑓´ 𝑥 = 0, 𝑐𝑜𝑛 𝐾 ∈ ℝ
2. DERIVADA DE PRODUCTO POR
CONSTANTE
𝑓 𝐾 · 𝑥 ´ = 𝐾 · 𝑓´ 𝑥 , 𝑐𝑜𝑛 𝐾 ∈ ℝ
3. DERIVADA DE LA SUMA/RESTA 𝑓 ± 𝑔 ´ 𝑥 = 𝑓´ 𝑥 ± 𝑔´(𝑥)
4. DERIVADA DE UNA PRODUCTO 𝑓 · 𝑔 ´ 𝑥 = 𝑓´ 𝑥 𝑔 𝑥 + 𝑓 𝑥 · 𝑔´(𝑥)
5. DERIVADA DE UNA COCIENTE
𝑓
𝑔
´ 𝑥 =
𝑓´ 𝑥 𝑔 𝑥 − 𝑓 𝑥 · 𝑔´(𝑥)
[𝑔 𝑥 ]2
6. DERIVADA DE LA COMPOSICIÓN 𝑓 𝑔 𝑥 ´ = 𝑓 ´ 𝑔 𝑥 · 𝑔´(𝑥)](https://image.slidesharecdn.com/ud5derivadas-171116174743/85/Ud-5-derivadas-19-320.jpg)

![2. FUNCIÓN DERIVADA
5DERIVADAS
2.3. DERIVADA DE LA FUNCIÓN INVERSA
La función inversa de la función 𝑓 es otra que de denota 𝑓−1 y que
cumple que:
𝑓 ∘ 𝑓−1
𝑥 = 𝑥 ; 𝑓−1
∘ 𝑓 𝑥 = 𝑥
Se cumple entonces que:
𝑓−1 ´ 𝑥 =
1
𝑓 ´ (𝑓−1 𝑥 )
EJEMPLOS
a) y = 𝑥𝑛
→
Su inversa es 𝑦−1
= 𝑥 𝑛
, ya que
y ∘ 𝑦−1
= x ó y 𝑦−1
x = x, derivando esta expresión:
[ 𝑥𝑛 𝑛
]´ = 1 → n · 𝑥𝑛 𝑛−1
𝑥𝑛
´ = 1 → 𝑥𝑛
´ =
1
𝑛 𝑥 𝑛−1𝑛
b) y = 2𝑥5
+ 3𝑥 − 1](https://image.slidesharecdn.com/ud5derivadas-171116174743/85/Ud-5-derivadas-21-320.jpg)





