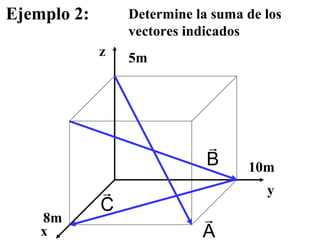
Este documento describe diferentes tipos de magnitudes físicas como escalares y vectoriales, y conceptos básicos de vectores como suma, resta, multiplicación por escalar y producto escalar y vectorial. Explica cómo representar vectores mediante componentes rectangulares y coordenadas polares, y cómo determinar la magnitud y dirección de la suma de varios vectores.

1. C 2C 2 MAGNITUDES FÍSICAS.MAGNITUDES FÍSICAS.
• Magnitudes fMagnitudes fíísicas escalares ysicas escalares y
vectoriales. Algebra vectorial.vectoriales. Algebra vectorial.
•EjemplosEjemplos
Bibliog. Sears, FBibliog. Sears, Física universitaria 1999,ísica universitaria 1999,
Hewitt, Física conceptual 1999Hewitt, Física conceptual 1999

2. MagnitudesMagnitudes
físicasfísicas
por su naturaleza
Escalares
Vectoriales

3. MagnitudesMagnitudes
físicasfísicas
Escalares
Vectoriales
Asociadas a propiedades que pueden ser
caracterizadas a través de una cantidad
Asociadas a propiedades que se caracterizan
no sólo por su cantidad sino por su dirección
y su sentido

4. MagnitudesMagnitudes
físicasfísicas
Masa, densidad,
temperatura, energía,
trabajo, etc
Velocidad, fuerza,
cantidad de movimiento,
aceleración, torque, etc.
Escalares
Vectoriales

5. SR: Cuerpos que se toman como referencia para
describir el movimiento del sistema bajo estudio.
Bases para el estudio delBases para el estudio del
movimiento mecánicomovimiento mecánico
x(t)x(t)
y(t)y(t)
z(t)z(t)
Se le asociaSe le asocia
• ObservadorObservador
• Sistema deSistema de
CoordenadasCoordenadas
y
x
z
• RelojReloj

6. Movimiento planoMovimiento plano
Coordenadas Cartesianas
y (m)
x (m)
O
origen
abcisa
ordenada (x,y)
Q (-2,2)
P (8,3)

7. Coordenadas Polares
O
origen
(r,θ)
θ
Movimiento planoMovimiento plano

8. Relacion entre (x,y) y (r,θ)
y (m)
x (m)
O
origen
abcisa
ordenada
(x,y)
θ
r
θcosrx =
θrseny =
θtan=
x
y22
yxr +=

9. VectoresVectores
Notación A
Módulo A > 0
A
Dirección ϕθ,
x
y
z
θ
ϕ
Ap
ϕ
x
y

10. PropiedadesPropiedades
de Vectoresde Vectores
• Dados A y B, si A = B entonces A = B
• Todo vector se puede desplazar paralelamente a
si mismo
A

B

C

CBA

==

11. Suma deSuma de
VectoresVectores
B
A
R
B
A C
C
Ley del polígono

12. El vector resultante es
aquel que vector que va
desde el origen del primer
vector hasta el extremo del
ultimo

13. A

B

C

D

Entonces si se tiene los
siguientes vectores
El vector resultante
de la suma de todos
ellos será:

14. A
 B

C

D

DCBAR

+++=
R


15. PropiedadesPropiedades
de Vectoresde Vectores
A
Opuesto
-A
Nulo 0 = A + ( )-A
Vector unitario A
A


=μ
µ
µ= ˆAA


16. PropiedadesPropiedades
de la suma dede la suma de
VectoresVectores
Ley
Conmutativa
ABBAR +=+=
Ley Asociativa
C)BA)CBAR

++=++= ((
Diferencia
B-AR

=
)B(-AR

+=
A
B A
-B
R

17. Ley conmutativa
¿Como se explica esta regla?
Los vectores A y B pueden ser
desplazados paralelamente para
encontrar el vector suma
B
R
=
A+B
A
B R
=
B+A
(Método paralelogramo)
B R
=
A+B

18. Multiplicación de un vector por un
escalar
Dado dos vectores ByA

Se dicen que son paralelos si BA

α=
BAsi

↑↑> 0α
BAsi

↑↓< 0α
BAsi

==1α

19. A

B

AB

2
1
=
A

B

AB

4
1
−=

20. Ejemplo 8:
Hallar el vector resultante de la suma de los
siguientes vectores
A B
C
A B
CR = 2

21. Vectores unitarios en el plano
iˆjˆ
x
y
iˆ Vector unitario en la dirección del eje x+
jˆ Vector unitario en la dirección del eje y+

22. Vectores unitarios en el espacio
x
y
z
iˆ
jˆ
kˆ

23. RepresentaciónRepresentación
de un vectorde un vector
x
y
z
θ
ϕ
A
Ax
Ay
Az
θsenAAx ϕcos=
θsenAsenAy ϕ=
θcosAAz =
222
zyx AAAAA ++==

kAjAiAA zyx

++=

24. Observaciones:
Las componentes rectangulares de
un vector dependen del sistema
coordenado elegido.
La magnitud del vector no cambia.
Permanece invariante en cualquier
sistema coordenado

25. Determínese la resultante de los
siguientes vectores
+
A

4u 3u
B

BAR

+=
7u

26. +
A

B

8u 4u =
BAR

+=
4u

27. Observamos que, cuando los vectores
están en la misma dirección podemos
determinar fácilmente su magnitud
¿Que sucede si los vectores no están en
la misma dirección ? , ¿ podremos
determinar directamente su magnitud ?

28. 4u
3u
A

B

La magnitud en este caso no puede determinarse
directamente , por lo que debemos tratar de
buscar otra forma de determinarla
BAR

+=

29. A

B

yA

xA

xB

yB

4u
3u
5u
6u
8u
10u

30. yA

xA

xB

yB

4u
3u
6u
8u
yx AAA

+=
yx BBB

+=

31. yy BA

+
xx BA

+
10u
5u
yyxx BABAR

+++=
Por pitagoras podemos ahora determinar la
magnitud del vector resultante uR 55510 22
=+=

32. yA

x
A

xB

yB

xC
y
C

xD

y
D


33. yyyyy
DCBAR

+++=
xxxxx
DCBAR

+++=
x
R

y
R

15 u
5 u
yx
RRR

+=
105R =

34. x
y
z
(x1,y1,z1)
(x2,y2,z2)
A

Dados los puntos
indicados el vector que
los une esta
representado por

35. x
y
z
(x1,y1,z1)
(x2,y2,z2)
A

k)z(zj)y(yi)x(xA 121212
ˆˆˆ −+−+−=


36. ProductoProducto
escalar de dosescalar de dos
vectoresvectores
θABBA cos=⋅

cosθAAB =
Proyección de A sobre B
cosθBBA =
Proyección de B sobre A

37. 1ˆˆ =⋅ii
1ˆˆ =⋅ jj
0ˆˆ =⋅ ji
0ˆˆ =⋅kj
0ˆˆ =⋅ki
xAiA =⋅ ˆ

1ˆˆ =⋅kk
yAjA =⋅ ˆ

zAkA =⋅ ˆ

ZZYYXX BABABABA ++=⋅


38. ProductoProducto
vectorial de dosvectorial de dos
vectoresvectores BAC

×=
θABC sen=
0iˆiˆ

=× 0ˆˆ

=× jj
0ˆˆ

=×kk
kji ˆˆˆ =× ikj ˆˆˆ =×
jik ˆˆˆ =×

39. )kˆBjˆBiˆB()kˆAjˆAiˆA(BAC zyxzyx ++×++=×=

YZZYX BABAC −=
zxxzy BABAC −=
xyyxz BABAC −=
Demostrar:

40. Determinese la suma de los siguientes vectores:
Ejemplo 1:
k5j8i3A ˆˆˆ ++=

kji-5B ˆ3ˆ2ˆ −+=

kji4C ˆ2ˆ7ˆ −−=


41. Ejemplo 2:
8m
10m
5m
A

B

C

Determine la suma de los
vectores indicados
x
y
z

42. Ejemplo 9
Dados los vectores:
kˆ3jˆ5iˆ4B
kˆ5jˆ3iˆ3A
−+=
−+=


Determine :
a) El producto escalar entre ellos.
b)el producto vectorial entre ambos
e) el ángulo que forman entre sí.
Tarea 9c, 9d y 10