Torsion
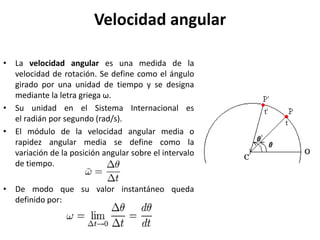
- 1. Velocidad angular La velocidad angular es una medida de la velocidad de rotación. Se define como el ángulo girado por una unidad de tiempo y se designa mediante la letra griega ω. Su unidad en el Sistema Internacional es el radián por segundo (rad/s). El módulo de la velocidad angular media o rapidez angular media se define como la variación de la posición angular sobre el intervalo de tiempo. De modo que su valor instantáneo queda definido por:
- 2. Aceleración angular Se define la aceleración angular como el cambio que experimenta la velocidad angularpor unidad de tiempo. Se denota por la letra griega alfa α. Al igual que la velocidad angular, la aceleración angular tiene carácter vectorial. Se expresa en radianes por segundo al cuadrado, o s-2, ya que el radián es adimensional.
- 3. Par o momento de torsión En mecánica newtoniana, se denomina momento de una fuerzaa una magnitud obtenida como producto vectorial del vector de posición del punto de aplicación de la fuerza con respecto al origen y el vector de fuerza. Ocasionalmente recibe el nombre de torque a partir del término inglés (torque), derivado a su vez del latín torquere (retorcer). Su símbolo debe escribirse como N m o N•m N·m parece equivaler al julio, sin embargo, el momento de fuerza es una magnitud vectorial, mientras que la energía es una magnitud escalar.
- 4. Calculo de momentos en el plano Si se considera una fuerza aplicada en un punto P del plano de trabajo y otro punto O sobre el mismo plano, el módulo del momento en O viene dado por: Siendo el módulo de la fuerza, el brazo de momento, es decir, la distanciaa la que se encuentra el punto O (en el que tomamos momento) de la recta de aplicación de la fuerza, y el suplementario del ángulo que forman los dos vectores.
- 5. Trabajo en el movimiento de rotación Considérese un cuerpo rígido que puede girar alrededor de un eje fijo tal como se indica en la figura. Supongamos que se aplica una fuerza exterior F en el punto P. El trabajo realizado por dicha fuerza a medida que el cuerpo gira recorriendo una distancia infinitesimal ds=rdθ en el tiempo dt es F·senφ es la componente tangencial de la fuerza, la componente de la fuerza a lo largo del desplazamiento. La componente radial de la fuerza no realiza trabajo, ya que es perpendicular al desplazamiento. El momento de la fuerza es el producto de la componente tangencial de la fuerza por el radio. La expresión del trabajo la podemos escribir de forma alternativa
- 6. Potencia angular La potencia angular es el trabajo angular sobre tiempo El trabajo angular es proporcional a velocidad angular, y se relacionan de esta manera: es la potencia (en W) es el par motor (en N·m) es la velocidad angular (en rad/s)
