Exámenes corregidos de termodinámica pensados para 1º de Bachillerato.

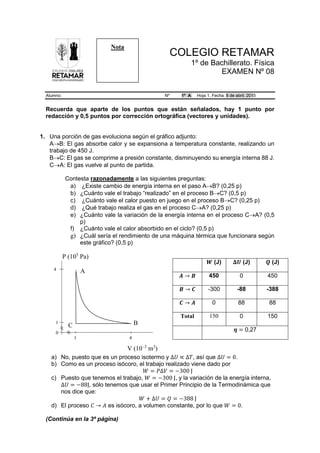
1. COLEGIO RETAMAR
1º de Bachillerato. Física
EXAMEN Nº 08
Alumno: Nº 1º A Hoja 1. Fecha: 8 de abril, 2015
Recuerda que aparte de los puntos que están señalados, hay 1 punto por
redacción y 0,5 puntos por corrección ortográfica (vectores y unidades).
1. Una porción de gas evoluciona según el gráfico adjunto:
A→B: El gas absorbe calor y se expansiona a temperatura constante, realizando un
trabajo de 450 J.
B→C: El gas se comprime a presión constante, disminuyendo su energía interna 88 J.
C→A: El gas vuelve al punto de partida.
Contesta razonadamente a las siguientes preguntas:
a) ¿Existe cambio de energía interna en el paso A→B? (0,25 p)
b) ¿Cuánto vale el trabajo “realizado” en el proceso B→C? (0,5 p)
c) ¿Cuánto vale el calor puesto en juego en el proceso B→C? (0,25 p)
d) ¿Qué trabajo realiza el gas en el proceso C→A? (0,25 p)
e) ¿Cuánto vale la variación de la energía interna en el proceso C→A? (0,5
p)
f) ¿Cuánto vale el calor absorbido en el ciclo? (0,5 p)
g) ¿Cuál sería el rendimiento de una máquina térmica que funcionara según
este gráfico? (0,5 p)
a) No, puesto que es un proceso isotermo y Δ𝑈𝑈 ∝ Δ𝑇𝑇, así que Δ𝑈𝑈 = 0.
b) Como es un proceso isócoro, el trabajo realizado viene dado por
𝑊𝑊 = 𝑃𝑃Δ𝑉𝑉 = −300 J
c) Puesto que tenemos el trabajo, 𝑊𝑊 = −300 J, y la variación de la energía interna,
Δ𝑈𝑈 = −88J, sólo tenemos que usar el Primer Principio de la Termodinámica que
nos dice que:
𝑊𝑊 + Δ𝑈𝑈 = 𝑄𝑄 = −388 J
d) El proceso 𝐶𝐶 → 𝐴𝐴 es isócoro, a volumen constante, por lo que 𝑊𝑊 = 0.
(Continúa en la 3ª página)
𝑾𝑾 (J) 𝚫𝚫𝑼𝑼 (J) 𝑸𝑸 (J)
𝑨𝑨 → 𝑩𝑩 450 0 450
𝑩𝑩 → 𝑪𝑪 -300 -88 -388
𝑪𝑪 → 𝑨𝑨 0 88 88
Total 150 0 150
𝜼𝜼 = 0,27
Nota
V (10–3
m3
)
P (105
Pa)
C
A
B
1 4
0
1
4

2. 2. Indica si las siguientes afirmaciones son verdaderas (V) o Falsas (F). En caso de
que no sean ciertas, indica por qué. (La no argumentación supone un 0 inmediato).
(4 p.)
F
En un proceso isóbaro no se realiza trabajo alguno.
Eso ocurre si el proceso es isócoro, si es isóbaro el trabajo es 𝑊𝑊 = 𝑃𝑃Δ𝑉𝑉.
F
En los gases ideales se cumple que 𝒄𝒄𝑽𝑽 > 𝒄𝒄𝑷𝑷.
Como 𝑐𝑐𝑃𝑃 − 𝑐𝑐𝑉𝑉 = 𝑅𝑅 tenemos que, necesariamente 𝑐𝑐𝑃𝑃 > 𝑐𝑐𝑉𝑉.
F
El trabajo es una función de estado, porque únicamente depende de los
estados inicial y final.
El trabajo nunca puede ser una función de estado, aunque a veces se pueda calcular
a partir de funciones de estado, puesto que depende del proceso.
V
En una máquina térmica que realice un ciclo la variación de la energía interna
es cero.
F
En un sistema cerrado el calor intercambiado con el exterior es cero.
Lo que es cero es la materia intercambiada con el entorno.
V
El 2º principio de la termodinámica habla de la dirección de los procesos
espontáneos.
V
Ante una misma cantidad de calor agregado, la variación de la temperatura
en una sustancia será mayor cuanto menor sea el calor específico de dicha
sustancia.
F
En un gas ideal, la temperatura está relacionada con el intercambio de
momento lineal entre las partículas del gas y las paredes que lo contienen.
La temperatura está relacionada con la energía cinética media.
3. Se construye una máquina térmica que funciona según el esquema adjunto.
¿Contradice dicha máquina el Primer Principio de la Termodinámica? (1 p.)¿Y el
Segundo? (0,75 p.) Razona adecuadamente la respuesta.
No cumple el Primer Principio porque la energía no se conserva. Es decir, al sistema
entran 100 J, pero en forma de trabajo y calor salen únicamente 95 J.
Para que se cumpla el Segundo Principio debe cumplirse que Δ𝑆𝑆 ≥ 0. Para comprobar
esto vamos a calcular la entropía total.
La variación de entropía de la máquina vamos a suponerla nula (nosotros suponemos
todos los procesos de los que hablamos reversibles y, al ser la entropía función de
estado, y la máquina cíclica, Δ𝑆𝑆𝑚𝑚𝑚𝑚𝑚𝑚 = 0).
La variación de entropía de cada uno de los focos térmicos vamos a calcularla como
Δ𝑆𝑆𝑖𝑖 =
𝑄𝑄𝑖𝑖
𝑇𝑇𝑖𝑖
Así, para el foco 1 tenemos que
Δ𝑆𝑆1 =
𝑄𝑄1
𝑇𝑇1
= −
100J
400K
= −0,25 J/K
Y para el foco 2:
Δ𝑆𝑆2 =
𝑄𝑄2
𝑇𝑇2
=
75J
200K
= 0,375 J/K
Por tanto, Δ𝑆𝑆𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = Δ𝑆𝑆𝑚𝑚𝑚𝑚𝑚𝑚 + Δ𝑆𝑆1 + Δ𝑆𝑆2 = 0,125J
Y el 2º Principio sí que se conserva.
W = 20 J
Q1 = 100 J Q2 = 75 J
T1=400K
T2=200K

3. (Continuación de la pregunta 1).
e) La variación de la energía interna en el proceso 𝐶𝐶 → 𝐴𝐴 debe ser tal que la
variación total de la energía interna sea cero, puesto que es un ciclo. Así que:
Δ𝑈𝑈𝐶𝐶→𝐴𝐴 = 88 J
f) Según nuestro criterio de signos, el calor absorbido en el ciclo es la suma de
todos los procesos donde éste sea positivo, es decir:
𝑄𝑄𝑎𝑎𝑎𝑎𝑎𝑎 = 538 J
g) La eficiencia, también llamada rendimiento, viene dado por el cociente entre el
trabajo realizado por el ciclo y el calor que se le ha debido suministrar, es decir:
𝜂𝜂 =
𝑊𝑊𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐
𝑄𝑄𝑎𝑎𝑎𝑎𝑎𝑎
= 0,27

4. COLEGIO RETAMAR
1º de Bachillerato. Física
EXAMEN Nº 08
Alumno: Nº 1º B Hoja 1. Fecha: 8 de abril, 2015
Recuerda que aparte de los puntos que están señalados, hay 1 punto por
redacción y 0,5 puntos por corrección ortográfica (vectores y unidades).
1. Indica si las siguientes afirmaciones son verdaderas (V) o Falsas (F). En caso de
que no sean ciertas, indica por qué. (La no argumentación supone un 0 inmediato).
(4 p.)
F
En un proceso isóbaro el trabajo depende del 𝐥𝐥 𝐥𝐥(𝑽𝑽𝟐𝟐/𝑽𝑽𝟏𝟏).
En un proceso isóbaro el trabajo es directamente proporcional a la variación del
volumen. 𝑊𝑊 = 𝑃𝑃Δ𝑉𝑉.
V
En los gases ideales la diferencia entre 𝒄𝒄𝒑𝒑 y 𝒄𝒄𝒗𝒗 es de, aproximadamente,
𝟐𝟐 𝐜𝐜𝐜𝐜𝐜𝐜/ 𝐊𝐊 𝐦𝐦𝐦𝐦𝐦𝐦.
(Puesto que 𝑐𝑐𝑝𝑝 − 𝑐𝑐𝑣𝑣 = 𝑅𝑅 = 1,987 cal/K · mol)
V
La entalpía es una función de estado.
V
En un ciclo la variación de la entropía es cero.
(Porque la entropía, Δ𝑆𝑆, es una función de estado)
F
En un sistema cerrado el calor intercambiado con el exterior es cero.
En un sistema cerrado sí que hay intercambio de calor; de lo que no hay intercambio
es de materia.
V
El 2º principio de la termodinámica habla de la relación entre entropía e
irreversibilidad.
F
Ante una misma cantidad de calor agregado, la variación de la temperatura
en una sustancia será mayor cuanto mayor sea el calor específico de dicha
sustancia.
Cuanto mayor sea el calor específico, menor será la variación de temperatura.
F
En un gas ideal las partículas se aceleran entre dos colisiones consecutivas.
Entre una y otra colisión el momento lineal se conserva, y, como no hay
intercambio de masa (el choque es perfectamente elástico), la velocidad debe ser
la misma.
Nota

5. 2. Una máquina térmica, que contiene 2 moles de cierto gas ideal (𝒄𝒄𝒗𝒗 = 𝟑𝟑/𝟐𝟐 𝑹𝑹), a una
presión inicial de 𝑷𝑷𝑨𝑨 = 𝟏𝟏𝟏𝟏𝟒𝟒
𝐏𝐏𝐏𝐏 y un volumen 𝑽𝑽𝑨𝑨 = 𝟐𝟐𝟐𝟐𝟐𝟐 𝐋𝐋, realiza el siguiente ciclo.
i. Calienta el gas mediante un proceso isócoro hasta que su temperatura
se duplica.
ii. Después, se expanden manteniendo constante la temperatura.
iii. Finalmente, vuelven al estado inicial por medio de un proceso isóbaro.
a. Dibuja el diagrama 𝑷𝑷 − 𝑽𝑽. (0,5 p.)
b. Rellena la siguiente tabla de valores de (𝑷𝑷, 𝑽𝑽, 𝑻𝑻). (0,75 p.)
c. Calcula 𝑸𝑸, 𝑾𝑾, 𝜟𝜟𝜟𝜟 para todos los procesos del ciclo y rellena la tabla
correspondiente. (1,5 p.)
d. Calcula el rendimiento de la máquina. (0,5 p.)
e. Calcula el calor expelido (0,75 p.)
f. Calcula el trabajo realizado por la máquina (0,5 p.)
Para la realización de este problema vamos a necesitar la ecuación de estado de los
gases ideales, es decir:
𝑃𝑃𝑃𝑃 = 𝑛𝑛𝑛𝑛𝑛𝑛 (1),
donde 𝑅𝑅 = 8,314 J/Kmol. Y el Primer Principio de la Termodinámica:
𝑄𝑄 = 𝛥𝛥𝛥𝛥 + 𝑊𝑊 (2)
Utilizando la Ec. (1), podemos calcular la temperatura en A, que queda
𝑇𝑇𝐴𝐴 =
𝑃𝑃𝐴𝐴 𝑉𝑉𝐴𝐴
𝑛𝑛𝑛𝑛
= 120,3 K
El primer proceso, el 𝐴𝐴 → 𝐵𝐵, es isócoro, es decir
𝑉𝑉𝐴𝐴 = 𝑉𝑉𝐵𝐵 = 0,2 m3
(3)
Como la temperatura se duplica, tenemos que 𝑇𝑇𝐵𝐵 = 2𝑇𝑇𝐴𝐴 = 240,6 K.
Además, el proceso 𝐵𝐵 → 𝐶𝐶 es a temperatura constante, mientras que el 𝐶𝐶 → 𝐴𝐴 es a
presión constante, por lo que 𝑇𝑇𝐵𝐵 = 𝑇𝑇𝐶𝐶 y 𝑃𝑃𝐶𝐶 = 𝑃𝑃𝐴𝐴. Con esto, y con la Ec. (1), podemos
completar la tabla, tal y como la vemos más arriba.
Como la variación de la energía interna viene dado por:
𝑾𝑾 (J) 𝚫𝚫𝑼𝑼 (J) 𝑸𝑸 (J)
𝑨𝑨 → 𝑩𝑩 0 3 · 103
3 · 103
𝑩𝑩 → 𝑪𝑪 2773 0 2773
𝑪𝑪 → 𝑨𝑨 −2 · 103
−3 · 103
−5 · 103
Total 773 0 773
𝜼𝜼 = �
𝑊𝑊
𝑄𝑄𝑎𝑎𝑎𝑎𝑎𝑎
� = 0,13
𝑷𝑷 (Pa) 𝑽𝑽 (m3
) 𝑻𝑻 (K)
𝑨𝑨 𝟏𝟏𝟏𝟏𝟒𝟒 𝟎𝟎, 𝟐𝟐 120,3
𝑩𝑩 2 · 104 0,2 240,6
𝑪𝑪 104 0,4 240,6

6. Δ𝑈𝑈 = 𝑛𝑛𝑐𝑐𝑉𝑉Δ𝑇𝑇 (4)
Tenemos que para el proceso 𝐴𝐴 → 𝐵𝐵 la variación de la energía interna es Δ𝑈𝑈 = 3 kJ.
Como el proceso 𝐵𝐵 → 𝐶𝐶 es isotermo, en él Δ𝑈𝑈 = 0.
Y como la energía interna es una función de estado, la variación total de la energía
interna debe ser cero, por lo que Δ𝑈𝑈𝐶𝐶→𝐴𝐴 = −Δ𝑈𝑈𝐴𝐴→𝐵𝐵 = −3 kJ.
El trabajo, durante el proceso 𝐴𝐴 → 𝐵𝐵 es nulo, puesto que Δ𝑉𝑉 = 0 ↔ 𝑊𝑊 = 0 y, por lo
tanto, según el Primer Principio, Ec. (2), 𝑄𝑄 = Δ𝑈𝑈 = 3 kJ.
En el proceso 𝐵𝐵 → 𝐶𝐶 podemos hacer uso de que en un proceso isotermo
𝛥𝛥𝛥𝛥 = 0 ⇒ 𝛥𝛥𝛥𝛥 = 0 ⇒ 𝑄𝑄 = 𝑊𝑊 = 𝑛𝑛𝑛𝑛𝑛𝑛 𝑙𝑙𝑙𝑙 �
𝑉𝑉𝐶𝐶
𝑉𝑉𝐵𝐵
� (3)
Por lo tanto,
𝑊𝑊 = 2 mol · 8,314
J
Kmol
· 240,6 K · ln �
0,4
0,2
� = 2773 J
En el proceso 𝐶𝐶 → 𝐴𝐴 usamos que el trabajo para un proceso isóbaro es:
𝑊𝑊 = 𝑃𝑃Δ𝑉𝑉 = −2 kJ
La energía interna, en este caso, viene dada por:
Δ𝑈𝑈 = 𝑛𝑛𝑐𝑐𝑉𝑉Δ𝑇𝑇 = −3 kJ
Para terminar, usando el Primer Principio, llegamos a que:
𝑄𝑄 = 𝑊𝑊 + Δ𝑈𝑈 = −5 kJ
Finalmente, para calcular el rendimiento del ciclo debemos usar que éste es el cociente
entre el trabajo realizado por el ciclo (el trabajo total) y el calor absorbido por la máquina
(el calor suministrado), es decir:
𝜂𝜂 = �
𝑊𝑊
𝑄𝑄𝑎𝑎𝑎𝑎𝑎𝑎
� =
773
5773
= 0,13

7. COLEGIO RETAMAR
1º de Bachillerato. Física
EXAMEN Nº 08
Alumno: Nº 1º C Hoja 1. Fecha: 8 de abril, 2015
Recuerda que aparte de los puntos que están señalados, hay 1 punto por
redacción y 0,5 puntos por corrección ortográfica (vectores y unidades).
1. Indica si las siguientes afirmaciones son verdaderas (V) o Falsas (F). En caso de que
no sean ciertas, indica por qué. (La no argumentación supone un 0 inmediato). (4 p.)
F
En un proceso isotermo el calor transferido es 0.
Eso es en un proceso adiabático. En un proceso isotermo Δ𝑈𝑈 = 0.
F
En los gases ideales se cumple que 𝒄𝒄𝒗𝒗 < 𝒄𝒄𝒑𝒑.
Es al revés, 𝑐𝑐𝑣𝑣 < 𝑐𝑐_𝑝𝑝, puesto que 𝑐𝑐𝑝𝑝 − 𝑐𝑐𝑣𝑣 = 𝑅𝑅.
F
El trabajo es una función de estado, por que únicamente depende de los
estados inicial y final.
No es función de estado, por que depende del camino elegido.
V
En una máquina térmica que realice un ciclo la variación de la energía interna
es cero.
V
Un sistema aislado es siempre adiabático.
F
El 2º principio de la termodinámica rompe la equivalencia entre calor y trabajo.
El que hace eso es el Primer Principio.
F
Ante una misma cantidad de calor agregado, la variación de la temperatura
en una sustancia será menor cuanto menor sea el calor específico de dicha
sustancia.
La variación de temperatura será mayor cuanto menor sea el calor específico.
F
En un gas ideal, la temperatura está relacionada con el momento lineal medio
de las partículas.
Está relacionada con la energía cinética media.
Nota

8. 2. Una máquina térmica, que contiene 2 moles de cierto gas ideal (𝒄𝒄𝒗𝒗 =
𝟑𝟑/𝟐𝟐 𝑹𝑹), a una presión inicial de 𝑷𝑷𝑨𝑨 = 𝟏𝟏𝟏𝟏𝟒𝟒
𝐏𝐏𝐏𝐏 y un volumen 𝑽𝑽𝑨𝑨 = 𝟐𝟐𝟐𝟐𝟐𝟐 𝐋𝐋,
realiza el siguiente ciclo.
i. Los expande mediante un proceso isócoro hasta que su temperatura se
duplica.
ii. Después, se expanden manteniendo constante la temperatura.
iii. Finalmente, vuelven al estado inicial por medio de un proceso isóbaro.
a. Dibuja el diagrama 𝑷𝑷 − 𝑽𝑽. (0,5 p.)
b. Rellena la siguiente tabla de valores de (𝑷𝑷, 𝑽𝑽, 𝑻𝑻). (0,75 p.)
c. Calcula 𝑸𝑸, 𝑾𝑾, 𝜟𝜟𝜟𝜟 para todos los procesos del ciclo y rellena la tabla
correspondiente. (1,5 p.)
d. Calcula el rendimiento de la máquina. (0,5 p.)
e. Calcula el calor expelido (0,75 p.)
f. Calcula el trabajo realizado por la máquina (0,5 p.)
Para la realización de este problema vamos a necesitar la ecuación de estado de los
gases ideales, es decir:
𝑃𝑃𝑃𝑃 = 𝑛𝑛𝑛𝑛𝑛𝑛 (1),
donde 𝑅𝑅 = 8,314 J/Kmol. Y el Primer Principio de la Termodinámica:
𝑄𝑄 = 𝛥𝛥𝛥𝛥 + 𝑊𝑊 (2)
Utilizando la Ec. (1), podemos calcular la temperatura en A, que queda
𝑇𝑇𝐴𝐴 =
𝑃𝑃𝐴𝐴 𝑉𝑉𝐴𝐴
𝑛𝑛𝑛𝑛
= 120,3 K
El primer proceso, el 𝐴𝐴 → 𝐵𝐵, es isócoro, es decir
𝑉𝑉𝐴𝐴 = 𝑉𝑉𝐵𝐵 = 0,2 m3
(3)
Como la temperatura se duplica, tenemos que 𝑇𝑇𝐵𝐵 = 2𝑇𝑇𝐴𝐴 = 240,6 K.
Además, el proceso 𝐵𝐵 → 𝐶𝐶 es a temperatura constante, mientras que el 𝐶𝐶 → 𝐴𝐴 es a
presión constante, por lo que 𝑇𝑇𝐵𝐵 = 𝑇𝑇𝐶𝐶 y 𝑃𝑃𝐶𝐶 = 𝑃𝑃𝐴𝐴. Con esto, y con la Ec. (1), podemos
completar la tabla, tal y como la vemos más arriba.
Como la variación de la energía interna viene dado por:
𝑾𝑾 (J) 𝚫𝚫𝑼𝑼 (J) 𝑸𝑸 (J)
𝑨𝑨 → 𝑩𝑩 0 3 · 103
3 · 103
𝑩𝑩 → 𝑪𝑪 2773 0 2773
𝑪𝑪 → 𝑨𝑨 −2 · 103
−3 · 103
−5 · 103
Total 773 0 773
𝜼𝜼 = �
𝑊𝑊
𝑄𝑄𝑎𝑎𝑎𝑎𝑎𝑎
� = 0,13
𝑷𝑷 (Pa) 𝑽𝑽 (m3
) 𝑻𝑻 (K)
𝑨𝑨 𝟏𝟏𝟏𝟏𝟒𝟒 𝟎𝟎, 𝟐𝟐 120,3
𝑩𝑩 2 · 104 0,2 240,6
𝑪𝑪 104 0,4 240,6

9. Δ𝑈𝑈 = 𝑛𝑛𝑐𝑐𝑉𝑉Δ𝑇𝑇 (4)
Tenemos que para el proceso 𝐴𝐴 → 𝐵𝐵 la variación de la energía interna es Δ𝑈𝑈 = 3 kJ.
Como el proceso 𝐵𝐵 → 𝐶𝐶 es isotermo, en él Δ𝑈𝑈 = 0.
Y como la energía interna es una función de estado, la variación total de la energía
interna debe ser cero, por lo que Δ𝑈𝑈𝐶𝐶→𝐴𝐴 = −Δ𝑈𝑈𝐴𝐴→𝐵𝐵 = −3 kJ.
El trabajo, durante el proceso 𝐴𝐴 → 𝐵𝐵 es nulo, puesto que Δ𝑉𝑉 = 0 ↔ 𝑊𝑊 = 0 y, por lo
tanto, según el Primer Principio, Ec. (2), 𝑄𝑄 = Δ𝑈𝑈 = 3 kJ.
En el proceso 𝐵𝐵 → 𝐶𝐶 podemos hacer uso de que en un proceso isotermo
𝛥𝛥𝛥𝛥 = 0 ⇒ 𝛥𝛥𝛥𝛥 = 0 ⇒ 𝑄𝑄 = 𝑊𝑊 = 𝑛𝑛𝑛𝑛𝑛𝑛 𝑙𝑙𝑙𝑙 �
𝑉𝑉𝐶𝐶
𝑉𝑉𝐵𝐵
� (3)
Por lo tanto,
𝑊𝑊 = 2 mol · 8,314
J
Kmol
· 240,6 K · ln �
0,4
0,2
� = 2773 J
En el proceso 𝐶𝐶 → 𝐴𝐴 usamos que el trabajo para un proceso isóbaro es:
𝑊𝑊 = 𝑃𝑃Δ𝑉𝑉 = −2 kJ
La energía interna, en este caso, viene dada por:
Δ𝑈𝑈 = 𝑛𝑛𝑐𝑐𝑉𝑉Δ𝑇𝑇 = −3 kJ
Para terminar, usando el Primer Principio, llegamos a que:
𝑄𝑄 = 𝑊𝑊 + Δ𝑈𝑈 = −5 kJ
Finalmente, para calcular el rendimiento del ciclo debemos usar que éste es el cociente
entre el trabajo realizado por el ciclo (el trabajo total) y el calor absorbido por la máquina
(el calor suministrado), es decir:
𝜂𝜂 = �
𝑊𝑊
𝑄𝑄𝑎𝑎𝑎𝑎𝑎𝑎
� =
773
5773
= 0,13
El calor expelido viene dado por el calor calculado con signo negativo, es decir:
𝑄𝑄𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒 𝑒𝑒 𝑒𝑒 = −5 · 103
J
Mientras que el trabajo realizado por la máquina es el trabajo total del ciclo:
𝑊𝑊𝑡𝑡𝑡𝑡𝑡𝑡𝑎𝑎𝑎𝑎 = 773 J