Análisis gráfico de funciones racionales
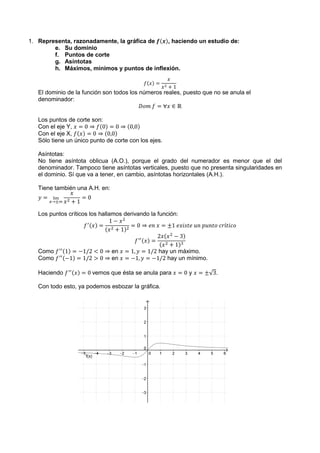
- 1. 1. Representa, razonadamente, la gráfica de 𝒇𝒇(𝒙𝒙), haciendo un estudio de: e. Su dominio f. Puntos de corte g. Asíntotas h. Máximos, mínimos y puntos de inflexión. 𝑓𝑓(𝑥𝑥) = 𝑥𝑥 𝑥𝑥2 + 1 El dominio de la función son todos los números reales, puesto que no se anula el denominador: 𝐷𝐷𝐷𝐷𝐷𝐷 𝑓𝑓 = ∀𝑥𝑥 ∈ ℝ Los puntos de corte son: Con el eje Y, 𝑥𝑥 = 0 ⇒ 𝑓𝑓(0) = 0 ⇒ (0,0) Con el eje X, 𝑓𝑓(𝑥𝑥) = 0 ⇒ (0,0) Sólo tiene un único punto de corte con los ejes. Asíntotas: No tiene asíntota oblicua (A.O.), porque el grado del numerador es menor que el del denominador. Tampoco tiene asíntotas verticales, puesto que no presenta singularidades en el dominio. Sí que va a tener, en cambio, asíntotas horizontales (A.H.). Tiene también una A.H. en: 𝑦𝑦 = lim 𝑥𝑥→±∞ 𝑥𝑥 𝑥𝑥2 + 1 = 0 Los puntos críticos los hallamos derivando la función: 𝑓𝑓′(𝑥𝑥) = 1 − 𝑥𝑥2 (𝑥𝑥2 + 1)2 = 0 ⇒ 𝑒𝑒𝑒𝑒 𝑥𝑥 = ±1 𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 𝑐𝑐𝑐𝑐í𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 𝑓𝑓′′(𝑥𝑥) = 2𝑥𝑥(𝑥𝑥2 − 3) (𝑥𝑥2 + 1)3 Como 𝑓𝑓′′(1) = −1/2 < 0 ⇒ en 𝑥𝑥 = 1, 𝑦𝑦 = 1/2 hay un máximo. Como 𝑓𝑓′′(−1) = 1/2 > 0 ⇒ en 𝑥𝑥 = −1, 𝑦𝑦 = −1/2 hay un mínimo. Haciendo 𝑓𝑓′′(𝑥𝑥) = 0 vemos que ésta se anula para 𝑥𝑥 = 0 y 𝑥𝑥 = ±√3. Con todo esto, ya podemos esbozar la gráfica.
- 2. 2. Representa, razonadamente, la gráfica de 𝒇𝒇(𝒙𝒙), haciendo un estudio de: a. Su dominio b. Puntos de corte c. Asíntotas d. Máximos, mínimos y puntos de inflexión. 𝑓𝑓(𝑥𝑥) = 𝑥𝑥2 − 2 𝑥𝑥 Lo primero de todo, vamos a operar para conseguir una función más fácil de manejar. 𝑓𝑓(𝑥𝑥) = 𝑥𝑥 − 2 𝑥𝑥 Lo que nos será útil más adelante cuando tengamos que derivar. El dominio de la función viene limitado por los puntos donde se anula el denominador, es decir: 𝐷𝐷𝐷𝐷𝐷𝐷 𝑓𝑓 = ℝ − {0} Puesto que tiene una indeterminación en 𝑥𝑥 = 0, sólo presenta puntos de corte con el eje X (𝑓𝑓(𝑥𝑥) = 0), donde 𝑥𝑥2 − 2 = 0 ⇒ 𝑥𝑥 = ±√2 Es decir, tiene dos puntos de corte con el eje X, en �−√2, 0� y en �√2, 0� No tiene asíntota horizontal (A.H.), porque el grado del numerador es una unidad mayor que el del denominador. Sí que va a tener, en cambio, asíntotas verticales (A.V.) y oblicuas (A.O.). Tiene una A.V. en 𝑥𝑥 = 0 y se da que: lim 𝑥𝑥→0+ 𝑥𝑥2 − 2 𝑥𝑥 = lim 𝑥𝑥→0+ 𝑥𝑥 − 2 𝑥𝑥 = −∞ lim 𝑥𝑥→0− 𝑥𝑥2 − 2 𝑥𝑥 = lim 𝑥𝑥→0− 𝑥𝑥 − 2 𝑥𝑥 = +∞ La pendiente de la asíntota oblicua la hallo mediante 𝑚𝑚 = lim 𝑥𝑥→+∞ 𝑓𝑓(𝑥𝑥) 𝑥𝑥 = lim 𝑥𝑥→+∞ 𝑥𝑥2 − 2 𝑥𝑥2 = 1 La ordenada en el origen se obtiene, a su vez, mediante 𝑛𝑛 = lim 𝑥𝑥→+∞ [𝑓𝑓(𝑥𝑥) − 𝑚𝑚𝑚𝑚] = lim 𝑥𝑥→+∞ � 𝑥𝑥2 − 2 𝑥𝑥 − 𝑥𝑥� = lim 𝑥𝑥→+∞ � 𝑥𝑥2 − 2 − 𝑥𝑥2 𝑥𝑥 � = lim 𝑥𝑥→+∞ −2 𝑥𝑥 = 0 Por lo tanto, 𝑓𝑓(𝑥𝑥) tendrá una asíntota oblicua en 𝑦𝑦 = 𝑥𝑥. Los puntos críticos los hallamos derivando la función: 𝑓𝑓′(𝑥𝑥) = 𝑑𝑑 𝑑𝑑𝑑𝑑 �𝑥𝑥 − 2 𝑥𝑥 � = 1 + 2 𝑥𝑥2 = 0 ⇒ 𝑥𝑥2 = −2 ≠ 0 ∀𝑥𝑥 ∈ ℝ ⇒ ∄𝑚𝑚á𝑥𝑥𝑥𝑥𝑥𝑥𝑥𝑥𝑥𝑥 𝑜𝑜 𝑚𝑚í𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛. La derivada segunda de 𝑓𝑓(𝑥𝑥), 𝑓𝑓′′(𝑥𝑥), nos dará los posibles puntos de inflexión: 𝑓𝑓′′(𝑥𝑥) = − 4 𝑥𝑥3 ≠ 0 ∀𝑥𝑥 ∈ ℝ Por lo que tampoco tiene puntos de inflexión. Ya con todo esto podemos hacernos una idea de cómo es la función y representarla.
- 3. 3. Representa, razonadamente, la gráfica de 𝒇𝒇(𝒙𝒙), haciendo un estudio de: a. Su dominio b. Puntos de corte c. Asíntotas d. Máximos, mínimos y puntos de inflexión. 𝑓𝑓(𝑥𝑥) = 𝑥𝑥2 𝑥𝑥2 − 1 El dominio de la función viene limitado por los puntos donde se anula el denominador: 𝐷𝐷𝐷𝐷𝐷𝐷 𝑓𝑓 = ℝ − {±1} Los puntos de corte son: Con el eje Y, 𝑥𝑥 = 0 ⇒ 𝑓𝑓(0) = 0 ⇒ (0,0) Con el eje X, 𝑓𝑓(𝑥𝑥) = 0 ⇒ (0,0) Sólo tiene un único punto de corte con los ejes. Asíntotas: No tiene asíntota oblicua (A.O.), porque el grado del numerador es igual al de denominador. Sí que va a tener, en cambio, asíntotas verticales (A.V.) y horizontales (A.H.). Tiene una A.V. en 𝑥𝑥 = 1 y otra en 𝑥𝑥 = −1 y se da que: lim 𝑥𝑥→1+ 𝑥𝑥2 𝑥𝑥2 − 1 = +∞ lim 𝑥𝑥→1− 𝑥𝑥2 𝑥𝑥2 − 1 = +∞ lim 𝑥𝑥→−1+ 𝑥𝑥2 𝑥𝑥2 − 1 = +∞ lim 𝑥𝑥→−1− 𝑥𝑥2 𝑥𝑥2 − 1 = +∞ Tiene también una A.H. en: 𝑦𝑦 = lim 𝑥𝑥→±∞ 𝑥𝑥2 𝑥𝑥2 − 1 = 1 Los puntos críticos los hallamos derivando la función: 𝑓𝑓′(𝑥𝑥) = 2𝑥𝑥(𝑥𝑥2 − 1) − 2𝑥𝑥 · 𝑥𝑥2 (𝑥𝑥2 − 1)2 = −2𝑥𝑥 (𝑥𝑥2 − 1)2 = 0 ⇒ 𝑒𝑒𝑒𝑒 𝑥𝑥 = 0 𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 𝑐𝑐𝑐𝑐í𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 𝑓𝑓′′(𝑥𝑥) = −2(𝑥𝑥2 − 1)2 + 8𝑥𝑥2(𝑥𝑥2 − 1) (𝑥𝑥2 − 1)4 = 6𝑥𝑥2 + 2 (𝑥𝑥2 − 1)3 Como 𝑓𝑓′′(0) = −2 < 0 ⇒ en 𝑥𝑥 = 0, 𝑦𝑦 = 0 hay un máximo en ese punto. También vemos que 𝑓𝑓′′(𝑥𝑥) ≠ 0 ∀𝑥𝑥 ∈ ℝ ⇒⇒ 𝑛𝑛𝑛𝑛 𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 𝑑𝑑𝑑𝑑 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖ó𝑛𝑛. Por lo tanto, con todos estos datos podemos dibujar la siguiente gráfica.
- 4. 4. Dada la siguiente función: 𝒇𝒇(𝒙𝒙) = 𝒙𝒙𝟐𝟐 + 𝟐𝟐𝟐𝟐 + 𝟏𝟏 𝒙𝒙 − 𝟏𝟏 a. Halla su dominio b. Estudia sus asíntotas. c. Represéntala cualitativamente. Como su dominio es: 𝐷𝐷𝐷𝐷𝐷𝐷 𝑓𝑓 = ∀𝑥𝑥ℝ − {1} es muy probable que presente una asíntota vertical en 𝑥𝑥 = 1, para ello debemos hacer los límites cuando 𝑥𝑥 → 1± . lim 𝑥𝑥→1+ 𝑥𝑥2 + 2𝑥𝑥 + 1 𝑥𝑥 − 1 = lim 𝑥𝑥→1+ (𝑥𝑥 + 1)2 𝑥𝑥 − 1 = +∞ lim 𝑥𝑥→1− 𝑥𝑥2 + 2𝑥𝑥 + 1 𝑥𝑥 − 1 = lim 𝑥𝑥→1− (𝑥𝑥 + 1)2 𝑥𝑥 − 1 = −∞ Es decir, presenta una discontinuidad inevitable en 𝑥𝑥 = 1 y, por tanto, tiene una asíntota vertical en dicho punto. Como el grado del numerador es mayor, en 1 unidad, que el del denominador, va a tener una asíntota oblicua del tipo 𝑦𝑦 = 𝑚𝑚𝑚𝑚 + 𝑛𝑛. La pendiente, 𝑚𝑚, la vamos a hallar por medio de: 𝑚𝑚 = lim 𝑥𝑥→+∞ 𝑓𝑓(𝑥𝑥) 𝑥𝑥 = lim 𝑥𝑥→+∞ 𝑥𝑥2 + 2𝑥𝑥 + 1 𝑥𝑥2 − 𝑥𝑥 = lim 𝑥𝑥→+∞ 𝑥𝑥2 𝑥𝑥2 = 1 La ordenada en el origen, en cambio, será: 𝑛𝑛 = lim 𝑥𝑥→+∞ � 𝑥𝑥2 + 2𝑥𝑥 + 1 𝑥𝑥 − 1 − 𝑥𝑥� = lim 𝑥𝑥→+∞ � 𝑥𝑥2 + 2𝑥𝑥 + 1 − 𝑥𝑥2 + 𝑥𝑥 𝑥𝑥 − 1 � = lim 𝑥𝑥→+∞ � 3𝑥𝑥 + 1 𝑥𝑥 − 1 � = 3 Por lo tanto, la asíntota vertical corresponderá a la recta: 𝑦𝑦 = 𝑥𝑥 + 2 Con estos datos, podemos dibujar cualitativamente la recta tal y como se muestra a continuación.
- 5. 5. Dada la función: 𝒇𝒇(𝒙𝒙) = 𝒆𝒆−𝒙𝒙𝟐𝟐 Calcula: a. Asíntotas. b. Máximos, mínimos y puntos de inflexión. c. Dibújala. Como su dominio son todos los números reales, no va a tener asíntota vertical; y como no es un cociente, tampoco va a tener asíntota oblicua. Sin embargo, sí va a tener asíntota horizontal: lim 𝑥𝑥→± ∞ 𝑒𝑒−𝑥𝑥2 = 0 Va a tener una asíntota horizontal en 𝑦𝑦 = 0. Para hallar los máximos, mínimos y puntos de inflexión, derivamos e igualamos a cero: 𝑓𝑓′(𝑥𝑥) = −2𝑥𝑥𝑒𝑒−𝑥𝑥2 = 0 ⇒ 𝑥𝑥 = 0 Para discriminar si en 𝑥𝑥 = 0 tenemos un máximo o un mínimo, tenemos que hacer la segunda derivada. 𝑓𝑓′′(𝑥𝑥). 𝑓𝑓′′(𝑥𝑥) = −2𝑒𝑒−𝑥𝑥2 + 4𝑥𝑥2 𝑒𝑒−𝑥𝑥2 ⇒ 𝑓𝑓′′(0) = −2 < 0 Por lo tanto, en 𝑥𝑥 = 0 e 𝑦𝑦 = 𝑓𝑓(0) = 1, tenemos un máximo. Los puntos de inflexión los hallamos mediante 𝑓𝑓′′(𝑥𝑥) = 0. 𝑓𝑓′′(𝑥𝑥) = −2𝑒𝑒−𝑥𝑥2 + 4𝑥𝑥2 𝑒𝑒−𝑥𝑥2 = 𝑒𝑒−𝑥𝑥2 (−2 + 4𝑥𝑥2) = 0 ⇒ −2 + 4𝑥𝑥2 = 0 ⇒ ⇒ 𝑥𝑥 = ± 1 √2 = ± √2 2 Para comprobarlo, tenemos que hacer 𝑓𝑓′′′(𝑥𝑥) 𝑓𝑓′′′(𝑥𝑥) = −2𝑥𝑥𝑒𝑒−𝑥𝑥2 (−2 + 4𝑥𝑥2) + 8𝑥𝑥𝑒𝑒−𝑥𝑥2 = 𝑒𝑒−𝑥𝑥2 (4𝑥𝑥2 + 8𝑥𝑥 − 2) Si hacemos 𝑓𝑓’’’ �± √2 2 � ≠ 0, por lo que sí son puntos de inflexión. Por lo tanto, la gráfica pedida será:
- 6. 6. Representa, razonadamente, la gráfica de 𝒇𝒇(𝒙𝒙), haciendo un estudio de: a. Su dominio. b. Puntos de corte. c. Asíntotas. d. Máximos, mínimos y puntos de inflexión. 𝒇𝒇(𝒙𝒙) = 𝒙𝒙𝟐𝟐 + 𝟖𝟖 𝒙𝒙𝟐𝟐 − 𝟒𝟒 El dominio de la función viene limitado por los puntos donde se anula el denominador: 𝐷𝐷𝐷𝐷𝐷𝐷 𝑓𝑓 = ℝ − {±2} Los puntos de corte son: Con el eje Y, 𝑥𝑥 = 0 ⇒ 𝑓𝑓(0) = −2 ⇒ (0, −2) Con el eje X no corta, puesto que, 𝑓𝑓(𝑥𝑥) ≠ 0 ∀𝑥𝑥 ∈ ℝ Sólo tiene un único punto de corte con los ejes. Asíntotas: No tiene asíntota oblicua (A.O.), porque el grado del numerador es igual al de denominador. Sí que va a tener, en cambio, asíntotas verticales (A.V.) y horizontales (A.H.). Tiene una A.V. en 𝑥𝑥 = 2 y otra en 𝑥𝑥 = −2 y se da que: lim 𝑥𝑥→2+ 𝑥𝑥2 + 8 𝑥𝑥2 − 4 = +∞ lim 𝑥𝑥→2− 𝑥𝑥2 + 8 𝑥𝑥2 − 4 = −∞ lim 𝑥𝑥→−2+ 𝑥𝑥2 + 8 𝑥𝑥2 − 4 = −∞ lim 𝑥𝑥→−2− 𝑥𝑥2 + 8 𝑥𝑥2 − 4 = +∞ Tiene también una A.H. en: 𝑦𝑦 = lim 𝑥𝑥→±∞ 𝑥𝑥2 + 8 𝑥𝑥2 − 4 = 1 Los puntos críticos los hallamos derivando la función: 𝑓𝑓′(𝑥𝑥) = 2𝑥𝑥(𝑥𝑥2 − 4) − 2𝑥𝑥 · (𝑥𝑥2 + 8) (𝑥𝑥2 − 4)2 = −24𝑥𝑥 (𝑥𝑥2 − 4)2 = 0 ⇒ 𝑒𝑒𝑒𝑒 𝑥𝑥 = 0 𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 𝑐𝑐𝑐𝑐í𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 𝑓𝑓′′(𝑥𝑥) = −24(𝑥𝑥2 − 4)2 + 96𝑥𝑥2(𝑥𝑥2 − 4) (𝑥𝑥2 − 4)4 = 24(3𝑥𝑥2 + 4) (𝑥𝑥2 − 4)3 Como 𝑓𝑓′′(0) = −3/2 < 0 ⇒ en 𝑥𝑥 = 0, 𝑦𝑦 = −2 hay un máximo en ese punto. También vemos que 𝑓𝑓′′(𝑥𝑥) ≠ 0 ∀𝑥𝑥 ∈ ℝ ⇒ 𝑛𝑛𝑛𝑛 𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 𝑑𝑑𝑑𝑑 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖ó𝑛𝑛. Por lo tanto, con todos estos datos podemos dibujar la siguiente gráfica.
