resumen de temas como potencias, factorización, polinomios, identidades trigonometricas, limites, etc

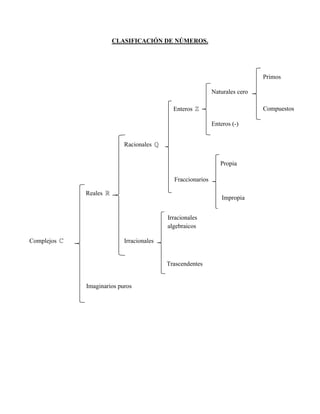
1. CLASIFICACIÓN DE NÚMEROS.
Complejos
Reales
Imaginarios puros
Irracionales
Racionales
Enteros
Fraccionarios
Trascendentes
Irracionales algebraicos
Enteros (-)
Naturales cero
Impropia
Propia
Compuestos
Primos

2. NÚMEROS COMPLEJOS.
z  a bi en 0 q a y b se llama número complejo.
a  Parte real del número complejo z
b  Parte imaginaria del número complejo z
Si a  0 bi se llama imaginario puro
Si b  0 a es real
1 1 1 2 2 2 z  x iy ; z  x iy
1 2 z  z = 1 2 1 2 (x  x )  i(y  y )
1 2 1 2 1 2 1 2 1 2 z  z  (x x  y y )  (x y  y x )i
1 1 1 1 1 2 2 1 2 1 2 1 2 1 2
2 2 2 2
2 2 2 2 2 2 2 2 2 2 2
( ) ( )
( ) ( )
z x iy x iy x iy x x y y iy x x y
z x iy x iy x iy x y x y
    
   
    
0
1
2
3
4
1
1
1
1
1
i
i i
i
i i
i

  
 
    

En general  n  :
4 3 1 ni i    
4 2 1 n i   
4 1 1 ni i      
4 1 n i 
Conjugado de un número complejo a bi es a bi .
Opuesto de un número complejo a bi es a bi .

3. 1 z 1i 2 z  2i
1) 1 2 z  z
2) 2 1 z  z
3) 1 2 z  z
4) 2
1
z
z
5) 1
2
z
z
6) 2(3i)4(5i) 7(4i)
7) 2 (32i)
8)
2 4
4 2
i
i


9)
2 5
(1 )
3 2
i
i
i



10) (32i)(42i)
Tarea: Dados 1 z = 3 6i ; 2 z  52i ; 3
4
3
z  ; 4 z  5i
Calcular:
a) 1 2 3 (z  z )z
b) 1 4 3 4 z z  z z
c) 1 4 2 z  z  5z
d) 1
1 3 z z 
e) 1
2 z
f) 1 2 z z
g)
1
1 2 (z z )


h) 2
1 3 z z
i) 2
1
z
z
j) 1
3 4 2
z
z  z
Reales Fracciones
Suma =
1 1 2
1
2 2 2
  
Resta =
1 1 0
0
2 2 2
  
Multiplicación =
1 1 1
2 2 4
 
División =
1 1 2
1
2 2 2
  

4. POTENCIAS.
( factores ) n a  aaa n a
5 y  y y y y y
5
4
3
3 4 7
2 32
( 3) 81
1 1
2 8
x x x

 
 
    
 
 
Teorema 1: Si n y m son enteros positivos y a :
n m n m a a a   
3 2 5
3 7 10
(2) (2) 2 32
y y y
 
 
Ejercicios: Obtener los siguientes productos.
4 3 5 2 9 5
5 4 2 9
(4 )( 5 ) 20
(4 )(5 ) 20 n n n
x y x y x y
nx nx n x
  

Teorema 2: Si n y m son enteros positivos y a :
( ) n m n m a a 
3 2 6
2 5 10
(2 ) 2 64
(x ) x
 

Ejercicios: 2 2 2 ( ) ;( ) ;( ) n n n n x x
Teorema 3: Si n es un entero positivo y a y b :
( )n n n ab  a b
2
3 3 3
4 5 10 20
3 4 12
(2 5) 2 5
( )
(30 ) 810
x y x y
  



5. Ejercicios: Evaluar cada uno de los siguientes productos:
a) 3 4 2 5 4 2 5 10 6 (5r s t )(6s t )(r s)  30r s t
b) 3 2 3 2 3 4 4 17 18 19 (2x y z) (x y z ) 81 y z
4 (1)
Teorema 4: Si n y m son enteros positivos y a  0 :
n
m
a
a

6 3 5
4
2 7 4 5
1
1
x x x
x
x x x x
  
Obtener los siguientes cocientes:
5 2 2 6
3
3 8 6 3
8 4 6
2
2 3
n
n
n
a b a nx
x
a b b nx
 
Teorema 5: Si n es un entero positivo y a y b ;b  0
n n
n
a a
b b
 
  
 
5 3 5 4 2 4 2 3 12 6
5 3 3 3 9
2 2 32 ( )
3 3 243 ( )
x z x z x z
y y y
   
       
   
Exponente cero y exponente entero negativo.
Si n es un entero positivo y a es un número real  0
0
1
1 n
n
a
a
a



3 2 1 3 2 1
3 2
1 72
(2 3 ) 72 (2 3 )
(2 3 ) 17
     
      

Si n>m n m a 
Si n<m
1
m n a 
Si n=m 1

6. Escriba las siguientes expresiones como fracción simple usando únicamente
exponentes positivos:
2
3 4 5 18 2
6 2 4 12
x y z x z
x y z y

 
 
 
  
 
3 2 4 2 5 7 3 8
3 2 4
4 4 4 4
( 3 )( 2 ) 6
2
3 3
x yz x y z x y z
x y z
x yz x yz
 
  
 
2 3 4 2 2
2 2
4 2
(20 )(2 ) 10
( 4 )(3 ) 3
r s t r s t
r t
rst rs t
 


7. RADICALES.
= radicando
n= índice del radical
aa  a
 
2 ;
n
n
a b b a
a a
 

Ley de los radicales:
i) n n n ab  a b
ii)
n
n
n
a a
b b

iii)
m n mn a  a
iv)  m
m n n n m a  a  a
v)
1 1 ( ) ( ) m n n m m n a  a  a
Suma y resta
n=n
a=a
Producto y división
n=n
Racionalización del denominador.
Productos notables:
i) 2 2 (x  y)(x  y)  x  y
ii) 2 (ax b)(cx d)  acx (ad bc)x bd
iii) 2 2 2 (x  y)  x  2xy  y
iv) 2 2 2 (x  y)  x 2xy  y
v) 3 3 2 2 3 (x  y)  x 3x y 3xy  y
vi) 3 3 2 2 3 (x  y)  x 3x y 3xy  y
Factorización:
2 2
3 3 2 2
3 3 2 2
( )( ) Diferencia de dos cuadrados
( )( ) Diferencia de dos cubos
( )( ) Suma de dos cubos
a b a b a b
a b a b a ab b
a b a b a ab b
   
    
    

8. Factorización de polinomios:
2 px  qx r; Donde p, q y r son enteros.
(ax b)(cx d); Donde a, b, c y d son enteros.
ac  p; bd  r; ad bc  q
Ejercicios:
50  5 2 ; 50  252  5 2
3 6 3 64  2 ; 64  8  2
3 3 3 3 3 3 320  645  4 5  4 5
2 6 1 3 2 3 2 3 2 2 (r s )  r s  r s
3 6 3 4  16  2 4
40  90  5 10
4 6 12 4 2 6 3 12 6 4  8  64  2  2  2  2  2  2  2
3 3 3
3 3 3
1 5 5 25
2 5 5 5 2 5 10
  
 
 
 
4
4 5 4
5 4 16 5 5 16 5 15 3 5 5
5 4 5 4 5 4 5 4 4 4 4
5 4
1 1 x x x x x x x x x
x x x x x x x x x
  
        
 
 
 
 2
2
2 3 1 2 3 1
3 1 3 1 3 1
 
 
  
7 3 7 3
7 4 7 4 7 3 7 7
1 1x x
x x x x
 


9. Productos notables:
a)    2 2 4 2r  5 2r  5  4r 5
b)  2
c 1 c  c  2 1 c
c)  3 3 2 2 3 2a 5b  8a  60a b 150ab 125b
Factorización:
a) 2 2 2 2 (25r 49s )  (5r) (7s)  (5r 7s)(5r 7s)
b) 4 4 2 2 2 2 2 2 2 2 2 2 81x  y  (9x ) (y )  (9x  y )(9x  y )  (9x  y )(3x  y)(3x  y)
c) 3 3 3 3 2 2 2 2 a  64b  a  (4b)  (a  4b) a  a(4b)  (4b)   (a  4b)(a  4ab 16b )
d)
2
6 9 2 3 3 3 2 3 2 2 2 3 3 2 3 4 2 3 6 8x  27y  (2x ) (3y )  (2x 3y ) (2x )  (2x )3y )  (3y )  (2x 3y )(4x  6x y 9y )

10. POLINOMIOS.
1 1 0
1 1 0 ( ) ... n n
n n P x a x a x a x a x a 
       
Monomio = un término 3x
Binomio = dos términos x2  2y
Trinomio = tres términos a  abc
Polinomio = uno o más términos 3 2 x  2x 3x 7
Grado mayor, exponente en que se encuentra la variable x.
2 2 2 2 6x  x 73x 4x  (63)x (14)x 7  9x 3x 7
2 2 2 2 2 2 2 7a b3a b8ab 5ab 6ab  4a b3ab
Suma:
3 2 3 2 3 2 (4y 7y 3y 8) (6y 2y 4) 10y 5y 3y 4
Resta:
3 2 3 2 3 2 (2a a 4a 3)(4a 8a 2a 6)  2a 9a  2a9
Multiplicación:
2
2 2 9 3 2
2 2 3 2 2 3
(2 7)(3 4) 6 13 28
(3 2 1) (3 4 ) 12 11 3 5 3
(5 4 ) (2 3 ) 10 17 11 12
x x x x
x x x x x x x x x
x xy y x x y x x y xy y
    
         
      
División:
5 4 2 2 3 4 5 4 2 2 3 4
4 2 3
2 2 2
30 18 30 18
5 3
6 6 6
x y z x y z x y z x y z
x y z xyz
xy z xy z xy z
 
    
  

11. 2 2 3 11 18 6
5
z z z
z
  

3 3 x y
x y


3 2 3
2 2
x 0x 0x y
x xy y
  
 
6 21 21
6 5 6
3 3 18
( ) 1 ( ) 1 9
9 3 ( ) 3
4 2 ( ) 2 2
xy xy xy
xy xy xy xy xy xy xy xy
xy x y xy
         
2 3x 4 6x 13x 28
2x  7
Divisor
Cociente
Dividendo
2 6x 8x
21x  28 Residuo

12. Si la expresión analítica de la función es un polinomio el dominio son todos los números
reales:
Ejemplo: 4 2 f (x)  x  4x 1
Dom f (x) =
Cont f (x) = (,5]
Si la expresión analítica de la función es un cociente, el dominio son todos los reales
excepto los que anulan el denominador:
Ejemplo:
2
( )
1
f x
x


Dom f (x) = - {-1}
Cont f (x) = (,0)(0,)
Si la expresión analítica de la función es una raíz cuadrada el dominio está formado por los
números reales para los que:
f (x)  x 3
Dom f (x) = [3,)
Cont f (x) = [0,)
1
( )
2
f x
x


Dom f (x) = (2,)
Cont f (x) = (0,)
f (x)  x 3
Dom f (x) = { }
Cont f (x) = (,)
2
3
x
x


Dom -{3}
Cont (,1)(1,)

13. FUNCIONES Y SUS GRÁFICAS.
Par ordenado = 2 números reales
(a,b) (c,d)
a c
b d



Plano cartesiano a  abscisa o coordenada x
b  ordenada o coordenada y
Plano xy:
I = x (+) , y (+)
II = x (-) , y(+)
III = x (-) , y(-)
IV = x (+) , y(-)
P = ( a,b )
1
2
( 2, 3)
(4, 2)
P
P
  
 
1 2
1 1 1 2 2 2
2 2
1 2 2 1 2 1
1 1 1 2 2 2
1 2 1 2
( , )
( , ) ( , )
( , ) ( ) ( )
( , ) ( , )
,
2 2
d P P
P x y P x y
d P P x x y y
P x y P x y
x x y y
   
   
 
 
Hallar el punto medio M del segmento de recta de 1 P (-2,3) a 2 P (4,-2). Representar los
puntos 1 P , 2 P y M y verificar que 1 d(P,M)  9  25 4 , 2 d(P ,M)  9  25 4 .
II
III IV
I
y
x

14. Describa en un plano cartesiano el conjunto de todos los puntos P(x,y) tales que:
a) x  3
b) y  1
c) x  0
d) xy> 0
e) y < 0
Gráficas:
“La frase trazar la gráfica de W” significa, ilustrar geométricamente en un plano
coordenado las características de la gráfica.
W {(x, y) : y  2x 1}
X 0 1 2 3
Y -1 1 3 5
2 y  x = Parábola
X -3 -2 -1 0 1 2 3
Y 9 4 1 0 1 4 9
Eje Y = Eje de la parábola.
(0,0) = Vértice de la parábola.
2 y  ax a  0 Parábola con vértice (0,0)
Lado derecho es simétrico con el lado izquierdo.
Pruebas de simetría:
i) La gráfica de una ecuación es simétrica con respecto al eje Y si la sustitución de
X por –X da una ecuación equivalente.
ii) Lá gráfica de una ecuación es simétrica con respecto al eje X si la sustitución de
Y por –Y da una ecuación equivalente.
iii) La gráfica de una ecuación es simétrica con respecto al origen si la sustitución
simultánea de X por –X y de Y por –Y da una ecuación equivalente.
2 3
3
4
4
y x y x
y x
 
  

15. Si C(h,k) es un punto del plano coordenado radio r > 0
P(x,y) sobre la circunferencia d(C,P) = r
2 2
2 2 2
2 2 2
( ) ( ) ecuación de la circunferencia
( ) ( )
0 y 0
centro en el orígen
x h y k r
r x h y k
h k
r x y
    
   
 
  
Obtener la ecuación de la circunferencia con centro C(-2,3) y que pasa por el punto D(4,5).
 2 2
2 2
2 2
2 2
(4 ( 2) (5 3) 40
2 y 3
( 2) ( 3) 40
4 4 6 9 40
4 6 27 0
h k
x y
x x y y
x y x y
    
  
   
     
    
Hallar el centro y radio de la circunferencia cuya ecuación está dada por
x2  y2 4x 6y 3  0 .
2 2
2 2
2 2
2 2
4 6 3 0
( 4 ) ( 6 ) 3
( 4 4) ( 6 9) 3 4 9
( 2) ( 3) 16
(2, 3) 16
x y x y
x x y y
x x y y
x y
C r
    
   
       
   
 
Graficar:
9.- y  3x 1
15.- 2 y  2x
20.- 2 3y  x  0
23.- 3 y  x 2
33.- 2 2 x  y 16
35.- 2 2 9x 9y 1
37.- 2 2 (x 2) (y 4) 1
39.- 2 2 x (y 3)  9
41.- Centro C(3,-2) r = 4
43.- Centro C(1/2, -3/2)
42.- Centro C(-5,2) r = 5
51.- 2 2 x  y 2x 10y 10  0
52.- 2 2 x  y 8x  4y 15  0
53.- 2 2 x  y 6y 5  0

16. Funciones: Una función puede considerarse como la correspondencia entre un conjunto X
de números reales X, y otro conjunto Y de números reales Y, donde el número Y es único
para un valor dado de X.
2
2
2 2
( ) 2
2 5
( , )
[5, )
16
f x x
y x
x y
 
 
 

 
X -4 -3/2 -1 0 1 3/2 4
Y 16 9/4 1 0 1 9/4 16
2•
3•
1•
5•
7•
0•
1•
2•
3•
4•
5•
6•
Dominio
X
Contradominio
Y

17. [0,16]
[-4,4]
Dominio (,3][3,)
Contradominio [0,)
x = variable independiente
y = variable dependiente
4
( )
1
4 0 y 1 0
4 1
[ 4,1) (1, )
x
y x
x
x x
x x



   
  
  
a) El dominio de g
b) g(5), g(2), g(a),3/ 4, 2 3, 4 9 1 a
Una función f con dominio D es:
i) Par si f (x) = f (x) para todo x en D
4•
-4•
-3/2•
3/2•
-1•
1•
0•
16•
9/4•
-1•
0•

18. ii) Impar si f (x) = - f (x) para todo x en D
a) Si f (x) = 4 2 3x 2x 5 ; función par.
b) Si 5 3 g(x)  2x 7x 4x ; función impar.
Ejemplo:
La función h se define como h {(x, y) : y | x |}. Trazar la gráfica de h y determinar el
dominio y el contradominio.
D = (,)
C = [0,)
Sea F la función que corresponde al conjunto de todos los pares ordenados tales que
2
{3 2 si 1
{1 2( 1) si 1
y x x
y x x
  
  
Trazar la gráfica de F y determinar el dominio y contradominio.
D = (,)
C = (,)

19. Si f (x) = 2 9  x trazar la gráfica de f y encontrar el D y C.
2 ( ) 3
( , )
[ 3, )
f x x
D
C
 
 
 
Decreciente.
(,0)
Creciente.
(0,)
Dominio
[3,3]
Contradominio
[0,3]

20. 1 1 0
1 1 0 ( ) ... n n
n n P x a x a x a x a x a 
       
f (x)  x 1 Creciente.
Dominio y contradominio
[1,) [0,)
2 9
3
x
y
x



; x 3 2 x  0x 9
x 3
2 x 3x
3x 9
3x 9
0
2 y  x
2 y  (x 4)
2 y  (x  2)

21. Traslaciones verticales.
( ) abajo
( ) = arriba
y f x C C
y f x C C
  
 
( ) derecha
( ) = izquierda
y f x C C
y f x C C
  
 
2
1 angosta
1 ancha
x n
n
n


Swokowski = 176
Leithold = 255
n a
n
a) Positiva Par Desciende desde la izquierda, asciende hacia la derecha
b) Positiva Impar Asciende desde la izquierda, asciende hacia la derecha.
c) Negativa Par Asciende desde la izquierda, desciende hacia la derecha.
d) Negativa Impar
Desciende desde la izquierda, desciende hacia la
derecha.
y  x2
2 y  x 2
2 y  x  4

22. 2 y k  a(x h) Ecuación de la parábola (eje vertical).
2
3
( ) 3 24 50
( ) 2 6 4
f x x x
f x x x
  
  
(a)
(b)
(c) (d)
2 y  ax
(h,0) 2 y  a(x h)

23. 3 2 P(x)  x 6x 9x 4
X -2 -1 0 1 2 3 4 5
P(x) -54 -20 -4 0 -2 -4 0 16
(h,k)
2 y  a(x h)  k

24. 4 3 2 P(x)  3x 4x 12x 12
X -2 -1 0 1 2 3
F(x) 44 7 12 -1 -20 -39

25. FUNCIONES RACIONALES.
Es el cociente de dos funciones polinomiales *
( )
( )
( )
P x
f x
Q x

Si P y Q son funciones polinomiales y f es la función definida por * entonces f es una
función racional, El dominio de f es el conjunto de todos los números reales excepto los
ceros de Q.
2
( )
3
x
f x
x



X 4
7/2
(3.5)
10/3(3.3) 13/4(2.25) 31/10 301/10 30001/1000(3.001)
F(x) 6 11 16 21 51 501 5001
f x 3   
X 2 5/2(2.5) 8/3(2.6) 11/4(2.75) 29/10 299/100 2999/1000
F(x) -4 -9 -14 -19 -49 -499 -4999
f x 3   
Asíntota
vertical.
i) iv)
i) iiii)

26. Asíntota vertical: Se dice que la recta x  a es una asíntota vertical de la gráfica de la
función f cuando por lo menos uno de los siguientes enunciados es cierto:
i) f (x) a medida que x a


ii) f (x) a medida que x a 
iii) f (x) a medida que x a 
iv) f (x) a medida que x a 
Asíntota horizontal: Se dice que la recta y  b es una asíntota horizontal de la gráfica de
la función f cuando por lo menos uno de los siguientes enunciados es cierto:
i) f (x) b  a medida que x  
ii) f (x) b  a medida que x  
iii) f (x) b  a medida que x  
iv) f (x) b  a medida que x  
i) iv) ii)
iii)

27. La gráfica de una función racional de la forma:
1
1 1 0
1
1 1 0
...
...
n n
n n
m m
m m
a x a x a x a
b x b x b x b




   
   
Tiene:
i) Al eje x como asíntota horizontal cuando n<m
ii) A la recta n
m
a
y
b
 como asíntota horizontal cuando n=m
iii) Ninguna asíntota horizontal cuando n>m
Tarea:
2
2
2 3 3
( ) ( )
1 2 32
x x
f x f x
x x

 
 
2
2
4 4
( ) ó ( )
25 ( 5)( 5)
x x
f x f x
x x x
 
  
FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.
Tarea:
2
3
3 2
4 2
5 3
( ) 2
( ) 2
( ) 3 3
( ) 5 4
( ) 4
f x x
f x x
f x x x
f x x x
f x x x

 
  
  
 

28. Teorema 1: Si n y m son números racionales entonces:
i) Si a > 1, n < m implica que n m a  a
ii) Si 0 < a < 1, n < m implica que n m a  a
a = 4, n = 2, m = 3 2 3 4  4 a = 1/3     2 3
1 1
3 3

Teorema 2: Si a y b son números positivos cualesquiera, y n y m son números positivos
cualesquiera entonces:
i) n m n m a a a  
ii)
m
m n
n
a
a
a
 
iii) ( ) m n mn a  a
iv) ( )n n n ab  a b
v)
n n
n
a a
b b
 
  
 
Ejercicios:
3 12 3 3 2 2  2   20
5 10 7  7
*El número e  2.7182818
Función exponencial de base a
Si a > 0 y a  1, entonces la función exponencial de base a es la función f definida:
( ) x f x  a
Donde el dominio de f es el conjunto de números reales y el contradominio es el conjunto
de números positivos.
 Representar gráficamente f siendo ( ) 2x f x 
X -3 -2 -1 0 1 2 3 4
F(x) 1/6 1/4 1/2 1 2 4 8 16

29. Crecimiento exponencial. Decrecimiento exponencial.
Trazar la gráfica de f si
2
( ) 2 x f x  
X -2 -1 0 1 2
F(x) 1/16 1/2 1 1/2 1/16
3 ( ) 2
( ) 3 3
x
x x
f x
f x



 
y  ax ;a 1
0 1
x y a
a

 

30. Función exponencial natural *
La función exponencial natural es la función f definida por f (x)  ex , donde el dominio
es el conjunto de los números reales y su contradominio es el conjunto de los números (+).
X 0 0.5 1 1.5 2 2.5 -0.5 -1 -2
x e 1 1.6 2.7 4.5 7.4 12.2 0.6 0.4 0.1
.
Encontrar las raíces de f si
2 2 2 ( ) ( 2 ) 2 x x f x x e xe     
2 2 2
2
2
2
( ) 2 2
( ) 2 (1 )
1 0 2xe 0
1 2xe 0
x x
x
x
x
f x xe x e
f x xe x
x
x
 



 
 
  
 
( ) ( 1) x x x f x  xe e  e x 
-1 y 0
3 4 2 4
2 4
( ) (4 ) 3
( ) (4 3)
x x
x
f x x e x e
f x x e x
 
 
x  0
4 3
3
4
x
x

 

31. 9.-
2
3 4 2 4
2 2 2 2 2
( )
( ) 2
( ) (4 ) 3
( ) (2 ) 2 2 éste no
x x
x x
x x
x x x x
f x xe e
f x x e xe
f x x e x e
f x x e xe e xe
 
 
  
 
   
13.- 2
( )( ) ( )( )
( )
x x x x x x x x
x x
e e e e e e e e
e e
   

    

La función logarítmica de base a es la inversa a la función exponencial de base a.
log si y sólo si x
x  a y y  a
3
2
1/2
2
5
2 8
5 1/ 25
1/16 1/ 4
3 log 8
2 log 1/ 25
1/ 2 log1/16 1/ 4





 

Teorema:
i)
loga x a  x para toda x > 0
ii) log 1 a a 
iii) log 1 0 a 
Dominio = Reales positivos.
Contradominio = Reales.
Resolver las siguientes ecuaciones:
a) 6 log 2
36
x
x


b) 27 log 2 / 3
9
x
x


c)
log 81 2
1/ 9
x
x
 

4 log (5 ) 3
59
x
x
 


32. Leyes de los logaritmos:
i) log ( ) log log a a a uw  u  w
ii) log log log a a a
u
u w
w
 
   
 
iii) log ( ) log para todo número real c. c
a a u  c u
Si u=4, w=8, a=2 y c=3.
log ( ) log log a a a uw  u  w
log log log a a a
u
u w
w
 
   
 
log ( ) log c
a a u  c u
Expresar cada uno de los siguientes casos en términos de logaritmos de x, y, z en los que
estas variables representen números (+).
a) 2 3 4 loga x y z
b) 2 loga
x
yz
c)
2
5
3 loga
xy
z
* 2 3 4 log log log a a a x  y  z
a) 2log 3log 4log a a a x  y  z
b) log log 2log a a a x  y  z
c)
1 2 3
log log log
5 5 5 a a a x  y  z
Escribir cada una de las siguientes expresiones como un solo logaritmo con coeficiente
1.
a)
2
3 log 2log 3log log a a a a
xy
x y z
z
  
b)  
2
3
1 4 log 4 log 3 2log log log
3 3 a a a a a
x
x y
y
   
La función logarítmica natural es la inversa de la función exponencial natural.

33. ln
ln si y sólo si
ln 1
y ln
x
x x
x y y e
e
e x e x
 

 
i) ln(uw)  lnu lnw
ii) ln ln ln
u
u w
w
 
   
 
iii) ln ln c u  c u
Ecuaciones exponenciales y logarítmicas.
Obtener el conjunto de soluciones de la ecuación:
(1)
3 21
log3 log 21
log3 log 21
log 21
2.77
log3
x
x
x
x



 
Resolver la ecuación:
(2)
2 1 5 6 2
{ 3.64}
x x
x
  
 
(3)
 
log(5 1) log( 3) 2
299
95
x x
x
   

(4)
3 1 5 0.08
{ 0.1897}
x
x
 
 
(5)
1 7 3
{1.296}
x x
x
 

(6)

34. 1 7 3
1.296
x x
x
 

(7)
10
2
log ( 3) 2
3 10
x
x
 
 
(8)
2 2
2
3
log ( 4) log ( 3) 3
log 3
2 4
x x
a
b
a
b
   

 
(9)
3 3
2 3
2
log log (2 3) 3
log( ) 3
2 3 3
2 3 27 0
( 3)(2 9) 0
x x
ab
x x
x x
x x
  

 
  
  
2
2
3 3 4
1
3 4
3
3 1 4(3 )
(3 ) 4(3 ) 1 0
3
2 5
x x
x
x x
x x
x
x u
u
  
 
 
  

 
3 2 5
log3 log(2 5)
log3 log(2 5)
1.314
conjunto de soluciones
x
x
x
x
 
 
 

e3x  21 y  ln x
3
21
3 ln 21
y x e
x y
x
x




4 4
3 3
10 10 10 10
2 2 2
Tarea:
log (2 3) 2log 2
*log (2 3) log ( 3) 4
log log ( 200) log 4 5 log 5
*log ( 2) 3 log 3 log
x x
x x
x x
x x
  
   
    
   

35. CONVERSIONES DE UNIDADES ANGULARES
En geometría un ángulo se determina por dos rayas o semirrecta 1 l y 2 l con el mismo punto
inicial O. Si A y B son puntos en 1 l y 2 l respectivamente entonces nos podemos referir al
ángulo AOB.
Ángulo positivo. Ángulo negativo.
Si el lado terminal coincide con un eje coordenado, entonces al ángulo se le llama ángulo
cuadrantal.
grado
1
1°=
360
90 ángulo recto
0 90 ángulo agudo
90 180 ángulo obtuso


 
 
    
    
*Éstos ángulos siempre tienen
medidas de grados que difieren
en un múltiplo de 360°.
60°+360°=420°+720°=780°
2 ángulos agudos son complementarios si suman 90°.
2 ángulos positivos son suplementarios si suman 180°.
O
A
B
Lado inicial

2 l
1 l

1 l
2 l

36. Se llaman ángulos coterminales a aquellos que tienen los mismos lados inicial y teminal.
1 grado dividirlo en 60 partes iguales minuto (‘) y cada minuto en 60 partes iguales
llamadas segundo (‘’)
1 1
1' 1° y 1'' 1°
60 3600
 
  7356'18''
Hallar el ángulo complementario de  si:
 = 25°43’37’’  =73.26°
Un ángulo tiene una medida de 1 radián, si al colocar su vértice en el centro de un círculo,
la longitud del arco interceptado en la circunferencia es igual al radio.
P
A
360 2 radianes
180° = radianes
1° = radianes
180
180
1 radián =

  


 
 
  
1°  0.0174533 radianes y 1 radián = 57.29578° .
a)
5 5
150 , 225 en radianes ,
6 4
 
 
    

r
r

37. b)
7
, en grados 315 ,60
4 3
 
 
    
Radianes 0 6

4

3

2
 2
3
 3
4
 5
6
 
Grados 0° 30° 45° 60° 90° 120° 135° 150° 180°
7
6
 5
4
 4
3
 3
2
 5
3
 7
4
 11
6
 2
210° 225° 240° 270° 300° 315° 330° 360°
Teorema de Pitágoras, ley de senos y cosenos, triángulos semejantes.
En todo triángulo-rectángulo el cuadrado de la hipotenusa, es igual a la suma de los
cuadrados de los catetos.
c
a
b
cos
tan
a
sen
c
b
c
a
b






2 2 2
2 2
2 2
c a b
a c b
b c a
 
 
 

38. Triángulos oblicuos.
Si en un triángulo ABC, las medidas de los lados opuestos a los ángulos A, B y C son
respectivamente a, b, c entonces:
a b x
sen sen sen
 
A
b
B C
CASO I:
62.5 112 42
/ ,
a
B b c
      
CASO II:
C=25 =35° =68°
, ,
* 31.5 b=51.8 33
, ,
ABC
c a b
a
c
 

 
  
Ley de los cosenos.
En cualquier triángulo ABC, el cuadrado de cualquiera de sus lados es igual a la suma de
los cuadrados de los otros dos lados, menos el doble producto de estos lados por el coseno
del ángulo comprendido entre ellos. Esto es:
Este teorema se aplica cuando
en un triángulo dado se conocen:
•CASO I: Dos lados y el ángulo
comprendido entre ellos.
•CASO II: Los tres lados del triángulo.
a
c
Teorema: En cualquier triángulo ABC, la
relación entre un lado y el seno del ángulo
opuesto, es constante.
Éste teorema se aplica cuando en un triángulo
dado se conocen:
•CASO I: Dos ángulos y el lado opuesto a uno
de ellos.
•CASO II: Dos ángulos y el lado entre ellos.
•CASI III: Dos lados y el ángulo opuesto a uno
de ellos.
2 2 2
2 2 2
2 2 2
2 cos
2 cos
2 cos
a b c bc
b a c ac
c a b ab



  
  
  

39. 30.3 40.4 62.6
23.65 32.3 124.05
7 6 9
a b c
a b c
  
  
     
  
2 3 4 5 6
6 6 6 6 6 6
2 5
0
6 3 2 3 6
30 60 90 120 150 180
3
4 2 4
     
    

  

Cálculo de funciones trigonométricas para ángulos comunes.
2
n
0 1 2 3 4
sin 0 ½ 2
2
3
2
1
cos 1 3
2
2
2
½ 0
tan 0
1
3
1 3 Ind
0 0 30° 45° 60° 90°
radianes 0 6

4

3

2

sin
cos
0° 30° 45° 60° 90°
0 1 2 3 4
4 3 2 1 0
2
tan
0° 30° 45° 60° 90°
0 1 2 3 4
4 3 2 1 0
I cuadrante todas (+)
II cuadrante sin, cosec (+)
III cuadrante tan, cotan (+)
IV cuadrante cos, sec (+)
ABC=

40. 1 1 2
sec
cos 3 3
2
1
csc
sin
  

Cat. Opuesto Cat. Adyacente
sin cos=
Hipotenusa Hipotenusa
Cat. Opuesto 1
tan cot=
Cat. Adyacente tan
x y
r r
x y
y x


r x
sec= csc=
r r
y x
Encuentre el valor de cada una de las seis funciones trigonométricas, si el punto P(-3,4)
pertenece al lado terminal del ángulo asociado y sus ángulos internos.
a = 4
C
c
A
B
b=3

41. Ejemplos:
Calcular la altura h del siguiente triángulo rectángulo.
tan 60
340
h
 
Un cable se amarra a 12 m de la base de un mástil y el cable forma un ángulo de 15° con el
suelo. ¿Cuánto mide dicho cable?
2 2 2
2 2 2
12
sin15
46.3644
r x y
x r r r
x
   

60°
340 m
h=?
12m
15°
9
6
10
y 3
7

42. IDENTIDADES TRIGONOMÉTRICAS.
2 2 2 2 2 2
1 1 1 1
sin cos tan cot
csc sec cot tan
1 1 sin cos
sec csc tan cot
cos sin cos sin
sin cos 1 sec tan 1 csc cot 1
   
   
 
   
   
   
   
   
     
Ejercicios:
2 2
2
2
2 2
2
2
2
2 2
2 2
2
2
2
1.-sin cos sin csc
1
2.- cos 1
csc
3.- tan sin csc sec
cos
4.- 1 csc
sin
5.-sin cos cos sec
6.- tan tan cot sec
sin
7.- 1 sec
cos
x x x x
x
x
x x x x
x
x
x
x x x x
x x x x
x
x
x
 
 
 
 
 
 
 
2
2
2 2
2
2
2
2
2
1
8.-sin 1
sec
9.-tan cos cos 1
sin
10.-sin 1
tan
1
11.- tan
cos csc
12.-cos csc cot
1
13.- cot
sin sec
1
14.- 1 csc
tan
x
x
x x x
x
x
x
x
x x
x x x
x
x x
x
x
 
 
 



 
Senos y cosenos.
2 2
2
2
2
2
2
2
2
sin 1
sin sec cos 1
cot csc
1 1
sec
cot sin csc
1
csc
sec
1 cot 1 tan
csc sec
sin 2 2cos
2 2 tan
1 sin
x
x x x
x x
x
x x x
sen x senx x
x
y y
y y
x x
x
x
  
 
 
 


 

2
2
2 2 2 2
1 1
sec cos
cos sec
cot sin cos csc
x x
x x
x x x x
  
  
TAREA
TAREA

43. FUNCIONES TRIGONOMÉTRICAS INVERSAS.
ECUACIONES TRIGONOMÉTRICAS.
1 1 1 1 1 1
sin cos tan
sin cos tan
x x x
x x x
     
Obtener la solución de las ecuaciones siguientes cuando
0 1 tan2 3 0 2cos2 1 0
2
 x   x   x  
2
2
cot 1 0 0 x
2sin cos 1 0 0 2
Obtenga todos los valores de en [0,2 )
tan 3 1
x
t t t
x
x



   
    

Arco coseno
Arco seno
Arco tangente

44. SISTEMAS DE ECUACIONES Y DESIGUALDADES.
2
5 5 2 7
4
6 7 3 0
6
7
3
x x
x
x x
a
b
c
  

  


 
Si a y b exactamente uno de los tres siguientes enunciados es verdadero:
y entonces
5 y 5
a b b c a c
x y
x y
  
 

Propiedades de < si a, b y c son  :
i) Si a < b, entonces a+c < b+c (propiedad de suma)
ii) Si a < b, entonces a-c < b-c (propiedad de resta)
iii) Si a < b y c > 0, entonces ac < bc (propiedad de la multiplicación)
iv) Si a < b y c < 0, entonces ac > bc (propiedad de multiplicación)
3 8 7
5
x
x
 

7
4
7
3
{ | 7 }
3
[ 7 , )
3
x
x
x
x x


 
 
 
3 4 7 15
3 4 7 4 7 15
1 2
( 1,2]
x
x x
x
  
   
  

0 5
2
2
2
2 8 0
( 2)( 4) 0
( , 2)( 2, 4)(4, )
12 15
2 15 0
( 5)( 3) 0
( , 5)( 5,3)(3, ) conjunto de soluciones: ( 5,3)
| 3 5 | 9
3 5 9 (3 5) 9
3 4 3 5 9
4 3 14
3
14 conju
3
x x
x x
x x
x x
x x
x
x x
x x
x x
x
  
  
   
 
  
  
    
 
    
   
  
  nto{4 , 14 }
3 3


45. 1 1 1
2 2 2
2 3 6 3 5
5 3 10 2 4
ax by c
a x b y c
a x b y c
x y x y
x y x y
 
  
 
   
   
4 3 4 2 3 8
2 3 2 0 5 3 4 4
2 2 2 6 4 5 12
x y z x y z
x y z x y z
x y z x y z
     
     
     
2 2 2
2 2
2 2
=4 +y =25
x+y=3 3 4 25
4 +xy+y =6 *
2 8
y x x
x y
x
x xy y
 
  
2 2
2 2
4 6
10 7 0 (6 )(2 ) 0
5 2
x xy y
x xy y x y x y
y x y x
  
     
   

46. MATRICES.
Una matriz fila está constituida por una sola fila (2, 3, -1)
2 1 0 1 1 3 5
, B= , C=
3 2 4 2 2 1 1
A
      
      
       
a)
4 4 4 16 16
;
8 1 6 25 39
AB ABC
     
     
    
b)  
9
4 2
2 3
1 2 1 5 15
2 2 2
1 3
11 9
2
t B A C B A
                
           
 
c) 2 2 2 1 4 4 2
No se puede
12 1 8 8
A B C
     
      
   
2 2 2
2
2 6 3 1 1 1
0 9 5 2 4 2
6 2 1 3 5 7
; ( ) 2
( ) ( )( )
no es conmutativa
A B
AB BA A B A AB B
AB BA A B A B A B
   
   
      
       
  
   
a) ABC b)  1 
2
t C B  A c) 2 2 2 A ,B ,C

47. DETERMINANTES.
Sea A una matriz cuadrada de orden n. Se define como determinante de A (denotado como
|A|, det(A) ó A  ) a la suma de los n productos formados por n-factores que se obtienen al
multiplicar n elementos de la matriz de tal forma que cada producto contenga un solo
elemento de cada fila y columna de A.
Esto significa, que un determinante es un valor numérico x que está relacionado con una
matriz cuadrada y que sigue ciertas reglas para su cálculo.
Regla de Sarrus.
Determinante de segundo orden es el producto de los elementos de la diagonal principal
menos el producto de los elementos de la diagonal secundaria.
11 12
11 22 21 12
21 22
11 12 13
21 22 23 11 22 33 21 32 13 31 12 23 31 22 13 21 12 33 11 32 23
31 32 33
det( )
det( )
a a
A a a a a
a a
a a a
A a a a a a a a a a a a a a a a a a a a a a
a a a
  
      
Propiedades de los determinantes.
1. Si todos los elementos de una columna o de un renglón son cero, entonces el
determinante es cero.
2. El determinante de la matriz A es el determinante de la matriz A t .
3. Si cada elemento de un renglón o una columna es multiplicado por un
escalar k, el determinante es también multiplicado por k.
4. Si se intercambian dos renglones o columnas el signo del determinante
cambia.
5. Si un renglón o columna se traslada P renglones o columnas entonces el
determinante obtenido es igual a ( 1) p  .
6. Si dos renglones o dos columnas son iguales, entonces el determinante es
cero.
Menor de un elemento.
Se define el menor de un elemento ij a al determinante que resulta de eliminar el renglón i y
la columna j.

48. Cofactores.
Se define el cofactor de un elemento ij a , el cual se denota A ij como:
Aij = ( 1) i j
ij M  
Es decir, el cofactor es igual al menor multiplicado por 1 o -1 dependiendo si la suma de los
dos subíndices es par o impar respectivamente.
11 12 13
21 22 23 11 11 12 12 13 13
31 32 33
22 23 21 23 21 22
11 12 13
32 33 31 33 31 32
det( )
a a a
A a a a a A a A a A
a a a
a a a a a a
a a a
a a a a a a
   
 
Matriz adjunta.
 
1
( )* ( )*
det( )
T T A Adj A
A

Ejemplos:
2 1 0
3 5 4 8 9 1
2 4 0 3 5 10 254
2 4 3 7 0 0
1 7 8

 
     



49. Menor de un elemento.
22
31
23
11
12
13
1 5 3
2 1 4
3 10 2
32
23
56
1 0 1
2 5 4
3 10 2
= 30
=16
A =-35
1 2 8
det( ) 6 4 5 39
2 1 3
M
M
M
A
A
A
 
 



 
  


   


50. LÍMITES Y DERIVADAS.
*
Sea a un punto de un intervalo abierto, sea f una función definida en todo el intervalo
excepto posiblemente en a, y sea L un número real. Entonces:
lim ( )
x a
f x L


Significa que para todo > 0 existe un  > 0 tal que sí 0 | x a | , entonces
| f (x)  L|
*De forma intuitiva se puede definir el límite de una función en un punto como el valor al
que se aproxima la función cuando la variable independiente se acerca al punto.
Propiedades de los límites.
- Límite de una constante.
lim lim
x a x a
k k x a
 
 
- Límite de una suma.
lim[ ( ) ( )] lim ( ) lim ( )
x a x a x a
f x g x f x g x
  
  
- Límite de un producto.
lim[ ( ) ( )] lim ( ) lim ( )
x a x a x a
f x g x f x g x
  
  
- Límite de un cociente.

51. ( ) lim ( )
lim Si lim ( ) 0
( ) lim ( )
x a
x a x a
x a
f x f x
g x
g x g x

 

 
   
 
- Límite de una potencia.
 ( ) lim ( ) lim ( ) lim ( ) x a Si ( ) 0
g x g x
x a x a
f x f x  f x
 
   
- Límite de un logaritmo.
limlog ( ) log lim ( ) Si 0 y ( ) 0 a a
x a x a
f x f x a f x
 
    
 
Operaciones con infinito (indeterminaciones.)
Infinito más un número
  k = 
0
0
0
.
( ) si 0
0 .
0 0
0
0
0 in .
0
.
1
0 .
.
ind
k k
ind
k
k
k
k
d
ind
k
ind
ind
    
   
     
    
  

 


  

 



 
0 0 si k>0
si k<0
si k>0
0 si k<0
0 0
0
1 .
k
k
ind






 

 

lim ; lim
x a x a
k k x a
 
 

52. Ejercicios.
3 8
2
3 2
2
2
3 2
2
0
1
3
3 2
3 2 3
*lim8 *lim3
2 7
*lim =-
5 2 4
* lim [0, )
9
*lim D[ , 2) (2,3) (3, )
5 6
*lim( ) 1
*lim5 ln 0
1 1
*lim 0
3
27 0 ( 3)( 3 9
*lim lim
9 0
x x
x
x
x
x
x
x
x
x x
x
x x
x
x
x x
x e
x x
x
x x x x
x
 






 

 


   
 
 

 
 
   


2 2 2
4
4
) 9
( 3)( 3) 2
2 0 ( 2)(1 1) ( 2)(1 1)
*lim lim
1 1 0 (1 1)(1 1) 1 ( 1)
( 2)(1 1) ( 2)(1 1)
(1 1)
1 1 ( 2)
5 1 0 1
*lim
2 3 2 0 2
x x
x
x x
x x x x x
x x x x
x x x x
x
x x
x
x
 


 
      
 
       
     
    
   
  
  
  
1 0
1 0
...
lim
...
n
n
x m
m
a x a x a
 b x b x b
  
  
5
4
2
4
2
2
5 1
* lim
1
5
*lim 0
2 3
3 5 3
*lim
5 3 1 5
x
x
x
x x
x
x
x
x
x x



  
  
 
 
 
 
 
 
  
0 si m>n
si m=n
si m < n

53. Tarea:
1. Si 2 f (x)  x  2 y g(x) 1
x
 . Calcular:
a)
3
lim( )( )
x
f g x


b)
3
lim( )( )
x
f g x


c)
3
lim( )( )
x
f g x


d)
3
lim( / )( )
x
f g x

2. Calcular el límite de la función
3 2
2
( 2 6 12)
( )
( 3 10)
x x x
g x
x x
  

 
cuando x2 .
3. Calcular el límite de la función
2 (3 4 )
( )
x x
f x
x

 cuando x0 .

54. DERIVADAS.
Sea f una función definida en un intervalo abierto que contiene a a. La derivada de f en a,
denotada por 1f (a) está dada por:
1
0
1
0
( ) ( )
( ) lim
( )
( ) lim
h
x
f a h f a
f a
h
f f a
f a
x a


 




La derivada es el resultado de un límite y representa la pendiente de la recta tangente a la
gráfica de la función en un punto.
Una función f es derivable en un intervalo cerrado [a,b] si lo es en el intervalo abierto (a,b)
y los límites.
0 0
( ) ( ) ( ) ( )
lim y lim existen
h h
f a h f a f b h f b
h h    
   
y
x
a x
1
0
( ) ( )
( ) lim
h
f x h f x
f x
h
como una función

 


55. Ejemplo 1:
2
0
( ) ( )
( ) 3 5 4 Encontrar ( ) lim
h
f x h f x
f x x x f x
 h
 
   
a) 1f (x)
b) 1 1 f (2), f ( 2)
1
1 1
2
4 3 2
7 2
7 3
7
2 2 2 2
81
7
( ) 6 5
(2) 7 ; ( 2) 6 2 5
( ) 2 5
( ) 2 4
1
lim
2 300
entre x
4
lim 2 3 2 3 2 3 2 3 2
2
81
lim 18
9
( 1)( 2)
lim 1
( 3)( 4)
lim
x
x
x
x
x
f x x
f f
f x x
f x x x x
x x
x x
x x x x x x x x
x
x
x x
x x





 
    
 
   
  

  
           



 

 
2
2 3
49
x
x
 

2
1
0
2
1
0
2 2 2
1
0
2
1
0 0
1 1
( ) ( )
( ) lim
3( ) 5( ) 4 (3 5 4)
( ) lim
3 6 3 5 5 4 (3 5 4)
( ) lim
6 3 5
( ) lim lim6 3 5 6 5
( ) [ ( )] [ ( )]
h
h
h
h h
f x h f x
f x
h
x h x h x x
f x
h
x xh h x h x x
f x
h
xh h h
f x x h x
h
dy d
f x Dx f x Dxy y f x
dx dx



 
 

        
  
          
 
     
    
Como función

56. Reglas para determinar derivadas.
( ) 0
( ) 1
Dx c derivadas
Dx x


Si n es un entero positivo entonces, Dx( xn ) = n 1 nx 
2
1
[ ( )] [ ( )]
[ ( ) ( )] [ ( )] [ ( )]
[ ( ) ( )] ( ) [ ( )] ( ) [ ( )]
( ) ( ) [ ( )] ( ) [ ( )]
( ) [ ( )]
( )n n
Dx cf x cDx f x
Dx f x g x Dx f x Dx g x
Dx f x g x f x Dx g x g x Dx f x
f x g x Dx f x f x Dx g x
Dx
g x g x
Dx x nx 

  
 
  
  
 
  
1.- 2 f (x) 10x 9x 4  20x 9
5.- 3 2 4 2 f (x)  (x 7)(2x 3) 10x 9x 28x
9.- 2
4 5 23
( )
3 2 (3 2)
x
f x
x x

 
 
3.- 2 4 3 f (s) 15 s  4s 5s  18s 20s
7.- 2 4 5 2 h(r)  r (3r 7r  2) 18r 21r 4r
22.- 2 3
1 1 1
p(x) 1
x x x
   
4
( ) 4
4
f x x
x
 

 
x 9
2 13
3 401
100
f(x) 8 12 400
 
x 7
2 15
4 399
100
f(x) -8 -16 -400

57. 2
4
( )
5 6
f x
x x

 
2
( 2)( 3)
3 2 6
2; 3
x x
x x x
x x
 
  
 
x 3
2 7
4 199
100
f(x) 5.3 12.8 396
x 7
2 13
4 301
100
f(x) 5.3 12.8 396
x 7
3 2001
1000
f(x) -18 -4004
x 11
4 2999
1000
f(x) -21 -4004
2
2 2
2 2
2
8 3 6
( ) ; ( )
1 2 4
4 4 3 3
( ) ó ( ) ó
25 ( 5)( 5) 2 32 2( 4)( 4)
16
( )
3
x
f x f x
x x x
x x x
f x f x
x x x x x x
x
f x
x

 
  
 
     




58. CONVERSIONES DE UNIDADES.
180
1 radianes 1 radián=
180
150 5 7 7(180)
315
180 6 4 4
225 5 180
60
180 4 3 3
360 (180)
2 90
180 2 2


 
 



 
   
 

   


   


   

TEOREMA DE PITÁGORAS.
El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
2 2 2
2 2
2 2
c a b
b c a
a c b
 
 
 
Calcular la altura (h) del siguiente triángulo rectángulo y la hipotenusa.
a
op
c=hipotenusa
body
sin tan cos
a a b
c b c
     
1
1
1
sin csc
cos sec
tan cot
c
a
c
b
b
x
a
 





 
 

h=
?
60°
Hip.=?
340 cm
2 2
1 1
1 1
tan 60 ; tan 60 (340) 588.9
340
(340 ) (588.9 ) 680
sin ( ) sin (588.9) 680
cos ( ) cos (340) 680
h
h cm
c cm cm cm
c a cm
c b cm
 
 
 
 
    
  
  
  

59. Un cable se amarra a 12m de la base de un mástil y el cable forma un ángulo de 15° con el
suelo. ¿Cuánto mide dicho cable?
12 12
sin15 ; 46.36
0 sin15
m m
x m
x
   

Una escalera está apoyada contra la pared de un edificio y su base se encuentra a una
distancia de 12 ft del edificio. ¿A qué la altura está el extremo superior de la escalera y cuál
es la longitud de esta si el ángulo que forma con el suelo es de 70°?
tan 70 ; tan 70 (12 ) 32.9
12
12 12
cos70 ; 35.1
4 cos70
x
x ft ft
y ft
    
   

x
12m
15°
?
?
70°
12 ft

60. PASANDO A SENOS Y COSENOS.
2
2
2 2
2
sec 1 1 1 cos
* sec ; csc ; cot
csc cot csc 1 sin
1
cos
1 1 sin sin ;
sin cos cos cos
sin
1 1 cos 1 1
* sec cot csc sec
cot sin csc sin sin cos
1 1 1
cos 1 cos
sin
sin sin
x x
x x x
x x x x senx
x
x x
x x x x
x
x
x x x
x x
x
x x
   
 
    
 
2 2
2 2 2 2
2 2 2 2
sin cos 1 1 1
cos cos cos cos
1 1
*sec csc sec csc (sin cos ) sec csc
cos sin
1 1 1 1
(sin cos )
cos sin cos sin
sin cos (sin cos )
cos sin sin cos
1
*sin cos sec tan sec
cos
x x
x x x x
x x x x x x x x
x x
x x
x x x x
x x x x
x x x x
x x x x x
x

  
    
  


   
2
2 2
2 2
2 2
2 2 2 2
2 2
sin
tan
cos
1 sin
sin cos
cos cos
1 sin cos
sin cos cos sin 1 1
cos cos
x
x
x
x
x x
x x
x x
x x x x
x x

  

      

61. Ecuaciones trigonométricas.
1
2
1 1
2
6
2sin 1=0 0
sin
x x
x
x 


  


2 1
2
1
3
*tan 3 0 0 x
tan 3
tan 3
x
x
x
x 


   



2 2
2 1
2
3
4 4 4
1
*2cos 1 0 cot 1 0 0 x
cos cot 1 1
1
cos cot 1 { , }
2
1
cos cot
2
x x
x x
x x
x x
  


     
   
 
 3
4
4
1
x


 

*Obtener las soluciones de la ecuación 0  x  2
2
2 1 5
2 3 3
2
2
5
3 3
1
2
2sin cos 1 0
2(1 cos ) cos 1 0 ( , )
2 2cos cos 1 0 1
2cos cos 1 0
(2cos 1)(cos 1) 0 { , , }
2cos 1 0 cos 1 0
cos cos 1
x x
x x
x x
x x
x x x
x x
x x
 
 


  
    
     
  
   
   
  

62. *Obtener el conjunto de soluciones de
2
2
2
5
4 4
5
4 4
sec tan 1 0 2
(1 tan ) tan 1
tan tan 0
tan (tan 1) 0
tan 0 tan 1
0; ; 2 ,
{0, ,2 , , }
x x x
x x
x x
x x
x x
x x x x
x
 
 

 
 
   
  
 
 
 
   

*Obtenga todos los valores de x en [0, 2 ) para los que tan3x 1
0 2 ;0 3 6
tan 3 1
1 5 9 13 17 21
, , , , , ,
4 4 4 4 4 4
x x
x
 
     
   
