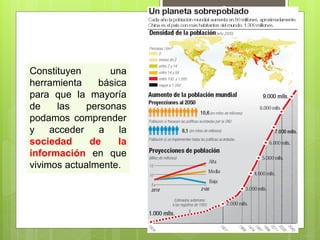
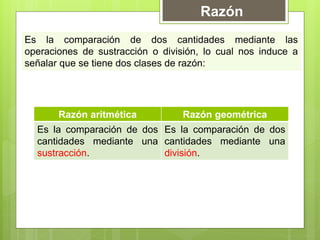
El documento presenta las razones para estudiar y aprender matemáticas. Primero, las matemáticas son una de las máximas expresiones de la inteligencia humana y han sido fundamentales en el desarrollo cultural y tecnológico a lo largo de la historia. Segundo, las matemáticas se aplican universalmente en otras ciencias y en diversas actividades humanas como la ingeniería y la tecnología. Tercero, las matemáticas constituyen una herramienta básica para comprender la sociedad de la información moderna.

1. Razones
Prof.: Christiam Huertas
(X – 14)

2. Matemática

3. ??????

4. ¿Por qué estudiar y aprender matemáticas?

5. 1
Son una de las máximas expresiones de la inteligencia
humana y un magnífico ejemplo de las creaciones
intelectuales.
𝒄
𝒃
𝒂
𝑐 2 = 𝑎2 + 𝑏 2
Pitágoras de Samos (580 aC – 495 aC)
Fue un filósofo y matemático griego,
considerado el primer matemático puro

6. 2
Constituyen un eje
central de la historia de
la cultura y de las
ideas del hombre a
través del tiempo.
El Partenón. Esta
construcción es uno de
los ejemplos más claros
del saber en geometría
por parte de los
matemáticos y arquitectos
griegos.

7. 3
Gracias a su universalidad, se aplican en las otras ciencias,
de la naturaleza y sociales, se emplean en los distintos tipos
de actividad humana, de modo tal que resultan
fundamentales en el desarrollo y el progreso de los
pueblos.

8. 4
Constituyen una
herramienta básica
para que la mayoría
de las personas
podamos comprender
y acceder a la
sociedad de la
información en que
vivimos actualmente.

9. Las matemáticas se aplican
Para diseñar y desa- Para realizar sistemas Para diseñar y cons-
rrollar diversos tipos de control, por ejemplo, truir automóviles, ca-
de dispositivos, por de los satélites que rreteras, aviones, ru-
ejemplo, los compo- permiten la comunica- tas aéreas, edificios,
nentes de las compu- ción y la transmisión de puentes, etc.
tadoras. los programas de tele-
visión, o la conexión
entre computadoras y
entre teléfonos celula-
res.

10. Razones
El concepto de razones y proporciones que estudiaremos en
esta sección es fundamental para el desarrollo y vinculación
de las matemáticas con la realidad.
El objetivo es la
solución de problemas
cotidianos que implican
razones y proporciones
y sus aplicaciones en
diferentes áreas del
conocimiento tales
como la ingeniería, la
arquitectura, la química
y los negocios entre
otros.

11. 500 m
Razón
En la vida cotidiana es
común que comparemos
nuestro peso, altura, 400 m
fuerza, salario, horas de
trabajo y productividad
con los de otras
personas; los precios de 300 m
diferentes productos.
2 1
500 m − 300 m = 200 m 200 m
500 m 5
=
300 m 3 100 m

12. Razón
Es la comparación de dos cantidades mediante las
operaciones de sustracción o división, lo cual nos induce a
señalar que se tiene dos clases de razón:
Razón aritmética Razón geométrica
Es la comparación de dos Es la comparación de dos
cantidades mediante una cantidades mediante una
sustracción. división.

13. Razón aritmética
Es la comparación de dos cantidades mediante la sustracción
y consiste en determinar en cuanto excede una de las
cantidades a la otra.
𝑎− 𝑏= 𝑟
Donde:
𝑎: Antecedente
𝑏: Consecuente
𝑟: Valor de la razón aritmética.

14. Razón aritmética
Ejemplo: Los automóviles
A y B se desplazan con
velocidades de 24 m/s y
20 m/s respectivamente,
comparemos sus velocida-
des.
Razón aritmética Valor de la RA
24 m/s − 20 m/s = 4 m/s
Antecedente Consecuente
Interpretación:
• La velocidad de A es mayor en 4 m/s que la velocidad de B.
• La velocidad de A excede en 4 m/s a la velocidad de B.
• La velocidad de B es menor en 4 m/s que la velocidad de A.
• La velocidad de B es excedida en 4 m/s por la de B.

15. Razón aritmética
Ejemplo: Si la edad de Ana
es de 30 años y la de Beto
es de 10 años, entonces
comparemos dichas edades.
Razón aritmética Valor de la RA
𝐀𝐧𝐚 𝐁𝐞𝐭𝐨
− = 20 años
30 años 10 años
Antecedente Consecuente
Interpretación:
• La edad de Ana es mayor que Beto en 20 años.
• La edad de Ana excede a la de Beto en 20 años.
• La edad de Beto es excedida en 20 años por la edad de
Ana.

16. Razón aritmética
Observación:
Cuando en un texto aparece la palabra excede o excedido,
hace referencia a la sustracción.
Por ejemplo:
1. A excede a B en 8 quiere decir: A – B = 8.
2. A es excedido por B en 8 quiere decir: B – A = 8.

17. Razón geométrica
Es la comparación de dos cantidades mediante la división y
consiste en determinar en cuantas veces una de las
cantidades contiene la unidad de referencia.
𝑎
= 𝑘
𝑏
Donde:
𝑎: Antecedente
𝑏: Consecuente
𝑘: Valor de la razón geométrica.

18. Razón geométrica
Ejemplo: Si la edad de Ana
es de 30 años y la de Beto
es de 10 años, entonces
comparemos dichas edades.
Razón geométrica
Antecedente → 30 años 3
=
Consecuente → 10 años 1
Valor de la RG
Interpretación:
• La edad de Ana es el triple de la edad de Beto.
• A es a B como 3 es a 1.
• A y B están en la relación de 3 a 1.
• Las edades de Ana y Beto son proporcionales a 3 y 1.
• A es tres veces B.

19. Razón geométrica
Observaciones:
• A es 2 veces B → A = 2B.
• A es 2 veces más que B → A = 3B.
Pues,
A = B + 2B = 3B.
2 veces más
www.aritmethica.blogspot.com