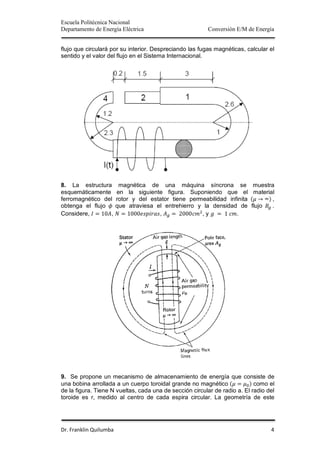
1. El documento presenta 10 ejercicios de circuitos magnéticos para ser resueltos. Los ejercicios involucran el cálculo de flujo magnético, inductancia, reluctancia y densidad de campo magnético para diferentes configuraciones de circuitos magnéticos con núcleos de permeabilidad finita e infinita. 2. Los ejercicios piden calcular valores como flujo total, concatenaciones de flujo, inductancia, reluctancia, densidad de campo magnético e inductancia mutua para circuitos con diferentes dimensiones geométricas, número de esp

1. Escuela Politécnica Nacional
Departamento de Energía Eléctrica Conversión E/M de Energía
Dr. Franklin Quilumba 1
Ejercicios circuitos magnéticos
1. Se tiene un circuito magnético con un solo entrehierro, como en la figura. Las dimensiones del núcleo son:
Área de la sección transversal 퐴푐=1.8×10−3푚2
Longitud media del núcleo 푙푐=0.6푚
Longitud del entrehierro 푔=2.3×10−3푚
N = 83 vueltas
Suponga que la permeabilidad del núcleo es infinita (μ →∞) y desprecie los efectos de dispersión magnética y de abombamiento. Calcule, para una corriente de i = 1A, a) el flujo total 휙, b) las concatenaciones de flujo λ de la bobina, y c) la inductancia L de la bobina.
2. Repita el problema anterior para una permeabilidad finita del núcleo, igual a 휇=1500휇0
3. El circuito magnético de la figura tiene las siguientes dimensiones: 퐴푐=9푐푚2, 퐴푔=9푐푚2, 푔=0.050푐푚, 푙푐=30푐푚, y 푁=500푒푠푝푖푟푎푠. Supóngase el valor 휇푟=70000 para el hierro. Si la inducción magnética en el núcleo es igual a 1T, calcule:
a) Reluctancias ℛ푐 y ℛ푔
b) Flujo 휙 que recorre el núcleo.
c) Intensidad de corriente que recorre la bobina.

2. Escuela Politécnica Nacional
Departamento de Energía Eléctrica Conversión E/M de Energía
Dr. Franklin Quilumba 2
4. Suponga que el circuito magnético del problema 2 tiene la siguiente curva de magnetización DC. Calcule la corriente i para una densidad de campo magnético en el núcleo 퐵푐=1푇.
5. El circuito magnético de la figura está realizado con material ferromagnético cuya curva de magnetización responde a la siguiente expresión:
퐵= 2∙10−3∙퐻 1+10−3∙퐻
B: Teslas, H: A-v/m.

3. Escuela Politécnica Nacional
Departamento de Energía Eléctrica Conversión E/M de Energía
Dr. Franklin Quilumba 3
El entrehierro es de 1 mm, la longitud magnética media de la estructura es 1 m y la sección transversal es uniforme e igual a 20푐푚2. Calcule la densidad de campo magnético en el entrehierro.
6. El circuito magnético de la figura tiene una bobina de N espiras, arrollada en un núcleo magnético de permeabilidad infinita con dos entrehierros en paralelo de longitudes 푔1 y 푔2 y áreas 퐴1 y 퐴2, respectivamente. Si se desprecia el efecto de borde (abombamiento) en el entrehierro, calcule:
a) Inductancia del devanado.
b) Densidad de flujo 퐵1 en el entrehierro 1 si por el devanado circula una corriente i.
7. El circuito magnético de la figura de sección circular, expresado en cm., está formado por cuatro materiales de distinta permeabilidad magnética, donde 휇푟1=5000, 휇푟2=6000, y 휇푟4=7000. El material 1 tiene arrollada una bobina de 10000 espiras, recorrida por una intensidad de 10 A. Aparecerá en el circuito un

4. Escuela Politécnica Nacional
Departamento de Energía Eléctrica Conversión E/M de Energía
Dr. Franklin Quilumba 4
flujo que circulará por su interior. Despreciando las fugas magnéticas, calcular el sentido y el valor del flujo en el Sistema Internacional.
8. La estructura magnética de una máquina síncrona se muestra esquemáticamente en la siguiente figura. Suponiendo que el material ferromagnético del rotor y del estator tiene permeabilidad infinita (휇→∞), obtenga el flujo 휙 que atraviesa el entrehierro y la densidad de flujo 퐵푔. Considere, 퐼=10퐴, 푁=1000푒푠푝푖푟푎푠, 퐴푔= 2000푐푚2, y 푔 = 1 푐푚.
9. Se propone un mecanismo de almacenamiento de energía que consiste de una bobina arrollada a un cuerpo toroidal grande no magnético (휇=휇0) como el de la figura. Tiene N vueltas, cada una de sección circular de radio a. El radio del toroide es r, medido al centro de cada espira circular. La geometría de este

5. Escuela Politécnica Nacional
Departamento de Energía Eléctrica Conversión E/M de Energía
Dr. Franklin Quilumba 5
dispositivo es tal que se puede considerar que el campo magnético es cero en cualquier lugar fuera del toroide. Suponiendo que a << r, se puede considerar que el campo H dentro del toroide está dirigido alrededor de éste, y tiene magnitud uniforme
rNiH π2=
Calcule la inductancia L de la bobina.
10. Un sistema de tres bobinas sobre un núcleo ideal se muestra en la figura, donde 푁1=푁3=2푁2=500 푣푢푒푙푡푎푠, 푔1=2푔2=2푔3=4푚푚, y 퐴=1000푚푚2. Calcúlese a) la autoinductancia de la bobina 푁1 y b) la inductancia mutua entre las bobinas 푁2 y 푁3.