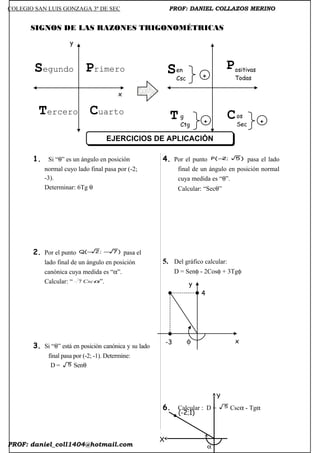
El documento presenta información sobre las razones trigonométricas de ángulos en posición normal. Explica que un ángulo está en posición normal cuando su lado inicial pasa por el eje de abscisas positivo y su lado final está en el primer o cuarto cuadrante. Luego, proporciona ejemplos numéricos para calcular valores trigonométricos dados puntos y ángulos. Finalmente, incluye ejercicios de aplicación para que el lector practique el cálculo de funciones trigonométricas.

1. RAZONES TRIGONOMÉTRICAS DE
ÁNGULOS EN POSICIÓN NORMAL I
RAZONES TRIGONOMÉTRICAS DE
ÁNGULOS EN POSICIÓN NORMAL I
COLEGIO SAN LUIS GONZAGA 3º DE SEC PROF: DANIEL COLLAZOS MERINO
SISTEMAS DE COORDENADAS RECTANGULARES
Donde:
x : Eje de Abscisas
y: Eje de Ordenadas
IC: Primer Cuadrante
IIC: Segundo Cuadrante
IIIC: Tercer Cuadrante
IVC: Cuarto Cuadrante
O : Origen del Sistema
radio vector .
Es el segmento de recta dirigido (flecha) que parte del origen hacia un punto
cualquier del sistema; su longitud o módulo esta representado por “r”.
a : Abscisa del Punto P
b : Ordenada del Punto P
(a;b) : Coordenadas del Punto P
Donder: Longitud del Radio Vector
REGLA:
Ángulo en posición normal .
DEBEN CUMPLIR LAS SIGUIENTES CONDICIONES:
Donde:
α, β ∧ θ son ángulos en posición normal.
L.I.: Lado Inicial
L.F.: Lado Final
Las Razones Trigonométricas de un ángulo en posición normal son independientes del
sentido de giro o el número de vueltas que pudiera realizar.
PROF: daniel_coll1404@hotmail.com
r2
= a2
+ b2
También son llamados
∢s en posición
canónica o estándar.
+
+
–
– IVCIIIC
ICIIC
y
x
O
x
y
α
β
θ
y
x
| b |
| a |
P(a;b)

2. COLEGIO SAN LUIS GONZAGA 3º DE SEC PROF: DANIEL COLLAZOS MERINO
SIGNOS DE LAS RAZONES TRIGONOMÉTRICAS
1. Si “θ” es un ángulo en posición
normal cuyo lado final pasa por (-2;
-3).
Determinar: 6Tg θ
2. Por el punto )7;2(Q −− pasa el
lado final de un ángulo en posición
canónica cuya medida es “α”.
Calcular: “ αCsc7 ”.
3. Si “θ” está en posición canónica y su lado
final pasa por (-2; -1). Determine:
D = 5 Senθ
4. Por el punto )5;2(P − pasa el lado
final de un ángulo en posición normal
cuya medida es “θ”.
Calcular: “Secθ”
5. Del gráfico calcular:
D = Senφ - 2Cosφ + 3Tgφ
6. Calcular : D = 5 Cscα - Tgα
PROF: daniel_coll1404@hotmail.com
EJERCICIOS DE APLICACIÓNEJERCICIOS DE APLICACIÓN
x
y
Segundo Primero
Tercero Cuarto
S P
T C
en
Csc
ositivas
Todas
g
Ctg
os
Sec
+
+ +
Y
X
α
(-2;1)
x
y
4
-3 φ

3. COLEGIO SAN LUIS GONZAGA 3º DE SEC PROF: DANIEL COLLAZOS MERINO
7. Del gráfico, calcular:
θθ TgCosE 2611 −=
8. Del gráfico calcular:
ββ CtgSecE 45 +=
9. De la figura, hallar : 5Senβ +
13Cosα
10. Del gráfico, hallar :
E = Senα - 2Ctgα + Cosα
11. Del gráfico, determine : D = Tgθ
+ Tgα
12. A que cuadrante pertenece “θ” si:
Tgθ < 0 ∧ Cosθ > 0
13. A que cuadrante pertenece φ si:
Senφ < 0 ∧ Secφ < 0
PROF: daniel_coll1404@hotmail.com
x
y
)2;3(−
θ
x
y
β
(1; -2)
-4
-3
5
X
-3
Y
α
θ
X
Y
(-3;-4)
(12;-5)
α
β
Y
X
-3
4
α

4. COLEGIO SAN LUIS GONZAGA 3º DE SEC PROF: DANIEL COLLAZOS MERINO
14. Del gráfico, calcular: D =
Tgα.Ctgθ
15. De la figura, calcular : E = 13Tgθ
16. Del gráfico, hallar Cosθ
17. Indicar el signo de cada expresión:
I. Sen100º.Cos200º
II. Tg190º.Ctg320º
III. Sec200º.Csc350º
18. Si: IIICSen ∈∧−= αα
3
2
Calcular: )(5 αα SecTgE +=
19. Si: IVCCtg ∈∧−= θθ
2
3
Calcular: θθ SenSecE 721 +=
20. Del gráfico calcular “Tgφ”
21. Del gráfico calcular “Tgβ”
(AB = BC)
PROF: daniel_coll1404@hotmail.com
x
y
37º
φ
Y(a;8)
10
θ
-5
7
X
Y
α
θ
(-5;-12)
17
X
Y
(4;a)
θ
x
y
A B
-1
C
β
3