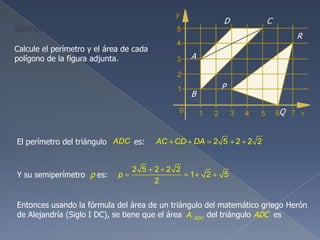
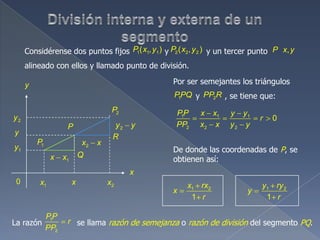
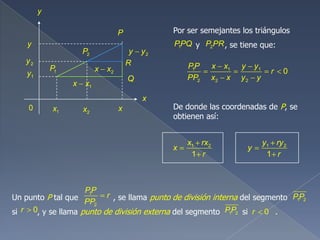
El documento explica cómo calcular la distancia entre dos puntos usando el Teorema de Pitágoras, y cómo determinar el punto medio de un segmento. También describe cómo calcular el perímetro y área de triángulos y trapecios usando las fórmulas apropiadas. Finalmente, muestra cómo encontrar las coordenadas de un punto de división de un segmento dado la razón de división.

1. Distancia entre 2 puntos y
Punto Medio de un Segmento

2. La distancia d entre dos puntos y se determina mediante
el teorema de Pitágoras así:
1 1 1( , )P x y 2 2 2( , )P x y
1P
2P
1x 2x
1y
2y
0
2 1x x
2 1y y
x
y
d
2 22
2 1 2 1d x x y y
2 2
2 1 2 1d x x y y

3. Calcule el perímetro y el área de cada
polígono de la figura adjunta. A
D C
B
P
R
Q
Y su semiperímetro p es:
El perímetro del triángulo es:ADC 2 5 2 2 2AC CD DA
2 5 2 2 2
1 2 5
2
p
Entonces usando la fórmula del área de un triángulo del matemático griego Herón
de Alejandría (Siglo I DC), se tiene que el área del triángulo ADC esADCA
Ejemplo 5

4. ADCA p p AC p CD p DA
en donde p es el semiperímetro del triángulo ADC, y AC, CD y DA son las medidas
de los lados de dicho triángulo. Entonces:
1 2 5 1 2 5 2 5 1 2 5 2 1 2 5 2 2ADCA
1 2 5 1 2 5 2 5 1 1 5 2
2 2
2 2
2 5 1 1 5 2
6 2 10 2 10 6 2 3 10 10 3 2
Similarmente se obtiene que

5. El perímetro del triángulo ABC es: 2 4 2 2 5
4ABCA
El perímetro del triángulo PQR es: 5 10 17
13
2
PQRA
2 4 2 2 2 2AB BC CD DAEl perímetro del trapecio es:ABCD
ABCDAEl área del trapecio ABCD es: 4 2 6ABCD ABC ADCA A A 
Y su área es:
Y su área es:

6. Considérense dos puntos fijos y y un tercer punto
alineado con ellos y llamado punto de división.
1 1 1( , )P x y 2 2 2( , )P x y ,P x y
1P
2P
1x 2x
1y
2y
0
2x x
2y y
x
y
P
Q
R
x
y
1x x
1 1 1
2 2 2
0
PP x x y y
r
PP x x y y
Por ser semejantes los triángulos
y , se tiene que:1PPQ 2PP R
De donde las coordenadas de P, se
obtienen así:
1 2
1
x rx
x
r
1 2
1
y ry
y
r
La razón se llama razón de semejanza o razón de división del segmento PQ.
1
2
PP
r
PP

7. 1P
2P
1x 2x
1y
2y
0
2x x
2y y
x
y
P
Q
R
x
y
1x x
1 1 1
2 2 2
0
PP x x y y
r
PP x x y y
Por ser semejantes los triángulos
y , se tiene que:1PPQ 2P PR
Un punto P tal que , se llama punto de división interna del segmento
si , y se llama punto de división externa del segmento si .
1
2
PP
r
PP 1 2PP
0r 1 2PP 0r
De donde las coordenadas de P, se
obtienen así:
1 2
1
x rx
x
r
1 2
1
y ry
y
r

8. Ejemplo 6 Determine las coordenadas del punto P de división del
segmento que une al punto con el punto en
la razón .1
3
1,2A 2,1B
Ejemplo 7 Determine las coordenadas del punto P de división del
segmento que une al punto con el punto en
la razón .1
3
1,2A 2,1B
1 7
,
4 4
P
5 5
,
2 2
P