Este documento presenta conceptos básicos de trigonometría como las razones trigonométricas, sus valores en los cuadrantes y para ángulos especiales como los cuadrantales. También define ángulos coterminales y presenta algunos problemas de aplicación.

1. Centro Preuniversitario de la UNS Ingreso Directo
S-04
b
a
H
COSenA 
b
c
H
CA
CosA 
c
a
CA
COTanA 
a
b
CO
HCscA 
c
b
CA
HSecA 
a
c
CO
CA
CotA 
UNIVERSIDAD NACIONAL DEL SANTA
CEPUNS
Ciclo 2016-I
TRIGONOMETRÍA
“R.T. de Ángulos Especiales”
Definición de las Razones Trigonométricas:
*
* α´: se denomina ángulo de referencia
Signos de las R.T. en los cuiadrantes
Dependiendo del cuadrante al que perntenezca un
ángulo en posicionnormal,sus R.T. pueden serpositivas
o negativas. Es asi como se obtiene el cuadro adjunto
Propiedad:
Si  es un ángulo en posición normal positivoy menor
que una vuelta entonces se cumple:
Si   I  0 <  < 90º
Si   II  90º<  <180º
Si   III  180º <  <
270º
Si   IV  270º <  <
360º
Ángulos Cuadrantales
Forma General
< Cuadrantal = 90º.k ; Zk 
También
<Cuadrantal =
2
k ; Zk 
Razones Trigonométricas de Ángulos
Cuadrantales
Nota: N.D. no definido
Ángulos Coterminales:
x
y
P( )x ;y
o o
r
xo
y
o

'
Se define:
o
o
o
o
x
y
Tan
r
x
Cos
r
y
Sen



o
o
o
o
y
r
Csc
x
r
Sec
y
x
Cot



x

Se define:
o
o
o
o
x
y
Tan
r
x
Cos
r
y
Sen



o
o
o
o
y
r
Csc
x
r
Sec
y
x
Cot



2
o
2
o
yxr 
0º 90º 180º 270º 360º
SEN 0 1 0 -1 0
COS 1 0 -1 0 1
TAN 0 ND 0 ND 0
COT ND 0 ND 0 ND
SEC 1 ND -1 ND 1
CSC ND 1 ND -1 ND
Semana Nº
4

2. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
Centro Preuniversitario de la UNS Ingreso Directo
S-04


¡Muy importante!
PROBLEMA DE CLASE
1) El producto de cinco razones
trigonométricas de un ángulo que
pertenece al segundo cuadrante es
dos. Calcular la suma de su seno y
coseno.
a)
5
53 b)
5
5
 c)
2
31 d)
2
13  e)
5
53

2) Del grafico siguiente; hallar tg  + tg

a) 1 b)2 c) 3 d) 2/3 e) 4
EXAMEN PREFERENTE 2012 - I
3) Si  es la medida de un ángulo en
posición normal, además:
0
3
2
cos;0;0   tgtgsensen
Calcular:  SecctgF  .5
A) -1 B) -2 C) -½ D) ½ E) 1
4) Si:
    
 2
2
3
;cos
4
1
2
1
2
1
2


















 senCos
Calcular:   cos16  ctgF
A) 773 B) 767 C) 761
D) 754 E) 727

5) En la figura mostrada si OA = AB,
B(1;7) . Calcular ctg
A) - 4/3 B) - ¾ C) - 1/7 D) -7 E) 25
6) Sean A(-2; -1) , B(4;7) y C(6;-3) los
vértices de un triángulo ABC y K un
punto perteneciente al lado final de una
ángulo en posición normal .Si K Es
circuncentro del triángulo ABC .calcula
11Tg 
A) 4/7 B) 3/4 C) 4/3 D) 2 E) 6
7) De la figura mostrada; calcular:
F = Sec.Csc
Lado
inicial
ii)
P( ; )x x
o o
x
y
Y
X
Q(–b;a)
P(a;b)
R(–a; b)–
M(b;–a)


3. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
Centro Preuniversitario de la UNS Ingreso Directo
S-04
A) – 5/2 B) – 3/2 C) -1 D) ½ E) 3/2
8) De la figura mostrada calcular:


tg
tg
E
9

A) – 49 B) -9 C) 1 D) 9 E) 49
9) De la figura mostrada, calcular:
F= 3sec2
 - tg
A) 7 B) 9 C) 11 D) 13 E) 15
10) Calcular dos ángulos coterminales en
donde el mayor es el séxtuplo del
menor y su suma está comprendido
entre 1000ºy 1050º. Indique el ángulo
mayor.
A) 630º B) 680º C) 700º
D) 800º E) 864º
11) De la figura mostrada si P(a;-b),
calcular el valor de: E = tg.tg
A)-1 B)
2







a
b C)
2






b
a D) 1 E)
2






a
b
12) De la figura mostrada,
simplifique:
)().cos(.
2







 
 CtgsenM
A) sen.2 B) Cos.2 C) sen.
2
2
D) Cos.
2
2 E) Tg.2
13) La expresión :
E = √θ − 2 + √4 − θ
Es real, hallar el valor de:
M = Senθ + Tanθ + Cosθ

4. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
Centro Preuniversitario de la UNS Ingreso Directo
S-04
Cuando ‘‘θ’’ es ángulo cuadrantal
a) 1 b) -1 c) -2 d) 2 e) 3
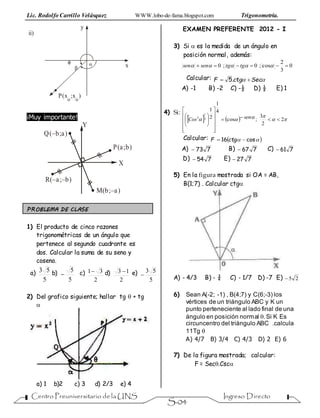
14) Del grafico mostrado, calcular el valor
de:
E = |Cscθ| + Cot|β|
x
y
(2Tanβ; -Secβ)
θ
β
a) √3 b)−√3 c)√3/3
d)−√3/3 e) 1
15) Si: Senθ = −
1
3
−
1
15
−
1
35
− ⋯⏟
´´n´´términos
y Cosθ < 0. Hallar el valor de:
E =
√n + 1
√3n + 1
(Tanθ − Secθ)
a) 0 b) 1 c) -1 d) -1 e) -2
16) Si α ∈ 〈0; π〉 y β ∈ 〈π; 2π〉,
Determine el signo de P, Q y R
P = Csc(β/2)− Cot(1,57 + α/2)
Q = Cos (
β+α
2
) + PCscβ
R = Pcscβ + QCscα
a)(-),(-),(-) b)(-),(+),(+)
c) (+),(+),(+) d)(-),(-),(+)
e)(+),(-),(-)
17) Si θ es un ánguloagudo, hallar todos lo
valores de ‘‘θ’’ para que la expresión:
√2Senθ − 1 + √3 − 5Senθ
Resulte un número real
a) [30°; 53°] b)[30°;90°〉 c) [53°;60°]
d) [37°;90°] e)[30°;37°〉
18) Si: 30° < 𝜃 < 53°. ¿A que es igual?
E = √Sen2
θ − 4Senθ + 4
+ √Sen2
θ − Senθ+
1
4
a) 2Senθ +
5
2
b) 2Senθ−
5
2
c) 3/2
d) 5/2 e) 1/2
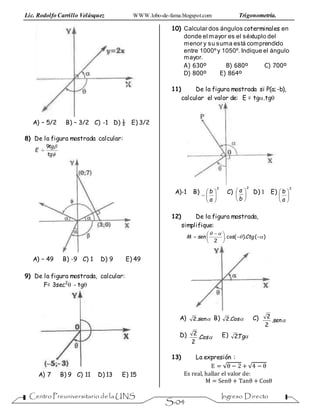
19) De la figura mostrada , MOP es un
sector circular, P=(-3;4) , además
𝐶𝑜𝑠𝛼 + 𝐶𝑜𝑠𝛽 = −1,4 , calcule el area del
rextangulo ABCD
a) 23/4 b) 17/4 c) 21/4 d) 15/4 e) 27/4
20) De la figura mostrada, Calcular 𝑆𝑒𝑐𝛼
a)
√13
2
b) −
√13
2
c) −
√13
3
d)
√13
3
e) √13
21) De la figura mostrada (b>a)
determine 𝑇𝑔𝛼 en terminos a “a” y “b”
a)
𝑎+𝑏
a−b
b)
𝑎−𝑏
a+b
c)
𝑎+𝑏
b−a
d)
𝑏−𝑎
a+b
e)
𝑎+𝑏
2a−b