Este documento presenta el análisis de una torre de agua mediante el uso de ecuaciones cuadráticas y cálculo vectorial. Se midieron y tabularon las dimensiones de los cilindros y otros elementos que componen la torre. Luego, se desarrollaron las ecuaciones cartesianas y paramétricas de cada elemento y se graficaron. Finalmente, se calcularon propiedades como el centro de masa, momentos de inercia y volumen, realizando una comparación con Autocad para validar los resultados.

1. Universidad Politécnica Salesiana. Coronel, Pánchez, Tenezaca, Ortega. Trabajo Integrador C Vectorial
1
IDENTIFICACIÓN, CLASIFICACIÓN Y
ANÁLISIS DE SUPERFICIES CUÁDRICAS Y DE
REVOLUCIÓN EN DIFERENTES
EDIFICIOS Y ELEMENTOS CONSTRUCTIVOS
Coronel Roberto, Pánchez Andrés, Tenezaca Freddy y Ortega Edison
{rcoronelb, ftenezacaq0, apanchez, eortega}@est.ups.edu.ec
Universidad Politécnica Salesiana
Resumen—Este documento presenta el desarrollo y el uso
de conocimientos adquiridos dentro de la materia de cálculo
vectorial para el análisis de estructuras regulares e irregulares,
de manera que podamos obtener de ellos las ecuaciones que
las generan y datos como su centro de masa, momentos de
inercia, volumen, etc.
B. Tabulación de mediciones del sólido
1) La medición de este solido se ha realizado en
una de sus imágenes. Se utilizó el software
“Autocad” (Fig. 1) para la medición de las
dimensiones:
Índice de Términos—Superficies cuadráticas, centro de
masa, momento de inercia.
I. INTRODUCCIÓN
En el transcurso de una carrera de ingeniería y/o
en el área de trabajo encontraremos superficies o
volúmenes de las cuales es necesario saber ciertos
valores, es fácil determinar las ecuaciones mediante
el uso de ecuaciones cuadráticas, para obtener
masas, áreas y volúmenes de un objeto irregular
podemos utilizar las integrales lo cual nos da el
valor con mucha exactitud de lo que necesitamos
saber cómo podremos ver a continuación en la
realización de este trabajo.
II. PROCEDIMIENTO
A. Selección de una obra arquitectónica para
realizar su estudio y construcción
Se seleccionó una edificación, la “Torre Shukov,
siendo esta la primera realización de un
hiperboloide en el año de 1896 por el ingeniero ruso
Vladimir Shukov. Esta torre fue un depósito de agua
que sirvió como modelo a otras 30 estructuras
similares construidas en toda Rusia y a miles,
posteriormente, en el resto del mundo” (No se ha
encontrado mucha información acerca de esta
torre). [1]
Fig. 1: Medicion de las dimenciones en AutoCad

2. Universidad Politécnica Salesiana. Coronel, Pánchez, Tenezaca, Ortega. Trabajo Integrador C Vectorial
2) Tabulación de las medidas. Dimensiones de
cada figura comenzando desde arriba. (Tabla 1)
Figura 1 -- Cilindro (r=1.5)
Radio:
Altura:
Centro de tapa (inf):
Centro de tapa (sup):
Figura 2 -- Cono
Radio (mayor):
Radio (menor):
Altura:
Centro radio (mayor):
Centro radio (menor):
Figura 3 -- Cilindro (r=2.25)
Radio:
Altura:
Centro de tapa (inf):
Centro de tapa (sup):
Figura 4 -- Cilindro (r=5)
Radio:
Altura:
Centro de tapa (inf):
Centro de tapa (sup):
Figura 5 -- Hiperboloide
Radio (inf):
Radio Central Hip:
Radio (sup):
Centro radio (inf):
Centro radio central H:
Centro radio (sup):
1.5m
4m
C(0,0,49)
C(0,0,53)
2.25m
1.5m
3m
C(0,0,46)
C(0,0,49)
2.25m
3m
C(0,0,43)
C(0,0,46)
5m
3m
C(0,0,40)
C(0,0,43)
10m
2.5m
2.7m
C(0,0,0)
C(0,0,34)
C(0,0,40)
Tabla 1: Tabulación de las medidas
3) Figura 3 – Cilindro circular (r=2.25):
4) Figura 4 – Cilindro circular (r=5):
5) Figura 5 – Hiperboloide circular 1h:
D. Ecuaciones Paramétricas:
1) Figura 1 – Cilindro circular(r=1,5):
C:
2) Figura 2 – Cono circular:
C:
C. Ecuaciones cartesianas de las superficies que
conforman el sólido
1) Figura 1 – Cilindro circular(r=1,5):
2) Figura 2 – Cono circular:
3) Figura 3 – Cilindro circular (r=2.25):
C:
2

3. Universidad Politécnica Salesiana. Coronel, Pánchez, Tenezaca, Ortega. Trabajo Integrador C Vectorial
4) Figura 4 – Cilindro circular (r=5):
3) Figura 3 – Cilindro circular (r=2.25):
C:
5) Figura 5 – Hiperboloide circular 1h:
4) Figura 4 – Cilindro circular (r=5):
C:
E. Gráfica de las superficies parametrizadas en
el Winplot. (Fig. 2)
1) Figura 1 – Cilindro circular(r=1,5):
5) Figura 5 – Hiperboloide circular 1h:
2) Figura 2 – Cono circular:
3

4. Universidad Politécnica Salesiana. Coronel, Pánchez, Tenezaca, Ortega. Trabajo Integrador C Vectorial
Fig. 2: Grafica de la estructura en Winplot.
F. Centro de Masa y Momentos de Inercia
A continuación se presenta cada una los valores de
cada elemento que conforma el sólido (Tabla 2).
Los respectivos cálculos se anexaran al final con
formato “Derive”.
Figura 1 -- Cilindro (r=1.5)
Masa (= Volúmen)
Momento YZ:
Momento XZ:
Momento XY:
Centro de masa:
Momento de inercia X:
Momento de inercia Y:
Momento de inercia Z:
Figura 2 -- Cono
Masa (= Volúmen)
Momento YZ:
28,274
0,000
0,000
1441,991
(0,0,51)
73595,146
73595,146
31,809
33,578
0,000
Momento XZ:
Momento XY:
Centro de masa:
Momento de inercia X:
Momento de inercia Y:
Momento de inercia Z:
Figura 3 -- Cilindro (r=2.25)
Masa (= Volúmen)
Momento YZ:
Momento XZ:
Momento XY:
Centro de masa:
Momento de inercia X:
Momento de inercia Y:
Momento de inercia Z:
Figura 4 -- Cilindro (r=5)
Masa (= Volúmen)
Momento YZ:
Momento XZ:
Momento XY:
Centro de masa:
Momento de inercia X:
Momento de inercia Y:
Momento de inercia Z:
Figura 5 -- Hiperboloide
Masa (= Volúmen)
Momento YZ:
Momento XZ:
Momento XY:
Centro de masa:
Momento de inercia X:
Momento de inercia Y:
Momento de inercia Z:
Figura Total
Masa (= Volúmen)
Momento YZ:
Momento XZ:
Momento XY:
Centro de masa:
Momento de inercia X:
Momento de inercia Y:
Momento de inercia Z:
4
0,000
1588,222
(0,0,47.3)
75172,773
75172,773
62,921
47,713
0,000
0,000
2123,226
(0,0,44.5)
94579,718
94579,718
120,773
235,619
0,000
0,000
9778,207
(0,0,41.5)
73595,146
73595,146
2945,243
3270,381
0,000
0,000
33516,298
(0,0,10.25)
682104,398
682104,398
81854,984
3615,563
0,000
0,000
33516,298
(0,0,13.3998)
1332896,966
1332896,966
85015,731
Tabla 2: Centros de Masa y Momentos de Inercia

5. Universidad Politécnica Salesiana. Coronel, Pánchez, Tenezaca, Ortega. Trabajo Integrador C Vectorial
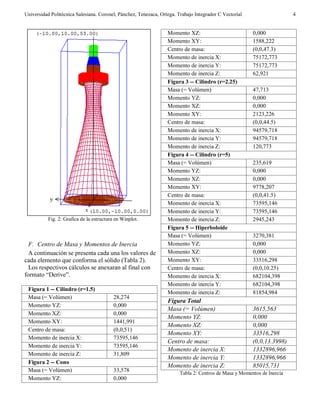
III. ANÁLISIS DE RESULTADOS
Para poder hacer una comparación y sacar los
errores, diseñamos la figura el AutoCad 3D (Fig. 3),
donde una opción nos permite visualizar las
propiedades de la figura. (Fig. 4).
5
IV. CUADRO DE ERRORES
Valores
AutoCad
Calculados
% Error
Volúmen:
3615,563
3615,563
0,00000
Momento YZ:
0,000
0,000
0,00000
Momento XZ:
0,000
0,000
0,00000
Momento XY:
33516,298
Centro masa(z):
(0,0,13.3999)
(0,0,13.3998)
7.46E-4
MI X:
1332906,890
1332896,966
0.003
MI Y:
1332906,890
1332896,966
0.003
MI Z:
85015,730
85015,731
-1.17E-6
V. OBSERVACIONES
Al ver la tabla de errores entre los datos obtenidos
en Autocad con los datos calculados, podemos
darnos cuenta que el porcentaje de error es mínimo.
VI. CONCLUSIONES
Fig. 3: Diseño de la figura en 3D.
El uso de integrales en figuras irregulares para
obtener valores de área, volúmen, centro de masa,
etc., no permite obtener una respuesta igual a la real
a diferencia de la sumatoria de Rieman (cuando i,
m, n no tienden al infinito) que solo nos da un valor
aproximado del que esperamos.
Los conocimientos adquiridos en la materia de
cálculo vectorial son adecuados para conseguir lo
desarrollado en este documento.
Las ecuaciones paramétricas a diferencia de las
ecuaciones rectangulares, nos permiten generar la
figura deseada con los límites que son requeridos.
REFERENCIAS
[1] http://blog.ql-ingenieria.es/2012/vladimir-shukov/.
VII. ANEXOS:
Archivo con el desarrollo de las ecuaciones realizado en
Derive. Formato Derive.
Fig 4: Propiedades del solido.