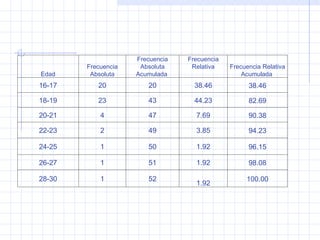
El documento presenta diferentes tipos de gráficos y representaciones para variables cualitativas y cuantitativas. Explica diagramas circulares, de barras y sectores para variables cualitativas, así como histogramas, diagramas de barras y cajas para variables cuantitativas discretas y continuas. También describe diagramas integrales y de dispersión.

1. REPRESENTACIÓN GRÁFICA DE DATOS

2. Gráficos para v ariables cualitativas o categ óricas Estas son algunas de las representaciones más utilizadas para variables categóricas. Diagrama circular Gráfico de barras

3. Diagramas de barras Alturas proporcionales a las frecuencias abs olutas o rel ativas. Se pueden aplicar también a variables discretas Diagramas de sectores (tartas, polares) El área de cada sector es proporcional a su frecuencia abs oluta o rel ativa . Pictogramas Fáciles de entender.

4. Las variables cuantitativas continúas toman un número considerable de valores. Su representación gráfica resulta más clara si se agrupan los valores próximos de la variable. El gráfico más común de la distribución de una variable cuantitativa continúa es un histograma . Gráficos para variables cuantitativas

5. Gráficos diferenciales para variables numéricas Son diferentes en función de que las variables sean discretas o continuas . Se hac en con frec uencias absolutas o relativas. Diagramas barras para v. discretas Se deja un hueco entre barras para indicar los valores que no son posibles Histogramas para v. continuas El área que hay bajo el histograma entre dos puntos cualesquiera indica la cantidad (porcentaje o frecuencia) de individuos en el intervalo.

6. El Histograma consiste en una serie de rectángulos, cuya base son los intervalos de clase y su altura la densidad correspondiente (frecuencia). La suma de las áreas debe dar 100% ó 1.00.

8. Diagramas integrales

9. Diagramas integrales

10. La ojiva Representa un segmento de la recta, cuya pendiente es la densidad del intervalo respectivo.

11. Gráfico de Cajas Mínimo Máximo Mediana 1er cuartil 3er cuartil

12. Gráficos de dispersión

13. DESCRIPCIÓN: Es un gráfico de barras que presenta en forma ordenada el grado de importancia de problemas o factores de un problema y por tanto ayuda a determinar prioridades. DIAGRAMA DE PARETO Italiano Wilfredo Pareto: Los problemas se deben a pocas causas vitales y no a las muchas triviales.

14. Población FUENTE: ESTUDIO DE RECURSOS HUMANOS, INVESTIGACION NAC. MORBILIDAD – MIN. SALUD – ASCOFAME – COLOMBIA 1966 Muestra Conjunto de elementos que tiene al menos una caracterisca suceptible de ser medida o estudiada. Población Finita Población Infinita La muestra es un subconjunto Muestreo : Procedimiento estadístico mediante el cual es posible conocer las características de una población.

15. ESTRATEGIA EDUCATIVA MODIFICA HABITOS VALIDEZ INTERNA “ todos son elegibles para participar” n VALIDEZ EXTERNA POBLACIÓN FUENTE MARCO MUESTRAL muestra POBLACIÓN OBJETIVO PERSONAS CON ESTE TIPO DE PROBLEMAS CRITERIOS DE INCLUSION N “ Debe ser PROBABILISTICA” TRABAJADORES DE UNA EMPRESA

16. TIPOS DE MUESTRAS Probabilísticas No probabilísticas Aleatoria Sistemática Estratificada Por conglomerados Conveniencia Cuotas Bola de nieve

17. VARIABLE INDEPENDIENTE Es aquella cuyo valor en un estudio no está influida por la enfermedad o efecto analizado. Pero puede causarlos o contribuir a su variación.

18. VARIABLE DEPENDIENTE Es aquella cuyo valor en un estudio depende del efecto que sobre ella causen otras variables. Para describir los valores que toma se utiliza: escalas de medición y niveles de medición

19. CLASE 2 TABLAS DE FRECUENCIA

20. ¿Para qué se construyen las tablas de frecuencias ? ORDENAR AGRUPAR RESUMIR información

21. Exponen la información recogida en la muestra, de forma que no se pierda nada de información (o poca). Frecuencias absolutas : Contabilizan el número de individuos de cada modalidad Frecuencias relativas : Contabilizan el número de individuos de cada modalidad, pero dividido por el total , por lo tanto presentan es un porcentaje Frecuencias acumuladas : Sólo tienen sentido para variables ordinales y numéricas . Muy útiles para calcular cuartiles (ver más adelante) Tablas de frecuencia

22. Tablas de frecuencia Género Frecuencia Absoluta Frec uencia relat iva % Hombre 4 4/10 *100 =40% Mujer 6 6/10 *100 =60% 10 Tamaño muestral

23. Frecuencias absolutas Se usan para conocer la magnitud de algunos problemas o ciertas características de la población estudiada, pero revelan poco sobre el riesgo de una población, o la probabilidad de enfermar de la misma población. Ejemplo: # de muertes o enfermedades

24. Frecuencias relativas Señalan con mayor precisión la magnitud de un problema y en ocasiones permiten conocer con cierta exactitud el grado de riesgo que tiene una población de sufrir un determinado daño a la salud.

25. EJEMPLO En una clase de 30 alumnos se ha preguntado el número de hermanos que tienen, el resultado ha sido el siguiente: 1 1 0 1 2 1 5 3 6 2 0 3 0 1 1 2 3 4 4 2 1 1 1 2 0 3 1 1

26. Si presentamos esta información en una tabla de frecuencias , queda como sigue: Total 30 N ° de hermanos Frecuencia Absoluta Frecuencia Relativa 0 1 2 3 4 5 6 4 12 6 4 2 1 1

27. Estatura de los alumnos de la clase de natación Datos Alumno Estatura Alumno Estatura Alumno Estatura Alumno 1 125 Alumno 11 123 Alumno 21 121 Alumno 2 128 Alumno 12 126 Alumno 22 129 Alumno 3 127 Alumno 13 130 Alumno 23 126 Alumno 4 121 Alumno 14 121 Alumno 24 122 Alumno 5 122 Alumno 15 128 Alumno 25 128 Alumno 6 129 Alumno 16 130 Alumno 26 127 Alumno 7 130 Alumno 17 122 Alumno 27 126 Alumno 8 124 Alumno 18 125 Alumno 28 123 Alumno 9 127 Alumno 19 120 Alumno 29 122 Alumno 10 129 Alumno 20 128 Alumno 30 121

28. Tabla de frecuencia Variable Frecuencias absolutas Frecuencias relativas Talla en cm Simple Acumulada Simple Acumulada 120 1 1 3,3% 3,3% 121 4 5 13,3% 16,6% 122 4 9 13,3% 30,0% 123 2 11 6,6% 36,6% 124 1 12 3,3% 40,0% 125 2 14 6,6% 46,6% 126 3 17 10,0% 56,6% 127 3 20 10,0% 66,6% 128 4 24 13,3% 80,0% 129 3 27 10,0% 90,0% 130 3 30 10,0% 100,0%

29. PRINCIPALES CAUSAS DE ACCIDENTALIDAD EN LA EMPRESA XYZ. Teniendo en cuenta la siguiente tabla de datos recolectados durante el 2010. Parte del Grupo Horario Cuerpo Mañana Tarde Noche Tórax A 1 1 1 B - - 1 C 1 1 2 D 1 2 - Manos A 3 3 4 B 3 2 6 C 3 3 5 D 2 2 5 Ojos A 1 1 2 B - 1 1 C 2 1 1 D 1 2 1 Piernas A 1 2 2 B 2 3 2 C 1 2 1 D 2 1 1

30. ACCIDENTES POR PARTE DEL CUERPO LESIONADA Parte del Frecuencia Frec. Abs. Frecuencia Frec. Relativa Cuerpo Absoluta acumulada Relativa % Acumulada Manos 41 41 47.7 47.7 Piernas 20 61 23.2 70.9 Ojos 14 75 16.3 87.2 Tórax 11 86 12.8 100.0 Total 86 - 100.0

31. CONCLUSIONES : Teniendo en cuenta la estratificación en diferentes grupos y los diagramas de pareto realizados se puede concluir que : La parte del cuerpo mas afectada en los accidentes de trabajo en la empresa el último mes son las manos con un 47.7% de lesiones. El horario en que ocurren la mayoría de los accidentes en la empresa es en la noche, con un 40.7 % de accidentes. El 57% de los accidentes ocurren en la noche y se han lesionado las manos. El grupo B presenta el 30% de las lesiones en las manos y en la noche, mientras que el grupo A presenta el 20% de las lesiones en las manos y en la noche.

32. Si los valores que toma la variable son muy diversos y cada uno de ellos se repite muy pocas veces, entonces conviene agruparlos por intervalos, a estos intervalos se les denomina clase y se pueden obtener a partir de la siguiente formula: K= 1+ 3.32*log n donde n es el tamaño de la muestra K indica cuantos intervalos La amplitud del intervalo se calcula dividiendo el rango entre esta constante A = R K Recordemos que rango es la diferencia entre el valor mayor y el valor menor Tablas de frecuencia

33. Se presenta en la tabla la edad en años de los estudiantes de primer semestre de salud ocupacional organizar los datos en una tabla de frecuencia. K = 1 + 3,32. log52 = 6.7 R = 30 – 16 = 14 A = 14/6.7 = 2.0 # Edad # Edad 1 19 27 18 2 30 28 19 3 17 29 17 4 21 30 20 5 16 31 19 6 19 32 19 7 19 33 17 8 17 34 22 9 17 35 17 10 17 36 18 11 17 37 18 12 17 38 16 13 19 39 18 14 16 40 18 15 16 41 19 16 16 42 16 17 20 43 18 18 22 44 18 19 16 45 18 20 18 46 19 21 25 47 16 22 20 48 18 23 19 49 17 24 16 50 19 25 18 51 17 26 27 52 19

34. Edad Frecuencia Absoluta Frecuencia Absoluta Acumulada Frecuencia Relativa Frecuencia Relativa Acumulada 16-17 20 20 38.46 38.46 18-19 23 43 44.23 82.69 20-21 4 47 7.69 90.38 22-23 2 49 3.85 94.23 24-25 1 50 1.92 96.15 26-27 1 51 1.92 98.08 28-30 1 52 1.92 100.00

35. VARIABLE PESO Kilos 50 – 42 – 55 – 60 – 46 47 – 62 – 71 – 48 – 59 83 – 90 – 66 – 71 – 85 52 – 45 – 59 – 74 – 81-57 - 50

36. Ejercicio Organizar en una tabla de frecuencia los siguientes datos: Peso Frec. absoluta Frec. Abs. acumulada Frec. relativa F. Relativa acumulada

37. Que porcentaje de individuos tiene entre 78 y 86 kg.? Que porcentaje de individuos tiene menos de 78 Kg? Peso Frec. absoluta Frec. Abs. acumulada Frec. Relativa F. Relativa acumulada 42 - 50 7 7 31.8 31.8 51 – 59 5 12 22.72 54.52 60 - 68 3 15 13.63 68.15 69 - 77 3 18 13.63 81.78 78 - 86 3 21 13.63 95.41 87 - 90 1 22 4.54 99.95

38. EJEMPLO Se toma la información sobre el número de pacientes que llegan a un hospital el fin de semana de las 2 a.m a las 6 a.m., observando una muestra de 25 fines de semana, se obtuvieron los siguientes resultados: 8, 3, 7, 9, 8, 7, 8, 10, 4, 10, 12, 7, 9, 8, 7, 6, 5, 10, 7, 4, 5, 6, 11, 10, 15. Construir la tabla de frecuencias, además de su distribución. Representar gráficamente la información.

39. GRACIAS