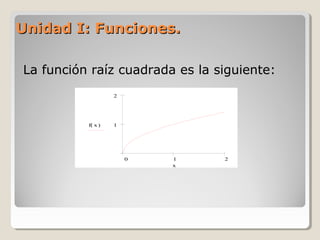
Este documento presenta información sobre funciones matemáticas. Explica conceptos como relaciones, funciones, dominio y rango. Describe funciones específicas como lineales, cuadráticas, exponenciales y logarítmicas. También cubre temas como gráficas de funciones, composición de funciones, y funciones pares e impares.