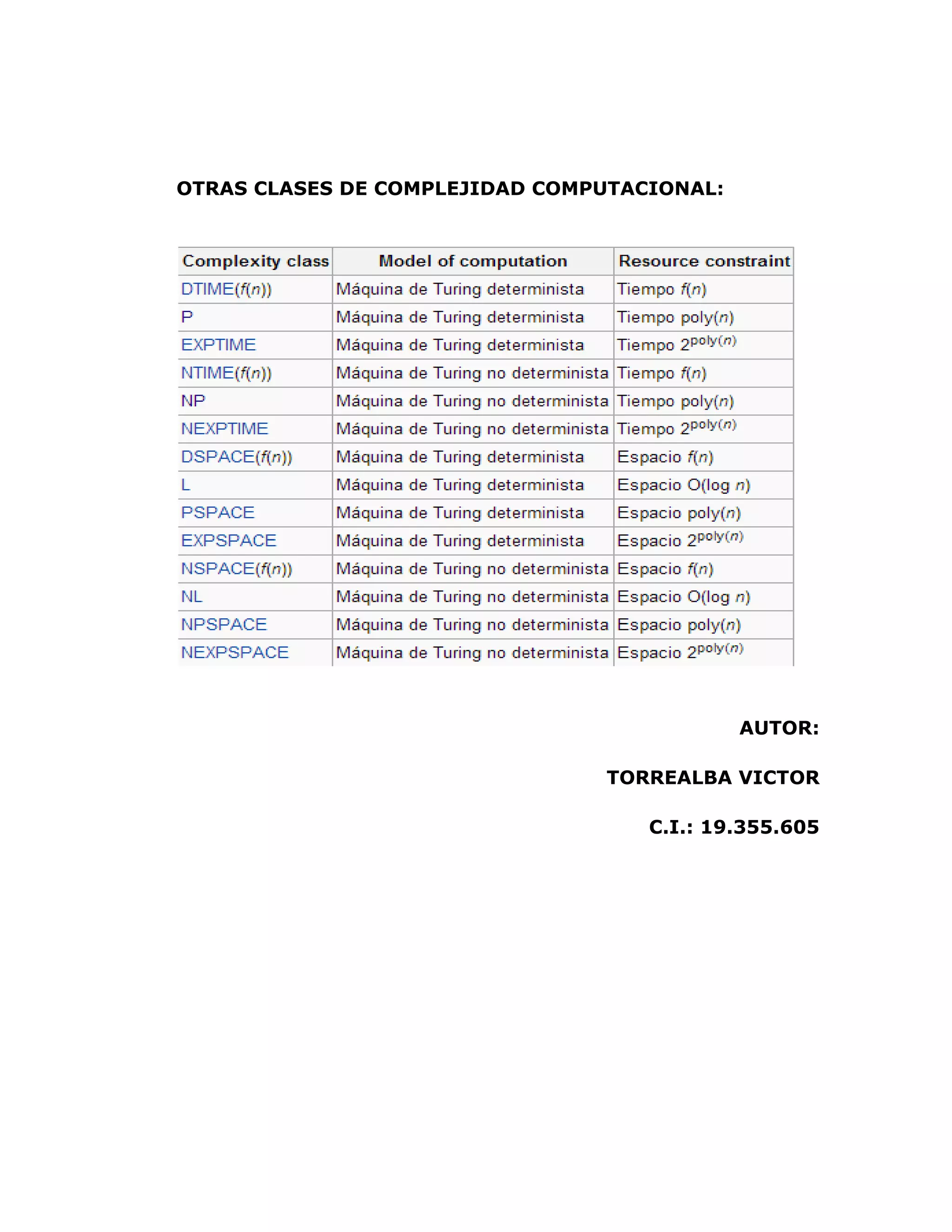
Las clases de complejidad computacional se definen considerando factores como el tipo de problema, el modelo de cómputo y los recursos acotados. La clase P contiene problemas solubles en tiempo polinómico por una máquina de Turing determinista. La clase NP incluye problemas de decisión para los cuales existe un certificado verificable en tiempo polinómico. El problema de satisfacibilidad booleana fue el primero en demostrarse NP-completo, lo que significa que es el problema más difícil en esta clase.

1. CLASES DE COMPLEJIDAD COMPUTACIONAL
DEFINICIÓN DE CLASES DE COMPLEJIDAD
COMPUTACIONAL:
Las clases de complejidad más sencillas se definen teniendo
en cuenta factores como:
 El tipo de problema computacional: Los problemas más
comúnmente utilizados son los problemas de decisión, pero
las clases de complejidad se pueden definir para otros tipos
de problemas.
 El modelo de cómputo: El modelo de cómputo más común es
la Máquina de Turing determinista, pero muchas clases de
complejidad se basan en Máquinas de Turing no
deterministas, Máquinas de Turing cuánticas, etc.
 El recurso (o recursos) que está(n) siendo acotado(s) y la(s)
cota(s): Estas dos propiedades usualmente se utilizan juntas,
por ejemplo, "tiempo polinomial", "espacio logarítmico",
"profundidad constante", etc.
CLASE P:
La clase P contiene a aquellos problemas que son solubles en
tiempo polinómico por una máquina de Turing determinista.5
Para la definición anterior se ha fijado el modelo de cómputo:
la Máquina de Turing determinista. Existen distintas variantes de la

2. Máquina de Turing y es conocido que la más débil de ellas puede
simular a la más fuerte, adicionando a lo sumo un tiempo
polinómico. En las décadas posteriores a la Tesis de Church-
Turing surgieron otros modelos de cómputo, y se pudo mostrar que
la Máquina de Turing también podía simularlos a lo sumo
adicionando también un tiempo polinómico. Por tanto, la clase
análoga a P para dichos modelos no es mayor que la clase P para el
modelo de cómputo de la máquina de Turing.
La clase P juega un papel importante en la teoría de la
complejidad computacional debido a que:
1. P es invariante para todos los modelos de cómputo que son
polinómicamente equivalentes a la Máquina de Turing
determinista.
2. A grandes rasgos, P corresponde a la clase de problemas que,
de manera realista, son solubles en una computadora.
CLASE NP:
La importancia de esta clase de problemas de decisión es que
contiene muchos problemas de búsqueda y de optimización para los
que se desea saber si existe una cierta solución o si existe una
mejor solución que las conocidas. En esta clase están el problema
del viajante (también llamado "problema del viajante de
comercio" o "problema del agente viajero") donde se quiere saber
si existe una ruta óptima que pasa por todos los nodos en un
cierto grafo y el problema de satisfacibilidad booleana en donde se

3. desea saber si una cierta fórmula de lógica proposicional puede ser
cierta para algún conjunto de valores booleanos para las variables.
Dada su importancia, se han hecho muchos esfuerzos para
encontrar algoritmos que decidan algún problema de NP en tiempo
polinómico. Sin embargo, pareciera que para algunos problemas de
NP (los del conjunto NP-completo) no es posible encontrar un
algoritmo mejor que simplemente realizar una búsqueda
exhaustiva.
En el artículo de 2002, "PRIMES is in P", Manindra Agrawal
con sus estudiantes1 ,2
encontró un algoritmo que trabaja en tiempo
polinómico para el problema de saber si un número es primo.
Anteriormente se sabía que ese problema estaba en NP, si bien no
en NP-completo, ahora se sabe que también está en P.
El primer problema natural que se demostró que es completo
NP fue el problema de satisfacibilidad booleana. Este resultado fue
demostrado por Stephen Cook en 1971, y se lo llamó el teorema de
Cook. La demostración de Cook de que la satisfacibilidad es un
problema NP-completo es muy complicada. Sin embargo, después
de que este problema se demostrara que es NP-Completo, es fácil
demostrar que muchos otros problemas pertenecen a esta clase.
Por lo tanto, una amplia clase de problemas en principio inconexos
son reducibles unos a otros, y por lo tanto resultan en "el mismo
problema" -- un resultado profundo e inesperado.

4. OTRAS CLASES DE COMPLEJIDAD COMPUTACIONAL:
AUTOR:
TORREALBA VICTOR
C.I.: 19.355.605