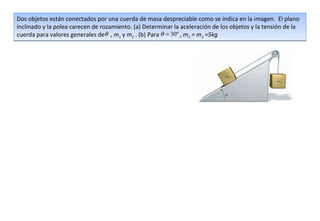
Este documento describe cómo determinar la aceleración y tensión de la cuerda para dos objetos conectados por una cuerda sobre un plano inclinado sin rozamiento. Se dibujan diagramas de fuerzas para cada objeto y se aplica la segunda ley de Newton para obtener expresiones para la aceleración y tensión en términos de las masas y el ángulo de inclinación. Luego se sustituyen valores numéricos para obtener los resultados específicos.

1. Dos objetos están conectados por una cuerda de masa despreciable como se indica en la imagen. El plano
inclinado y la polea carecen de rozamiento. (a) Determinar la aceleración de los objetos y la tensión de la
cuerda para valores generales deθ , m1 y m2 . (b) Para θ = 30º , m1 = m2 =5kg

2. Dos objetos están conectados por una cuerda de masa despreciable como se indica en la imagen. El plano
inclinado y la polea carecen de rozamiento. (a) Determinar la aceleración de los objetos y la tensión de la
cuerda para valores generales deθ , m1 y m2 . (b) Para θ = 30º , m1 = m2 =5kg
(a) Dibujamos un diagrama de fuerzas para el bloque m1 en el
que se reflejen todas las fuerzas que actúan sobre él:

3. Dos objetos están conectados por una cuerda de masa despreciable como se indica en la imagen. El plano
inclinado y la polea carecen de rozamiento. (a) Determinar la aceleración de los objetos y la tensión de la
cuerda para valores generales deθ , m1 y m2 . (b) Para θ = 30º , m1 = m2 =5kg
(a) Dibujamos un diagrama de fuerzas para el bloque m1 en el
que se reflejen todas las fuerzas que actúan sobre él:
El eje x coincide con la dirección del plano
inclinado.

4. Dos objetos están conectados por una cuerda de masa despreciable como se indica en la imagen. El plano
inclinado y la polea carecen de rozamiento. (a) Determinar la aceleración de los objetos y la tensión de la
cuerda para valores generales deθ , m1 y m2 . (b) Para θ = 30º , m1 = m2 =5kg
(a) Dibujamos un diagrama de fuerzas para el bloque m1 en el
que se reflejen todas las fuerzas que actúan sobre él:
El eje x coincide con la dirección del plano
inclinado.
 
Aplicando ∑ F = ma , obtenemos
T − m1 g sin θ = m1a

5. Dos objetos están conectados por una cuerda de masa despreciable como se indica en la imagen. El plano
inclinado y la polea carecen de rozamiento. (a) Determinar la aceleración de los objetos y la tensión de la
cuerda para valores generales deθ , m1 y m2 . (b) Para θ = 30º , m1 = m2 =5kg
(a) Dibujamos un diagrama de fuerzas para el bloque m1 en el
que se reflejen todas las fuerzas que actúan sobre él:
El eje x coincide con la dirección del plano
inclinado.
 
Aplicando ∑ F = ma , obtenemos
T − m1 g sin θ = m1a
Dibujamos otro diagrama para el segundo cuerpo, y aplicamos de nuevo la segunda ley de Newton para
obtener:

6. Dos objetos están conectados por una cuerda de masa despreciable como se indica en la imagen. El plano
inclinado y la polea carecen de rozamiento. (a) Determinar la aceleración de los objetos y la tensión de la
cuerda para valores generales deθ , m1 y m2 . (b) Para θ = 30º , m1 = m2 =5kg
(a) Dibujamos un diagrama de fuerzas para el bloque m1 en el
que se reflejen todas las fuerzas que actúan sobre él:
El eje x coincide con la dirección del plano
inclinado.
 
Aplicando ∑ F = ma , obtenemos
T − m1 g sin θ = m1a
Dibujamos otro diagrama para el segundo cuerpo, y aplicamos de nuevo la segunda ley de Newton para
obtener:
m2 g − T = m2 a

7. Dos objetos están conectados por una cuerda de masa despreciable como se indica en la imagen. El plano
inclinado y la polea carecen de rozamiento. (a) Determinar la aceleración de los objetos y la tensión de la
cuerda para valores generales deθ , m1 y m2 . (b) Para θ = 30º , m1 = m2 =5kg
(a) Dibujamos un diagrama de fuerzas para el bloque m1 en el
que se reflejen todas las fuerzas que actúan sobre él:
El eje x coincide con la dirección del plano
inclinado.
 
Aplicando ∑ F = ma , obtenemos
T − m1 g sin θ = m1a
Dibujamos otro diagrama para el segundo cuerpo, y aplicamos de nuevo la segunda ley de Newton para
obtener:
m2 g − T = m2 a
Sumamos las dos ecuaciones y despejamos la aceleración:
g (m2 − m1 sin θ )
a=
m1 + m2

8. Dos objetos están conectados por una cuerda de masa despreciable como se indica en la imagen. El plano
inclinado y la polea carecen de rozamiento. (a) Determinar la aceleración de los objetos y la tensión de la
cuerda para valores generales deθ , m1 y m2 . (b) Para θ = 30º , m1 = m2 =5kg
Basta ahora con sustituir la expresión obtenida para la
aceleración en una de las ecuaciones que contienen
la tensión y despejar la misma:

9. Dos objetos están conectados por una cuerda de masa despreciable como se indica en la imagen. El plano
inclinado y la polea carecen de rozamiento. (a) Determinar la aceleración de los objetos y la tensión de la
cuerda para valores generales deθ , m1 y m2 . (b) Para θ = 30º , m1 = m2 =5kg
Basta ahora con sustituir la expresión obtenida para la
aceleración en una de las ecuaciones que contienen
la tensión y despejar la misma:
g (m2 − m1 sin θ )
a=
m1 + m2
T − m1 g sin θ = m1a

10. Dos objetos están conectados por una cuerda de masa despreciable como se indica en la imagen. El plano
inclinado y la polea carecen de rozamiento. (a) Determinar la aceleración de los objetos y la tensión de la
cuerda para valores generales deθ , m1 y m2 . (b) Para θ = 30º , m1 = m2 =5kg
Basta ahora con sustituir la expresión obtenida para la
aceleración en una de las ecuaciones que contienen
la tensión y despejar la misma:
g (m2 − m1 sin θ )
a= gm1m2 (1 + sin θ )
m1 + m2 ⇒ T=
m1 + m2
T − m1 g sin θ = m1a

11. Dos objetos están conectados por una cuerda de masa despreciable como se indica en la imagen. El plano
inclinado y la polea carecen de rozamiento. (a) Determinar la aceleración de los objetos y la tensión de la
cuerda para valores generales deθ , m1 y m2 . (b) Para θ = 30º , m1 = m2 =5kg
Basta ahora con sustituir la expresión obtenida para la
aceleración en una de las ecuaciones que contienen
la tensión y despejar la misma:
g (m2 − m1 sin θ )
a= gm1m2 (1 + sin θ )
m1 + m2 ⇒ T=
m1 + m2
T − m1 g sin θ = m1a
(b) Sustituimos los valores numéricos en las expresiones de la aceleración y la tensión, y obtenemos:
a = 2.45 m s 2, T = 36.8 N