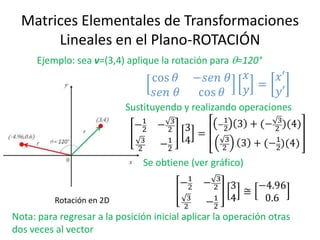
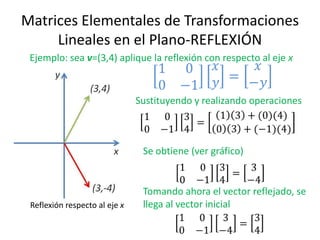
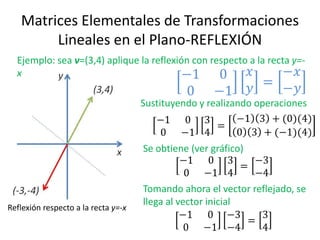
El documento presenta una introducción a las transformaciones lineales, específicamente reflexiones y rotaciones en el plano R2, ilustrando cómo estas se representan mediante matrices. Se incluyen ejemplos prácticos de reflexiones respecto a los ejes y rectas, así como rotaciones en 2D, mostrando el proceso de mapeo de vectores. Además, se citan referencias relevantes para profundizar en el tema.

1. Transformaciones Lineales
-Reflexión y Rotación en R2-
Representación Matricial
José Luis Morales
Universidad de América Latina
UDAL

2. Introducción a las
Transformaciones Lineales
• Son funciones que transforman (o mapean) un
espacio vectorial V en un espacio vectorial W. este
tipo de función se denota por: T:VW.

3. 5
REFLEXION
Castillo de Urquhart.
El Lago Ness, Escocia [1]

4. Matrices Elementales de Transformaciones
Lineales en el Plano-REFLEXIÓN
• Reflexión respecto al eje x• Reflexión respecto al eje y
y
x
(x,y)(-x,y)
y
x
(x,y)
(x,-y)

5. Matrices Elementales de Transformaciones
Lineales en el Plano-REFLEXIÓN
Reflexión respecto al eje y
Ejemplo: sea v=(3,4) aplique la reflexión con respecto al eje y
Sustituyendo y realizando operaciones
Se obtiene (ver gráfico)
Tomando ahora el vector reflejado, se
llega al vector inicial

6. Matrices Elementales de Transformaciones
Lineales en el Plano-REFLEXIÓN
Ejemplo: sea v=(3,4) aplique la reflexión con respecto al eje x
Sustituyendo y realizando operaciones
Se obtiene (ver gráfico)
Tomando ahora el vector reflejado, se
llega al vector inicialReflexión respecto al eje x

7. Matrices Elementales de Transformaciones
Lineales en el Plano-REFLEXIÓN
Ejemplo: sea v=(3,4) aplique la reflexión con respecto a la recta y=-
x
Sustituyendo y realizando operaciones
Se obtiene (ver gráfico)
Tomando ahora el vector reflejado, se
llega al vector inicial
Reflexión respecto a la recta y=-x

8. Matrices Elementales de Transformaciones
Lineales en el Plano-REFLEXIÓN
Ejemplo: sea v=(3,4) aplique la reflexión con respecto a la recta y=x
Sustituyendo y realizando operaciones
Se obtiene (ver gráfico)
Tomando ahora el vector reflejado, se
llega al vector inicial
Reflexión respecto a la recta y=x

9. ROTACION
Autor: Escher [2]

10. Matrices Elementales de Transformaciones
Lineales en el Plano-ROTACIÓN
Rotación en 2D
Ejemplo: sea v=(3,4) aplique la rotación para =120°
Sustituyendo y realizando operaciones
Se obtiene (ver gráfico)
Nota: para regresar a la posición inicial aplicar la operación otras
dos veces al vector

11. Referencias
• Grossman, S.L. (2011). Matemáticas 4, Álgebra Lineal.
México, D.F.: McGraw-Hill
• Lay, D.C. (2006). Linear Algebra and its applications.
United States of America. Pearson Addison Wesley
• Poole, D. (2011). Álgebra Lineal, Una introducción
moderna. México, D.F.: Cengage Learning
• Williams, G. (2008). Linear Algebra with applications.
United States of America. Jones and Bartlett Publishers
• 1. Imagen tomada de la página www.sobreturismo.es
• 2. Imagen tomada de www.marvin.com.mx