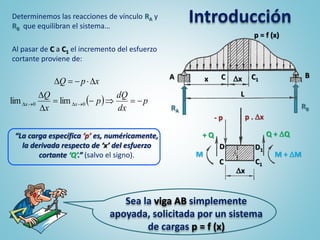
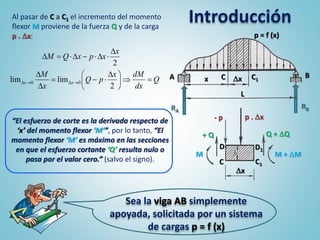
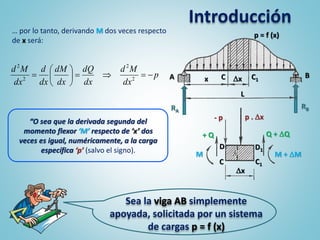
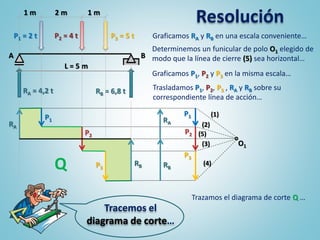
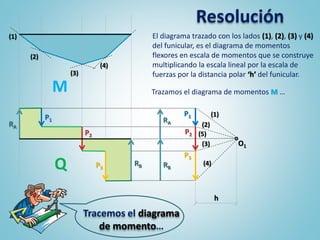
El documento presenta los pasos para determinar gráficamente los diagramas de características de una viga simplemente apoyada sometida a cargas. Primero se grafican las cargas y reacciones de apoyo, luego se traza el diagrama de corte y finalmente el diagrama de momentos flexores. Estos diagramas permiten visualizar la distribución de esfuerzos a lo largo de la viga y son una herramienta útil para el análisis de vigas.

1. Diagrama de
Características
Determinación Gráfica
Curso de Estabilidad IIb
Ing. Gabriel Pujol
Para las carreas de Ingeniería Mecánica e Ingeniería Naval y Mecánica de la
Facultad de Ingeniería de la Universidad de Buenos Aires

2. Sea la viga AB simplemente
apoyada, solicitada por un sistema
de cargas p = f (x)
Determinemos las reacciones de vínculo RA y
RB que equilibran el sistema…
Introducción
RA
RB
p = f (x)
A BC C1x x
L
Al pasar de C a C1 el incremento del esfuerzo
cortante proviene de:
  p
dx
dQ
p
x
Q
xpQ
xx 



 00 limlim
“La carga específica ‘p’ es, numéricamente,
la derivada respecto de ‘x’ del esfuerzo
cortante ‘Q’.” (salvo el signo).
p . x- p
+ Q Q + Q
x
C C1
D1D
M M + M

3. Sea la viga AB simplemente
apoyada, solicitada por un sistema
de cargas p = f (x)
Introducción
RA
RB
p = f (x)
A BC C1x x
L
Al pasar de C a C1 el incremento del momento
flexor M proviene de la fuerza Q y de la carga
p . x:
“El esfuerzo de corte es la derivada respecto de
‘x’ del momento flexor ‘M’”, por lo tanto, “El
momento flexor ‘M’ es máximo en las secciones
en que el esfuerzo cortante ‘Q’ resulta nulo o
pasa por el valor cero.” (salvo el signo).
p . x- p
+ Q Q + Q
x
C C1
D1D
M M + M
Q
dx
dMx
pQ
x
M
x
xpxQM
xx 




 






2
limlim
2
00

4. Sea la viga AB simplemente
apoyada, solicitada por un sistema
de cargas p = f (x)
Introducción
RA
RB
p = f (x)
A BC C1x x
L
… por lo tanto, derivando M dos veces respecto
de x será:
“O sea que la derivada segunda del
momento flexor ‘M’ respecto de ‘x’ dos
veces es igual, numéricamente, a la carga
específica ‘p’ (salvo el signo).
p . x- p
+ Q Q + Q
x
C C1
D1D
M M + M
p
dx
Md
dx
dQ
dx
dM
dx
d
dx
Md






 2
2
2
2

5. Determinemos gráficamente los
diagramas de características de la
siguiente viga...
Enunciado
RA = 4,2 t RB = 6,8 t
Sea la viga AB simplemente apoyada, solicitada
por las cargas P1, P2, y P3 tal como se muestra
en la figura…
A B
L = 5 m
P2 = 4 t P3 = 5 tP1 = 2 t
1 m 1 m2 m
Determinemos las reacciones de vínculo RA y RB
que equilibran el sistema…
       
 
 

















tR
tR
mRmPmPmPM
RRPPPF
F
B
A
BA
BAV
H
8,6
2,4
54310
0
0
321
321
Como todas las fuerzas exteriores son verticales, en
este caso, el esfuerzo axil N resulta nulo
0 N

6. (2)
(3)
Tracemos el
diagrama de corte…
Determinemos un funicular de polo O1 elegido de
modo que la línea de cierre (5) sea horizontal…
Resolución
RA = 4,2 t RB = 6,8 t
A B
L = 5 m
P2 = 4 t P3 = 5 tP1 = 2 t
1 m 1 m2 m
P1
P2
P3
RB
RA
Graficamos RA y RB en una escala conveniente…
Graficamos P1, P2 y P3 en la misma escala…
Trasladamos P1, P2, P3 , RA y RB sobre su
correspondiente línea de acción…
Trazamos el diagrama de corte Q …
Q
P2
RA
P1
P3
RB
O1
(1)
(4)
(5)

7. M
(2)
(3)
Tracemos el diagrama
de momento…
Resolución
P1
P2
P3
RB
RA
Q
P2
RA
P1
P3
RB
O1
(1)
(4)
(5)
El diagrama trazado con los lados (1), (2), (3) y (4)
del funicular, es el diagrama de momentos
flexores en escala de momentos que se construye
multiplicando la escala lineal por la escala de
fuerzas por la distancia polar ‘h’ del funicular.
(1)
(2)
(3)
(4)
h
Trazamos el diagrama de momentos M …

8. Bibliografía
Estabilidad II - E. Fliess
Introducción a la estática y resistencia de materiales - C. Raffo
Mecánica de materiales - F. Beer y otros
Resistencia de materiales - R. Abril / C. Benítez
Resistencia de materiales - Luis Delgado Lallemad / José M. Quintana Santana
Resistencia de materiales - V. Feodosiev
Resistencia de materiales - A. Pytel / F. Singer
Resistencia de materiales - S. Timoshenko

9. Muchas Gracias