Descargado 48 veces
Subido porGabriel Pujol
Sistemas Hiperestáticos
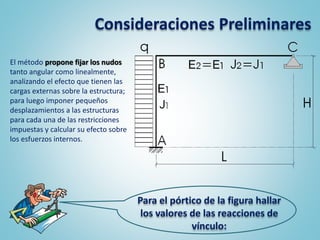
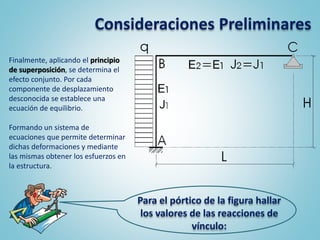
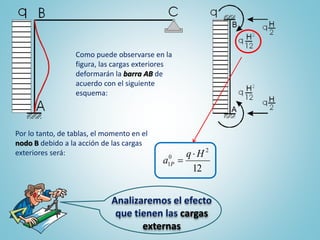
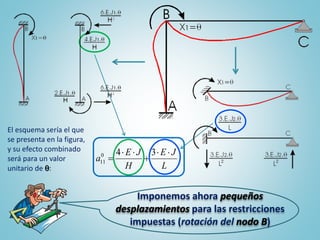
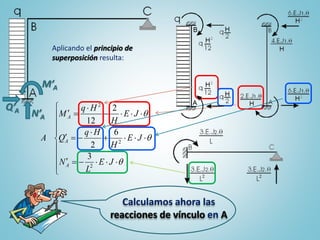
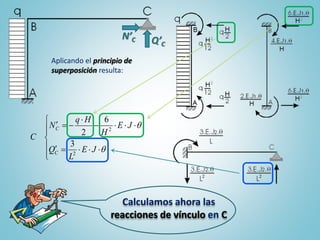
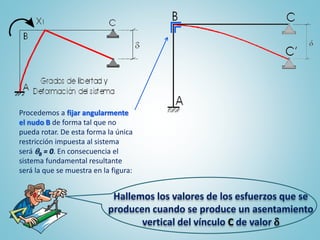
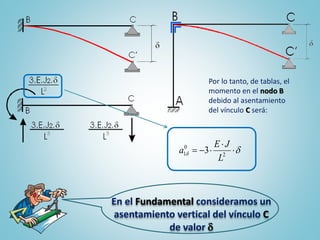
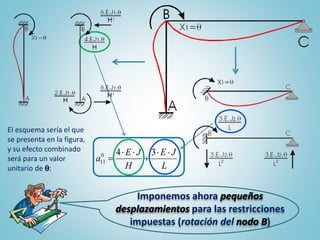
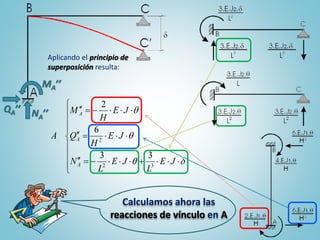
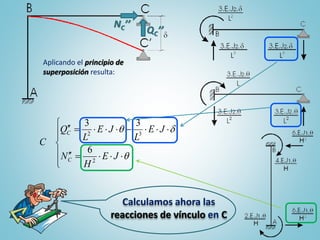
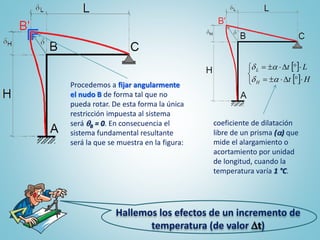
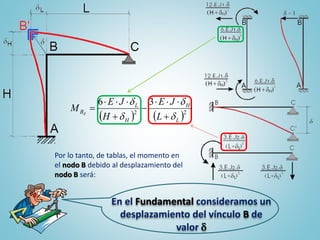
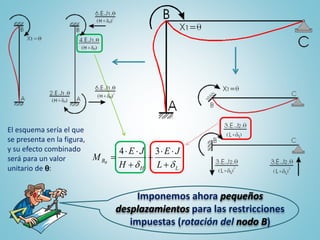
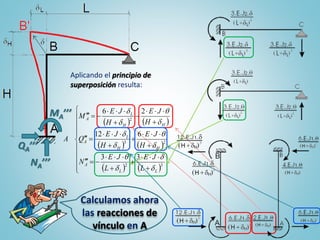
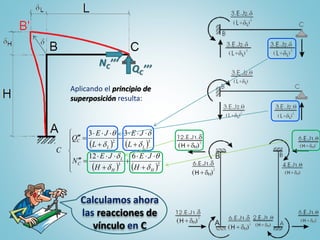
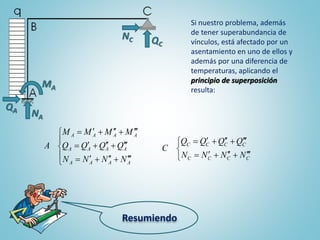
El documento presenta el ejercicio n° 4 de una guía sobre el método de las deformaciones en estructuras hiperestáticas, centrándose en la determinación de las reacciones de vínculo en un pórtico mediante la imposición de desplazamientos y el principio de superposición. Se analizan los efectos de las cargas externas y se establecen ecuaciones de equilibrio para calcular los esfuerzos internos en la estructura. Además, se consideran otros factores como asentamientos y diferencias de temperatura que afectan la estabilidad del sistema.
Más contenido relacionado
Similar a Sistemas Hiperestáticos
Sistemas Hiperestáticos
- 1. Hiperestáticos Método de lasDeformaciones Ejercicio N° 4 de la Guía de Problemas Propuestos Curso de Estabilidad IIb Ing. Gabriel Pujol Para las carreas de Ingeniería Mecánica e Ingeniería Naval y Mecánica de la Facultad de Ingeniería de la Universidad de Buenos Aires
- 2. Para el pórticode la figura hallar los valores de las reacciones de vínculo: Consideraciones Preliminares El método propone fijar los nudos tanto angular como linealmente, analizando el efecto que tienen las cargas externas sobre la estructura; para luego imponer pequeños desplazamientos a las estructuras para cada una de las restricciones impuestas y calcular su efecto sobre los esfuerzos internos.
- 3. Para el pórticode la figura hallar los valores de las reacciones de vínculo: Finalmente, aplicando el principio de superposición, se determina el efecto conjunto. Por cada componente de desplazamiento desconocida se establece una ecuación de equilibrio. Formando un sistema de ecuaciones que permite determinar dichas deformaciones y mediante las mismas obtener los esfuerzos en la estructura. Consideraciones Preliminares
- 4. Para el pórticode la figura hallar los valores de las reacciones de vínculo: Los esfuerzos en “pie de barras” están tabulados y podemos obtenerlos para vigas doblemente empotradas y empotradas/articuladas Consideraciones Preliminares
- 5. Definimos el Sistema Fundamental: Resolución Procedemosa fijar angularmente el nudo B de forma tal que no pueda rotar. De esta forma la única restricción impuesta al sistema será B = 0. En consecuencia el sistema fundamental resultante será la que se muestra en la figura y estará conformado por una barra empotrada-articulada (barra horizontal BC), y una barra empotrada-empotrada (barra vertical AB).
- 6. Definimos el Sistema Fundamental: Resolución Unavez hecho esto, analizaremos el efecto que tienen las cargas externas (q) sobre este sistema fundamental; para luego imponer pequeños desplazamientos a las estructuras para cada una de las restricciones impuestas (en este caso la rotación del nodo B) y calcular su efecto sobre los esfuerzos internos. Aplicando el principio de superposición, se determina el efecto conjunto.
- 7. Analizaremos el efecto quetienen las cargas externas Como puede observarse en la figura, las cargas exteriores deformarán la barra AB de acuerdo con el siguiente esquema: Por lo tanto, de tablas, el momento en el nodo B debido a la acción de las cargas exteriores será: 12 2 0 1 Hq a P
- 8. Imponemos ahora pequeños desplazamientospara las restricciones impuestas (rotación del nodo B) El esquema sería el que se presenta en la figura, y su efecto combinado será para un valor unitario de : L JE H JE a 340 11
- 9. Planteamos las ecuaciones decompatibilidad Como el sistema se encuentra en equilibrio, los momentos generados por la combinación de las cargas exteriores y los giros del nodo B deberán ser nulos: 00 11 0 1 aa P HLJE LHq HL HLJE Hq a a P 341234 12 3 2 0 11 0 1 Y obtenemos el valor del giro del nodo B:
- 10. Calculamos ahora las reaccionesde vínculo en A JE L N JE H Hq Q JE H Hq M A A A A 2 2 2 3 6 2 2 12 M’A Q’A N’A Aplicando el principio de superposición resulta:
- 11. Calculamos ahora las reaccionesde vínculo en C Q’C N’C Aplicando el principio de superposición resulta: JE L Q JE H Hq N C C C 2 2 3 6 2
- 12. Hallemos los valoresde los esfuerzos que se producen cuando se produce un asentamiento vertical del vínculo C de valor d Procedemos a fijar angularmente el nudo B de forma tal que no pueda rotar. De esta forma la única restricción impuesta al sistema será B = 0. En consecuencia el sistema fundamental resultante será la que se muestra en la figura:
- 13. En el Fundamentalconsideramos un asentamiento vertical del vínculo C de valor d Por lo tanto, de tablas, el momento en el nodo B debido al asentamiento del vínculo C será: dd 2 0 1 3 L JE a
- 14. Imponemos ahora pequeños desplazamientospara las restricciones impuestas (rotación del nodo B) El esquema sería el que se presenta en la figura, y su efecto combinado será para un valor unitario de : L JE H JE a 340 11
- 15. Planteamos las ecuaciones decompatibilidad Como el sistema se encuentra en equilibrio, los momentos generados por la combinación del asentamiento del vínculo C y los giros del nodo B deberán ser nulos: 00 11 0 1 d aa HLL H HL HLJE L JE a a 34 3 34 3 2 0 11 0 1 d d d d Y obtenemos el valor del giro del nodo B:
- 16. Calculamos ahora las reaccionesde vínculo en A MA’’ QA’’ NA’’ Aplicando el principio de superposición resulta: d JE L JE L N JE H Q JE H M A A A A 32 2 33 6 2
- 17. Calculamos ahora las reaccionesde vínculo en C QC’’ NC’’ Aplicando el principio de superposición resulta: d JE H N JE L JE L Q C C C 2 32 6 33
- 18. Hallemos los efectosde un incremento de temperatura (de valor t) Procedemos a fijar angularmente el nudo B de forma tal que no pueda rotar. De esta forma la única restricción impuesta al sistema será B = 0. En consecuencia el sistema fundamental resultante será la que se muestra en la figura: coeficiente de dilatación libre de un prisma () que mide el alargamiento o acortamiento por unidad de longitud, cuando la temperatura varía 1 °C. Ht Lt H L d d
- 19. En el Fundamentalconsideramos un desplazamiento del vínculo B de valor d Por lo tanto, de tablas, el momento en el nodo B debido al desplazamiento del nodo B será: 22 36 L H H L B L JE H JE M d d d d d
- 20. Imponemos ahora pequeños desplazamientospara las restricciones impuestas (rotación del nodo B) El esquema sería el que se presenta en la figura, y su efecto combinado será para un valor unitario de : LH B L JE H JE M dd 34
- 21. Planteamos las ecuaciones decompatibilidad Como el sistema se encuentra en equilibrio, los momentos generados por la combinación del desplazamiento del nodo B y los giros del nodo B deberán ser nulos: 0 d BB MM LH L H H L B B t L JE H JE L JE H JE M M dd d d d d d 34 36 22 Y obtenemos el valor del giro del nodo B:
- 22. Calculamos ahora las reaccionesde vínculo en A MA’’’ QA’’’ NA’’’ Aplicando el principio de superposición resulta: 32 23 2 33 612 26 LL A HH L A HH L A L JE L JE N H JE H JE Q H JE H JE M A d d d d d d d d d
- 23. 23 32 612 33 HH L C LL C H JE H JE N L JE L JE Q C d d d d d d Calculamos ahora las reacciones de vínculo en C Aplicando el principio de superposición resulta: QC’’’ NC’’’
- 24. Resumiendo AAAA AAAA AAAA NNNN QQQQ MMMM A MA QA NA Si nuestro problema,además de tener superabundancia de vínculos, está afectado por un asentamiento en uno de ellos y además por una diferencia de temperaturas, aplicando el principio de superposición resulta: QC NC CCCC CCCC NNNN QQQQ C
- 25. Bibliografía Estabilidad II -E. Fliess Introducción a la estática y resistencia de materiales - C. Raffo Mecánica de materiales - F. Beer y otros Resistencia de materiales - R. Abril / C. Benítez Resistencia de materiales - Luis Delgado Lallemad / José M. Quintana Santana Resistencia de materiales - V. Feodosiev Resistencia de materiales - A. Pytel / F. Singer Resistencia de materiales - S. Timoshenko
- 26.