Este documento presenta los conceptos fundamentales sobre columnas sometidas a flexión y compresión. Explica las fórmulas para calcular el pandeo de columnas con excentricidad y presenta las fórmulas de interacción para analizar la combinación de esfuerzos axiales y de flexión. Además, describe los tres casos considerados por el AISC para el análisis de flexión-compresión y cita las referencias bibliográficas clave sobre el tema.

1. COLUMNAS 3
PROYECTOS DE ACERO
FLEXO - COMPRESION
ING. WILLIAM LOPEZ
1
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA

2. FLEXO - COMPRESION
INTRODUCCIÓN
Hasta ahora hemos estudiado el caso de columnas
sometidas a carga axial o carga concéntrica, es
decir columnas inicialmente rectas y sin ninguna
excentricidad. Vamos a estudiar el tema de la
FLEXO - COMPRESION. Corresponde entonces a
continuación considerar el caso de columnas con
excentricidad, sea esta causada por
imperfecciones de la propia columnas o por
momentos aplicados. Generalmente en estos
casos el pandeo ocurre de inmediato, al aplicar el
momento P*e siendo “P” la carga y “e” la
excentricidad.
2
ING. WILLIAM LOPEZ
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA

3. FLEXO - COMPRESION
INTRODUCCIÓN
3
ING. WILLIAM LOPEZ
Figura 1. Columna con Excentricidad
y
P
L
P
δ
e
e
P
y
P
x
y
M= P*(e+y)
e
x
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA

4. FLEXO - COMPRESION
INTRODUCCIÓN - FORMULAS
Matemáticamente se resuelve este caso con la
llamada Formula de la Secante donde:
ymax = e*(sec (mL/2) -1)
donde m = √(P/E*I), o sea que
ymax = e*(sec (√(P/E*I)*(L/2) -1))
llegando finalmente, al aplicar Euler, a:
ymax = e*(sec (√(P/Pcr)*(π/2) -1))
y como el momento máximo ocurre en el centro de
“L” : M= P*(e + ymax)
Por lo que solo nos resta sustituir ymax en la
ecuación y donde el procedimiento de diseño
consistía en asumir un Fy y tomar un valor por
Norma. 4
ING. WILLIAM LOPEZ
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA

5. FLEXO - COMPRESION
INTRODUCCIÓN - FORMULAS
Para el calculo de columnas a FLEXO -
COMPRESION se emplean hoy día las Formulas de
Interacción que toman en cuenta la acción
simultanea de la carga axial y del momento flector
tanto en el rango elástico como en el rango plástico a
saber:
P/P0 + M/M0 ≤ 1
donde P y M = Carga Axial y Momentos actuantes
P0 y M0 = Resistencia a compresión simple y flexión
simple.
Usando factores adecuados se pueden escribir las
siguientes formulas. 5
ING. WILLIAM LOPEZ
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA

6. FLEXO - COMPRESION
INTRODUCCIÓN - FORMULAS
P/A*F.S. = fa = esfuerzo de trabajo bajo carga axial
de diseño
P0/A*F.S. = Fa = esfuerzo permisible por compresión
simple (como si solo existiese carga axial)
M/S*F.S. = fb = esfuerzo de trabajo por flexión bajo la
carga de diseño
M0/S*F.S. = Fb = esfuerzo permisible para flexión
pura (como si solo hubiesen momentos flectores)
Luego la formula de Interacción seria:
fa / Fa + fb / Fb ≤ 1
6
ING. WILLIAM LOPEZ
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA

7. FLEXO - COMPRESION
FORMULAS
7ING. WILLIAM LOPEZ
P
H
L
PL/2 L/2
δ
H/2H/2
Figura 2. Caso de la Viga - Columna
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA

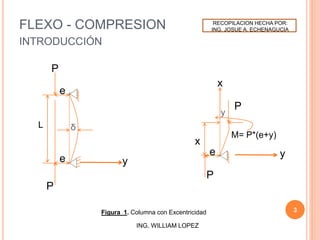
8. FLEXO - COMPRESION
INTRODUCCIÓN - FORMULAS
Ha sido demostrado en las vigas – columna que
y = y0(1/[1-(P/Pcr)]) donde
y0 = Flecha de la viga sin carga axial (por
imperfección, excentricidad, flecha inicial, etc.)
P = Carga axial actuante
Pcr = Carga critica de Euler
1/[1-(P/Pcr)] = Factor de Amplificación
Por consiguiente si en la viga actúa un momento
inicial Mb debido a carga otro efecto implica que:
M = Mb* Factor de Amplificación
8
ING. WILLIAM LOPEZ
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA

9. FLEXO - COMPRESION
INTRODUCCIÓN - FORMULAS
Entonces nos queda la formula de Interacción de la
siguiente manera:
P/P0 + Mb /M0*Factor de Amplificación ≤ 1
El American Institute for Steel Construction (A.I.S.C.)
considera tres (03) casos:
Caso I : Cuando la carga axial es pequeña y se permite
no tomar en cuenta el factor de amplificación y cuando
la carga axial es apreciable. Es decir:
fa / Fa + fb / Fb ≤ 1 cuando fa / Fa ≤ 0,15
9
ING. WILLIAM LOPEZ
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA

10. FLEXO - COMPRESION
INTRODUCCIÓN - FORMULAS
Caso II: Cuando fa / Fa ≥ 0,15 quedaría de la siguiente
manera:
fa / Fa + Cm*fb /(1-fa/Fe’)*Fb ≤ 1
donde:
Cm = αm (Norma) = Factor de equivalencia que toma en
cuenta las diferentes condiciones de apoyo y tipos de
carga. Para el caso que nos ocupa Flexo – Compresión:
10
ING. WILLIAM LOPEZ
M2
L
M1 M2 > M1
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA

11. FLEXO - COMPRESION
INTRODUCCIÓN - FORMULAS
Caso II: Para casos con desplazamiento lateral (pórticos
no arriostrados lateralmente):
Cm = αm (Norma) = 0,85 (fijo)
Fe’ = Esfuerzo critico (Rango Elástico, Euler)
Fe’ = fcr/F.S.
Para casos sin desplazamiento lateral (pórticos
arriostrados lateralmente):
Cm = αm (Norma) = 0,6 –(0,40)(M1/M2) ≥ 0,40 (No menor
que 0,4)
11
ING. WILLIAM LOPEZ
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA

12. FLEXO - COMPRESION
INTRODUCCIÓN - FORMULAS
Caso III : Cuando fa / Fa > 0,15 en puntos arriostrados en el
plano de flexión. Es decir:
fa /0,6Fy + fb / Fb ≤ 1
Este caso esta previsto para vigas-columna donde la
máxima combinación de esfuerzos por carga axial y flexión
pueden mantenerse en un extremo arriostrado y no en los
puntos intermedios del miembro donde se magnifican los
momentos. En la Norma COVENIN, pagina 35 se hallan
estas mismas formulas expresadas en los casos en los que
hay flexión en ambos sentidos ortogonales. Según la Norma
COVENIN
Fe’ = 10.8x106/(K*Lb/rb)2
y donde Lb = es la longitud no arriostrada en el plano de la
flexión y rb es el correspondiente radio de giro.
12
ING. WILLIAM LOPEZ
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA

13. FLEXO - COMPRESION
BIBLIOGRAFIA:
 Norma Venezolana COVENIN 1618-82: Estructuras de
Acero para Edificaciones, Proyectos, fabricación y
construcción.
 “Specification for the Design, Fabrication and Erection
of Structural Steel for Buildings” del American Institute
of Steel Construction (AISC).
 “Strength of Materials” (Resistencia de Materiales) de
Ferdinand L. Singer.
13
ING. WILLIAM LOPEZ
RECOPILACION HECHA POR:
ING. JOSUE A. ECHENAGUCIA