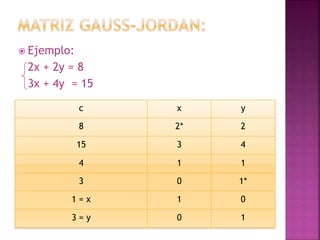
Un sistema de ecuaciones lineales consiste en dos o más ecuaciones lineales con las mismas incógnitas. El documento explica que un sistema puede tener una solución única, infinitas soluciones o ninguna solución dependiendo de si las razones de los coeficientes son iguales o diferentes. Además, describe métodos como sustitución, igualación, reducción y el método de Gauss para resolver sistemas de ecuaciones lineales.

2. Un Sistema de Ecuaciones Lineales es un conjunto
de ecuaciones lineales con incógnitas comunes.
Se pueden representar de esta manera:
a1x+ b1y + c1 =0
a2x+ b2y + c2 =0
Ejemplos de un Sistema de Ecuaciones Lineales
x + 4y = 34
3x - 3y = 24
23x + 63y = 15
27x + 45y = 35

3.  Si a1/a2 es diferente a b1/b2, entonces el sistema
tiene una solución.
 Si a1/a2 es igual a b1/b2, pero b1/b2 es diferente
c1/c2, entonces el sistema no tiene solución.
 Si a1/a2 es igual a b1/b2, y b1/b2 es igual a c1/c2,
entonces el sistema tiene un número infinito de
soluciones.

4. Existen varias formas de resolver un
Sistema de Ecuaciones, entre ellas
están:
Tradicionales (sustitución, igualación,
reducción o alguna mezcla de estos).
Método de Gauss-Jordan o solo método
Gauss.

5. Dependiendo de las circunstancias,
podemos proceder de las siguientes
maneras:
-Sustitución:
Se procede a hallar uno de los términos
en función del otro, de preferencia usar
el de menor coeficiente, y luego se
reemplaza en la siguiente ecuación.

6. -Igualación:
Derivado de la Sustitución, se procede a
despejar la misma incógnita en las dos
ecuaciones y a continuación se igualan la
parte derecha de ambas ecuaciones.
-Reducción:
Se procede de la siguiente manera:
Mediante productos procuramos que las
ecuaciones tengan una incógnita con el
mismo coeficiente y signo distinto. Lugo
sumamos las ecuaciones y se despejará la
incógnita.

7. Consiste en un método de
eliminación mediante matrices,
mediante el cual podemos hallar las
incógnitas mediante
transformaciones elementales,
hasta obtener valores de una sola
incógnita donde el valor de cada
incógnita será igual al del
coeficiente en la misma fila de la
matriz.

8.  Ejemplo:
2x + 2y = 8
3x + 4y = 15
c x y
8 2* 2
15 3 4
4 1 1
3 0 1*
1 = x 1 0
3 = y 0 1

9. 1)Hallar cuantas soluciones tiene el siguiente
Sistema de ecuaciones:
5x + 3y + 3=0
10x + 6y + 5=0
Solución
5/10 = 3/6
3/6 ≠ 3/5
-El C.S. del sistema es nulo, por lo tanto no
presenta ninguna solución

10. 2)Hallar cuantas soluciones tiene el siguiente
Sistema de ecuaciones:
7x + 36y =40
12x - 15y =2
Solución
7/12 ≠ 36/-15
36/-15≠ 40/2
-El C.S. del sistema es único, presenta solo una
solución.

11. 3)Resuelve por igualación:
5x + y =12
7x + y = 22
Solución
(I) … y = 12 – 5x 12 – 5x = 22 – 7y
(II) … y = 22 – 7y 2x = 10
x = 5
5(5) + y = 12
y = -13
Rpta.- x= 5, y = -13

12. 4)Resuelve por reducción:
6x + 8y = 2
4x - 8y = -4
Solución
6x + 8y = 2 6(-0.2) + 8y = 2
4x – 8y = -4 -1.2 + 8y = 2
10x = -2 8y = 3.2
x = -0.2 y = 0.4
Rpta.- x = -0.2, y = 0.4

13. 5)Resuelve por Gauss:
2x + 5y = 19
5x + 4y = 22
c x y
19 2* 5
22 5 4
19/2 1 5/2
-51/2 0 -17/2*
2 1 0
3 0 1
Rpta.- x = 2, y = 3