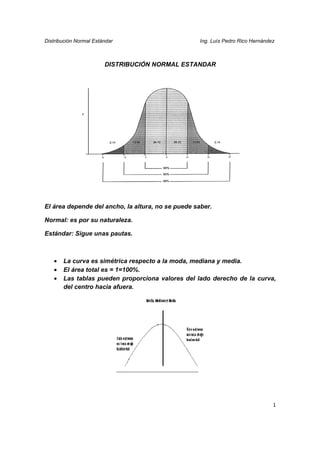
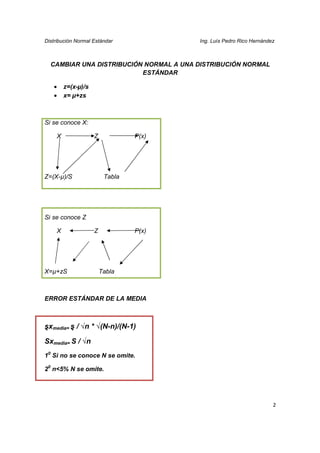
La distribución normal estándar describe cómo ciertas variables aleatorias se distribuyen de forma simétrica alrededor de una media. El documento proporciona ejemplos de cómo calcular probabilidades utilizando la distribución normal estándar para variables como la vida útil de componentes, el peso de paquetes de cereal y el tiempo requerido para tareas. También explica cómo convertir una distribución normal a una distribución normal estándar.

1. Distribución Normal Estándar Ing. Luís Pedro Rico Hernández
DISTRIBUCIÓN NORMAL ESTANDAR
El área depende del ancho, la altura, no se puede saber.
Normal: es por su naturaleza.
Estándar: Sigue unas pautas.
• La curva es simétrica respecto a la moda, mediana y media.
• El área total es = 1=100%.
• Las tablas pueden proporciona valores del lado derecho de la curva,
del centro hacia afuera.
1

2. Distribución Normal Estándar Ing. Luís Pedro Rico Hernández
CAMBIAR UNA DISTRIBUCIÓN NORMAL A UNA DISTRIBUCIÓN NORMAL
ESTÁNDAR
• z=(x-µ)/s
• x= µ+zs
Si se conoce X:
X Z P(x)
Z=(X-µ)/S Tabla
Si se conoce Z
X Z P(x)
X=µ+zS Tabla
ERROR ESTÁNDAR DE LA MEDIA
ȿxmedia= ȿ / √n * √(N-n)/(N-1)
Sxmedia= S / √n
10 Si no se conoce N se omite.
20 n<5% N se omite.
2

3. Distribución Normal Estándar Ing. Luís Pedro Rico Hernández
DISTRIBUCIÓN DE PROBABILIDAD PARA VARIABLES ALEATORIA
CONTINUA NORMAL
Z= (x - µ)/s
X= µ+zs
1. Se sabe que el ciclo de vida de un componente eléctrico sigue una
distribución normal con una media de µ=2 000 horas y una desviación
estándar S= 200 horas. ¿Cuál es la probabilidad de que un componente
aleatoriamente seleccionado durante 2 000 y 2 400 horas.
2. En relación con los componentes electrónicos descritos en el ejemplo
anterior, supongamos que nos interesa la probabilidad de que un
componente aleatoriamente seleccionado dure más de 2,200 horas.
334
3. El proceso de empaque de una compañía productora de cereales para el
desayuno ha sido ajustado para que cada paquete contenga un promedio
de µ=13.0 onzas de cereal. Por supuesto que no todos los paquetes
contienen exactamente 13.0 oz, a causa de fuetes aleatorias de
probabilidad. La desviación estándar del peso real es s=0.1 oz. Y se sabe
que la distribución de peso sigue la distribución normal de probabilidad.
Determine la probabilidad de que un paquete aleatoriamente seleccionado
contenga entre 13.0 oz y 13.2 oz de cereal e ilustre la proporción de área
bajo la curva asociada con este valor de probabilidad.
4. Respecto de la situación descrita en el ejemplo anterior ¿Cuál es la
probabilidad de que el peso del cereal exceda de 13.25 oz? Ilustre la
proporción del área bajo la curva normal relevante a este caso.
5. En relación con el problema del ejercicio de empaque de cereal. ¿Cuál es la
probabilidad de que el peso del cereal se halle entre 12.9 y 13.1 oz?
6. ¿Cuál es la probabilidad de que el peso del cereal se halle entre 12.8 y 13.1
oz? Ilustre el área bajo la curva relevante a este caso.
7. ¿Cuál es la probabilidad de que el peso del cereal se halle entre 13.1 y 13.2
oz? Ilustre la proporción de área bajo la curva relevante en este caso.
8. La cantidad requerida para el servicio rutinario a la transmisión de un
automóvil tiene una distribución normal con µ=45 min. y S=8.0 min. El
3

4. Distribución Normal Estándar Ing. Luís Pedro Rico Hernández
gerente del servicio planea el inicio de labores en la transmisión del auto
estará listo en una hora. ¿Cuál es la probabilidad de que el gerente de
servicio esté equivocado? Ilustre la proporción de área bajo la curva
relevante para este caso.
9. En referencia al problema anterior. ¿Cuál sería la asignación de tiempo real
requerido a fin de que haya un 75% de probabilidad de que el servicio de
transmisión se lleve a cabo en ese tiempo? Ilustre la proporción de área
relevante.
10. ¿Cuál sería la asignación de tiempo laboral a fin de que haya una
probabilidad de solo 30% de que el servicio de transmisión se lleve a cabo
en ese tiempo? Ilustre la proporción de área.
11. Las calificaciones reportadas en una prueba de aprovechamiento de
vigencia nacional para graduados de preparatoria tiene una media de
µ=500 con desviación estándar S= 100 La distribución de calificaciones es
aproximadamente normal. ¿Cuál es la probabilidad de que la calificación de
un individuo aleatoriamente elegido se encuentre:
a) Entre 500 y 650
b) Entre 450 y 600
12. Las calificaciones reportadas en una prueba de aprovechamiento de
vigencia nacional para graduados de preparatoria tiene una media de
µ=500 con desviación estándar S= 100. ¿Cuál es la probabilidad de que un
individuo aleatoriamente elegido tenga una calificación
a) Inferior a 300
b) Superior a 650
13. Se ha determinado que la vida útil de cierta marca de llantas de alto
rendimiento sigue una distribución normal con media µ=38 000 millas y S=
3 000 millas:
a) ¿Cuál es la probabilidad de que una llanta aleatoriamente seleccionada
tenga una vida útil de al menos 35 000 millas?
b) ¿Cuál es la probabilidad de que dure más de 45 000 millas?
c)
4

5. Distribución Normal Estándar Ing. Luís Pedro Rico Hernández
14. Se ha determinado que la cantidad de tiempo requerida por un individuo en
la ventanilla de un banco con distribución normal con µ=130 seg. y S= 45
seg. ¿Cuál es la probabilidad de que un individuo aleatoriamente
seleccionado:
a) Requiera de menos de 100 seg. para concluir una transacción.
b) Pase entre 2 y 3 minutos en la ventanilla.
15. En una fabrica muy grande el salario de los trabajadores tiene un promedio
de$9 600 y S= $1 800. Determine las siguientes probabilidades.
a) De que su salario sea mayor de $10 000
b) Que su salario este entre $1 800 y $11 000
c) Que su salario sea mayor de $7 500
d) Que su salario este entre $9 600 y $10 000
e) De que su salario este entre $10 000 y $12 000
Bibliografía
Estadística aplicada a la administración y economía
Leonard J. Kazmier
Tercera edición 1998
México D.F.
Mc Graw Hill
5