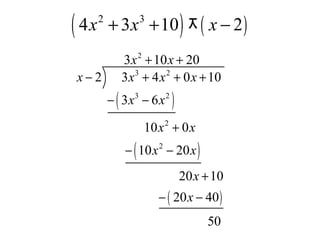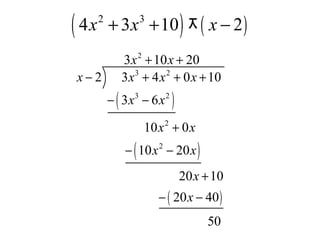
Este documento describe métodos para dividir polinomios, incluyendo división larga, división sintética y sustitución sintética. Explica cómo utilizar división sintética para dividir polinomios y binomios lineales, y cómo aplicar el teorema del residuo. También proporciona ejemplos de cómo usar sustitución sintética para evaluar polinomios para valores dados.

1. Sección 6 – 3 Dividiendo Polinomios Álgebra 2 Noveno Grado

2. Warm Up

3. Objetivos Utilizar división larga y división sintética para dividir polinomios.

4. Utilizando División Larga para Dividir Polinomios

6. División Sintética Para que funcione la división sintética, el polinomio debe estar escrito en forma estándar, utilizando 0 como coeficiente para cualquier término perdido y el divisor tiene que ser de la forma x – a . Divide (2x 2 + 7x + 9) ÷ (x + 2) utilizando división sintética.

7. Utilizando División Sintética para Dividir Binomios Lineales

8. Teorema del Residuo Si la función polinomial P ( x ) es dividida por x – a , entonces el residuo r es P ( a ).

9. Utilizando Sustitución Sintética Utiliza sustitución sintética para evaluar el polinomio para el valor dado. P(x) = x 3 – 4x 2 + 3x – 5 para x = 4 P(x) = 4x 4 + 2x 3 + 3x + 5 para x = - ½ P(x) = x 3 + 3x 2 + 4 para x = -3 P(x) = 5x 2 + 9x + 3 para x = 1/5 P(x) = 2x 3 + 5x 2 – x + 7 para x = 2

10. Asignación Página 426 Ejercicios 14 – 28 (pares)