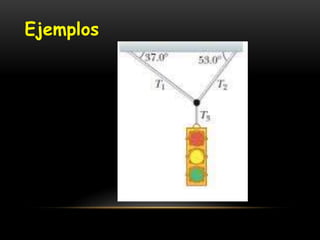
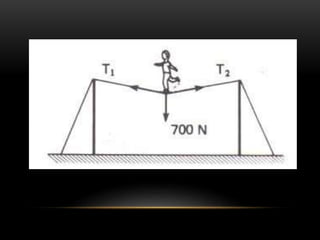
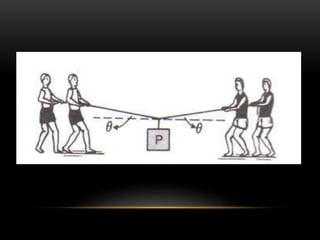
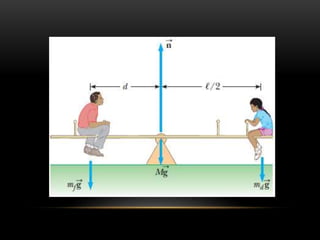
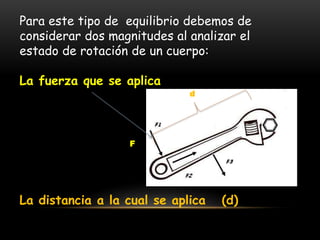
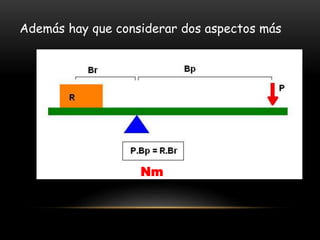
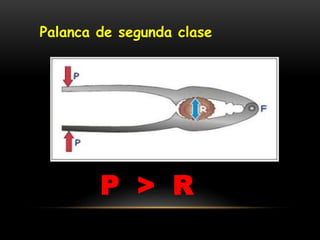
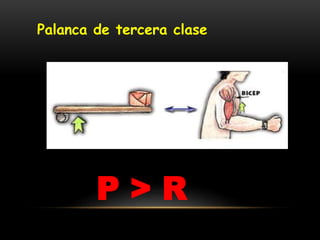
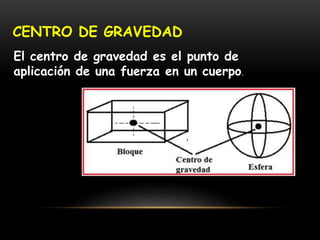
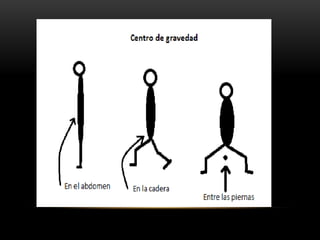
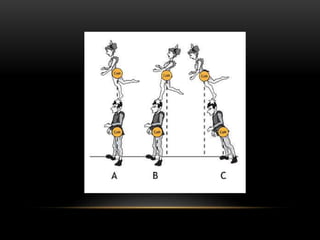
Este documento describe los conceptos de equilibrio traslacional y rotacional. Explica que el equilibrio traslacional requiere que la suma de fuerzas en los ejes vertical y horizontal sea cero, mientras que el equilibrio rotacional depende de la fuerza aplicada y su distancia al eje de rotación. Incluye ejemplos de ambos tipos de equilibrio y conceptos como momento de torsión, brazo de palanca, centro de gravedad y centro de masa. El objetivo es que los estudiantes comprendan estos conceptos y puedan

1. Traslacional y rotacional
EQUILIBRIO

2. Unidad 2
Mtra. Ortega Cruz María Luisa Edith
Plantel : CONALEP – Chipilo
Periodo escolar: Agosto – Diciembre 2016
Módulo: Interpretación de Fenómenos
Físicos de la Materia
Elaborado: 16 de Agosto 2016

3. PROPÓSITO
Identificará y analizará
situaciones de estática
relacionadas con el entorno,
empleando las ecuaciones que
rigen el reposo para resolver
problemas relacionados con el
equilibrio

4. Justificación
El desarrollo del presente
trabajo es con el motivo de que el
estudiante comprenda el
concepto de “equilibrio”
traslacional y rotacional mediante
ejemplos que ve en su vida
cotidiana

5. Resultado de Aprendizaje 2.1
Determina el equilibrio
traslacional de un cuerpo en una
situación cotidiana mediante el
calculo de la fuerza requerida y
su representación grafica
través de un vector

6. EQUILIBRIO
Cuerpo en
equilibrio, la suma
vectorial de todas
las fuerzas que
actúan sobre él
debe ser igual a
cero.
Cumple dos
condiciones:

7. EQUILIBRIO
TRASLACIONAL
la sumatoria de fuerzas
concurrentes tanto en
el eje vertical como en
el horizontal debe ser
igual a cero

8. Ejemplos

11. Resultado de aprendizaje 2.2
Demuestra las condiciones del
equilibrio rotacional en
situaciones de la vida cotidiana a
través del calculo de la fuerza
resultante y su representación
vectorial.

12. EQUILIBRIO ROTACIONAL
Movimiento con el que estamos en contacto todos
los días, ya que lo que provoca que un cuerpo rote
son varias fuerzas que actúan sobre éste.

13. En la rotación, hay un punto (o un
eje) que permanece fijo y el sistema
gira alrededor de él

14. Ejemplos

17. Para este tipo de equilibrio debemos de
considerar dos magnitudes al analizar el
estado de rotación de un cuerpo:
La fuerza que se aplica
La distancia a la cual se aplica (d)
d
F

18. Para resolver este tipo de problemas,
utilizaremos varios conceptos y la condición
de equilibrio.
La condición de equilibrio nos dice que:
 = 0

19. BRAZO DE PALANCA
Maquina simple que tiene como función
transmitir una fuerza y un desplazamiento.
Se compone de
fulcro potencia
resistencia

20. Además hay que considerar dos aspectos más
Nm

21. Tipos de palanca

22. Palanca de primera clase
P < R

23. Palanca de segunda clase
P > R

24. Palanca de tercera clase
P > R

25. MOMENTO DE TORSIÓN
Tendencia a producir un cambio en el
movimiento rotacional.
También es conocido como momento de fuerza

26. El movimiento rotacional se ve afectado
tanto por la magnitud de una fuerza como
por su brazo de palanca, por lo que
 = Fxr

27. PAR DE FUERZAS
Sistema de dos fuerzas paralelas, de igual
intensidad y de sentido contrario, capaces
de producir en su momento una rotación.
M = F1x d = F2 x d

28. CENTRO DE GRAVEDAD
El centro de gravedad es el punto de
aplicación de una fuerza en un cuerpo.

30. CENTRO DE MASA
El centro de masa de un sistema discreto o
continuo es el punto geométrico que se
comporta como si en él estuviera aplicada la
resultante de las fuerzas externas del
sistema.
Se puede decir que esta formado por toda la
masa concentrada en el centro

32. Ejercicios