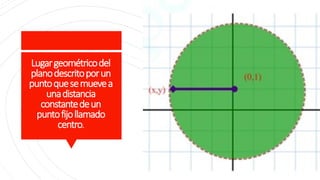
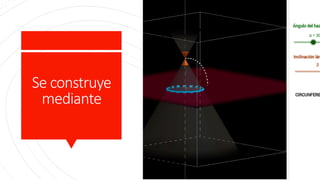
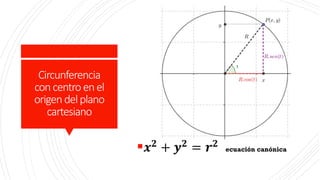
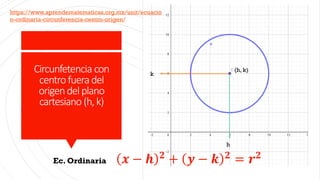
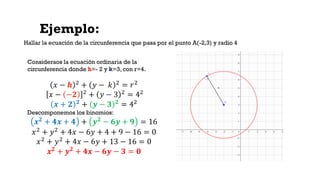
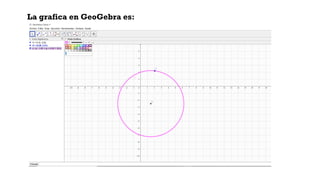
Este documento describe la circunferencia como el lugar geométrico formado por los puntos que se encuentran a una distancia constante de un punto fijo llamado centro. Explica cómo construir circunferencias mediante sus ecuaciones canónicas y ordinarias, y cómo hallar el centro y radio a partir de la ecuación general de una circunferencia. Finalmente, proporciona ejemplos y ejercicios prácticos sobre el cálculo de ecuaciones de circunferencias.

1. LA CIRCUNFERENCIA
MTRA. Ma. Luisa Ortega Cruz

2. Unidad 2
Mtra. Ortega cruz María Luisa Edith
Plantel: CONALEP – Chipilo
Periodo escolar: Agosto-Diciembre 2019
Módulo: Manejo de espacios y cantidades
Elaborado: 20 de agosto 2019

3. Propósito
Representar gráficamente
fenómenos naturales y/o sociales
mediante el cálculo de
superficies, distancias,
pendientes y ángulos
relacionados con su vida diaria a
fin de construir lugares
geométricos que permitan la
ubicación de objetos en sistemas
coordenados

4. Unidad de
aprendizaje 2
Integración de los
lugares geométricos
generados a partir
de un cono

5. Resultado de
aprendizaje 2.2
Interpreta las
relaciones algebraicas
de los cortes con los
elementos y
ecuaciones que
integran un cono

6. 2.2.1
Circunferencia

7. Lugargeométricodel
planodescritoporun
puntoquesemuevea
unadistancia
constantedeun
puntofijollamado
centro.

8. Se encuentra
en:

9. Se construye
mediante

10. Circunferencia
concentro enel
origen delplano
cartesiano
▪ 𝒙 𝟐 + 𝒚 𝟐 = 𝒓 𝟐 ecuación canónica

11. Circunfetencia con
centrofueradel
origendelplano
cartesiano (h,k)
𝒙 − 𝒉 𝟐
+ 𝒚 − 𝒌 𝟐
= 𝒓 𝟐
Ec. Ordinaria
(h, k)
k
h
https://www.aprendematematicas.org.mx/unit/ecuacio
n-ordinaria-circunferencia-centro-origen/

12. Ejemplo:
Hallar la ecuación de la circunferencia que pasa por el punto A(-2,3) y radio 4
Consideraos la ecuación ordinaria de la
circunferencia donde h=- 2 y k=3, con r=4.
𝑥 − 𝒉 2
+ 𝑦 − 𝑘 2
= 𝑟2
𝑥 − −𝟐 2
+ 𝑦 − 3 2
= 42
𝒙 + 𝟐 𝟐 + 𝒚 − 𝟑 𝟐 = 42
Descomponemos los binomios:
𝒙 𝟐
+ 𝟒𝒙 + 𝟒 + 𝒚 𝟐
− 𝟔𝒚 + 𝟗 = 16
𝑥2 + 𝑦2 + 4𝑥 − 6𝑦 + 4 + 9 − 16 = 0
𝑥2 + 𝑦2 + 4𝑥 − 6𝑦 + 13 − 16 = 0
𝒙 𝟐
+ 𝒚 𝟐
+ 𝟒𝒙 − 𝟔𝒚 − 𝟑 = 𝟎

13. Ecuación
general de la
circunferencia
▪ 𝑨𝒙 𝟐
+ 𝑩𝒚 𝟐
+ 𝑫𝒙 + 𝑬𝒚 + 𝑭 = 𝟎
▪ 𝐶 = −
𝐷
2
, −
𝐸
2
▪ 𝑟 =
1
2
𝐷2 + 𝐸2 − 4𝐹
▪ Donde, si:
▪ 𝐷2 + 𝐸2 − 4𝐹 > 0, la circunferencia es real
▪ 𝐷2 + 𝐸2 − 4𝐹 < 0, la circunferencia es imaginaria
▪ 𝐷2
+ 𝐸2
− 4𝐹 = 0 el radio es cero y la ecuación
representa el punto −
𝐷
2
, −
𝐸
2

14. Ejemplo:
𝒙 𝟐
+ 𝒚 𝟐
+ 𝟒𝒙 − 𝟔𝒚 − 𝟑 = 𝟎
Si consideramos la ecuación de la circunferencia anterior:
Identificamos las variables de acuerdo a la ecuación general como:
A = 1
B = 1
D = 4
E = - 6
F = - 3

15. Si tomamos el caso contrario donde partimos de la ecuación general podemos encontrar el centro y
radio de la circunferencia,es decir:
𝑥2
+ 𝑦2
− 3𝑥 + 5𝑦 − 14 = 0
𝑥2
− 3𝑥 + 2
+ 𝑦2
+ 5𝑦 + 2
= 14
En este paso lo que se hará es completar el trinomio cuadrado perfecto, y el termino a incrementar
deberá hacerse de ambos lados de la ecuación para que esta se mantenga.
𝑥2 − 3𝑥 +
−3
2
2
+ 𝑦2 + 5𝑦 +
+5
2
2
= 14 +
−3
2
2
+
+5
2
2
𝑥2
− 3𝑥 +
9
4
+ 𝑦2
+ 5𝑦 +
25
4
= 14 +
9
4
+
25
4
𝑥 −
3
2
2
+ 𝑦 +
5
2
2
=
90
4
Por lo que el centro es 𝐶 =
3
2
, −
5
2
y radio es 𝑟 =
90
4
=
45
2
entonces 𝑟 =
45
2

16. La grafica en GeoGebra es:

17. Practica

18. 1.Hallar la ecuación de la circunferencia cuyo centro es
C(1, 5) que pasa por el punto P(-3,2)
2.Hallar la ecuación de la circunferencia cuyo diámetro
es el segmento de extremos cuyos puntos son: A(2, 3)
y B(-4, -9)
3.Hallar la ecuación de la circunferencia que pasa por 3
puntos D(0,0), E(0,5, F(3,2
4.Hallar el centro y el radio de la circunferencia que
tiene por ecuación:
𝑥2 + 𝑦2 + 2𝑥 − 4𝑦 − 4 = 0

19. Para resolver un sistema de tres ecuaciones
con 3 variables podemos usar dos métodos:
a) El método de determinantes
b) La regla de Crammer
Tips

20. Determinantes