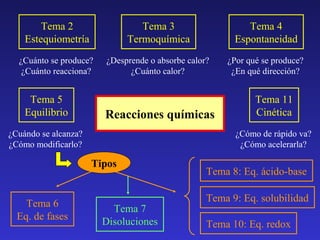
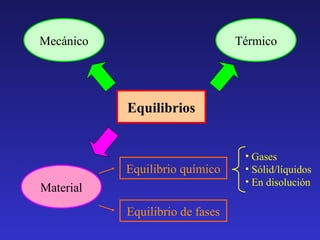
El documento presenta un resumen de 11 temas relacionados con la química de equilibrios. Los temas incluyen equilibrio químico, termoquímica, espontaneidad de reacciones, cinética química, equilibrios de fases, disoluciones, equilibrios ácido-base, equilibrios de solubilidad y redox. Cada tema presenta conceptos clave y ejemplos relevantes.

1. El equilibrio en las
reacciones químicas

2. Tema 2
Estequiometría
Tema 3
Termoquímica
Tema 4
Espontaneidad
¿Cuánto se produce?
¿Cuánto reacciona?
¿Desprende o absorbe calor?
¿Cuánto calor?
¿Por qué se produce?
¿En qué dirección?
Tema 5
Equilibrio
Reacciones químicas
¿Cuándo se alcanza?
¿Cómo modificarlo?
¿Cómo de rápido va?
¿Cómo acelerarla?
Tipos
Tema 6
Eq. de fases
Tema 11
Cinética
Tema 7
Disoluciones
Tema 8: Eq. ácido-base
Tema 9: Eq. solubilidad
Tema 10: Eq. redox

3. Mecánico
Térmico
Equilibrios
Equilibrio químico
Material
Equilibrio de fases
• Gases
• Sólid/líquidos
• En disolución

4. CONTENIDO
1.- Aspectos básicos del equilibrio químico.
2.- Condición general del equilibrio químico.
3.- Equilibrio químico en sistemas gaseosos ideales.
4.- Equilibrios heterogéneos.
5.- Variación de la constante de equilibrio con la temperatura.
6.- Respuesta del equilibrio a un cambio de condiciones.
Principio de Le Châtelier.

5. 1
ASPECTOS BÁSICOS DEL EQUILIBRIO
QUÍMICO.
Estado de equilibrio: estado en que la composición
del sistema permanece fija.
1.1. Perspectiva cualitativa.
• Equilibrio dinámico.
• Los sistemas evolucionan espontáneamente hacia un
estado de equilibrio.
• Las propiedades del estado de equilibrio son las mismas,
independientemente de la dirección desde la que se alcanza.
1.2. Perspectiva cuantitativa.
Ley de acción de masas
aA + bB ↔ cC + dD
[ C] c [ D ] d
[ A] a [ B] b
= constante

6. 2
CONDICIÓN GENERAL DEL
EQUILIBRIO QUÍMICO.
A P y T constantes, el sentido del cambio espontáneo es el sentido
de la disminución de G.
Proceso espontáneo: ∆G < 0
[Tema 4]
∆G = ∑ G(prod) − ∑ G (reac)
prod
Inicio: ∆G < 0
reac
∑ G(prod) < ∑ G (reac)
prod
reac
Equilibrio: ∆ G = 0
∑ G(prod) = ∑ G (reac)
prod
reac
[Tema 4]

7. 3
EQUILIBRIO QUÍMICO EN SISTEMAS
GASEOSOS IDEALES.
EQUILIBRIO HOMOGÉNEO
∆G = ∑ G(prod) − ∑ G (reac) = cG C + dG D − aG A − bG B
prod
reac
Pi
Para una mezcla de gases ideales: G i = G + RT ln
Pº
o
i
o
o
o
o
∆G = cG C + dG D − aG A − bG B + cRT ln
c
[Levine, pg 175-177]
PC
P
P
P
+ dRT ln D − aRT ln A − bRT ln B
Pº
Pº
Pº
Pº
d
 PC   PD 
   
 Pº   Pº 
∆G = ∆Gº + RT ln
a
b
 PA   PB 
   
 Pº   Pº 
Q : Cociente de reacción
∆G = ∆Gº + RT ln Q
Isoterma de reacción

8. Cuando lleguemos al equilibrio: ∆G = 0
  PC  c  PD  d 
    
Pº
Pº
∆G = ∆Gº + RT ln    a  b  = 0
  PA   PB  
    
  Pº   Pº   eq
Kpº
Constante de equilibrio
termodinámica
(adimensional)
∆Gº + RT ln K o = 0 ; ∆G º = −RT ln K o
p
p
K =e
o
p
− ∆G º / RT

9. K =e
o
p
− ∆G º / RT
Consecuencias:
• Si ∆Gº >> 0 ; Kpº << 1 : poca tendencia r → p
• Si ∆Gº << 0 ; Kpº >> 1 : mucha tendencia r → p
• Kpº > 0 y depende de ∆Gº
• ∆Gº sólo depende de T; Kpº también.
• Disponemos de dos formas de determinar Kpº
  PC  c  PD  d 
    
Pº
Pº
K o =    a  b 
K o = e − ∆G º / RT
p
p
  PA   PB  
    
  Pº   Pº   eq

10. ¿Hacia dónde evoluciona la reacción?
Q
∆G = −RT ln K + RT ln Q = RT ln o
Kp
o
p
∆G = ∆Gº + RT ln Q
∆G º = −RT ln K o
p
• Si Q < Kpº
∆G < 0
r → p espontánea
• Si Q > Kpº
∆G > 0
r → p no espontánea
(p → r espontánea)
• Si Q = Kpº
∆G = 0
Equilibrio

11. Otras expresiones de la constante de equilibrio
  PC  c  PD  d 
    
 ( PC ) c ( PD ) d 
Pº   Pº  
Ko = 
=
p
a
b
a
b
  PA   PB  
 ( PA ) ( PB )  eq
    
  Pº   Pº   eq
(dimensional)
[ C] c [ D] d
Kc =
a
b
[ A ] [ B]
Si ∆n = 0
d
1 1
   
 Pº   Pº 
a
b
1 1
   
 Pº   Pº 
Kp
En función de las concentraciones:
c
(Pº)-∆n
[Petrucci, pg 635]
Kp = Kc (RT)∆n
Kpº = Kp = Kc

12. 4
EQUILIBRIOS HETEROGÉNEOS.
Aquéllos en los que las sustancias están en fases distintas
p.ej.: CaCO3 (s) ↔ CaO (s) + CO2 (g)
La situación de equilibrio no se ve afectada por la cantidad de
sólido o líquido, siempre y cuando estas sustancias estén presentes.
La constante de equilibrio es independiente de las cantidades
de sólidos y líquidos en el equilibrio.
CaCO3 (s) ↔ CaO (s) + CO2 (g)
Kc = [CO2]

13. 5
VARIACIÓN DE LA CONSTANTE DE
EQUILIBRIO CON LA TEMPERATURA.
¿Cómo podemos modificar la situación de equilibrio?
Cambiando la constante de equilibrio
Cambiando la temperatura
d∆G º
o
T − ∆G º
1 ∆G º d ln K p
1 dT
∆G º = −RT ln K o ; ln K o = −
;
=−
p
p
R T
dT
R
T2
d∆G º
∆G º = ∆H º −T∆Sº ;
= −∆Sº
dT
d ln K o
p
dT
=
∆H º
RT 2
d ln K o
p
dT
1 − T∆Sº −∆G º ∆G º +T∆Sº
=−
=
2
R
T
RT 2
Ecuación de van’t Hoff

14. 1901
Primer premio Nobel
de Química
“En reconocimiento a los extraodinarios servicios que ha
prestado con el descubrimiento de las leyes de la dinámica
química y la presión osmótica en disoluciones”.
Jacobus Henricus van’t Hoff
(1852-1911)
[http://www.nobel.se/chemistry/laureates/1901/index.html]
d ln K o
p
dT
∆H º
=
RT 2
K o ( T2 )
p
∫K o ( T1 )
p
∆H º
d ln K = ∫
dT
2
RT
K o (T2 )
p
o
p
T2
T1
∆H º  1 1 
Ecuación integrada ln
 − 
=
o
K p (T1 )
R  T1 T2 
de van’t Hoff


Si
∆Hº = cte

15. K o (T2 )
p
∆H º  1 1 
 − 
ln o
=
K p (T1 )
R  T1 T2 


Consecuencias:
Tomemos T2 > T1
a) Si ∆Hº > 0 (endotérmica)
∆H º
>0
R
1 1
 − >0
T T 
2 
 1
ln
K o (T2 )
p
K o (T1 )
p
> 0 ; K o (T2 ) > K o (T1 )
p
p
T ↑ Kpº ↑
Al aumentar T se favorece la formación de productos.
Se desplaza hacia la derecha.

16. K o (T2 )
p
∆H º  1 1 
 − 
ln o
=
K p (T1 )
R  T1 T2 


Consecuencias:
Tomemos T2 > T1
b) Si ∆Hº < 0 (exotérmica)
∆H º
<0
R
1 1
 − >0
T T 
2 
 1
ln
K o (T2 )
p
K o (T1 )
p
< 0 ; K o (T2 ) < K o (T1 )
p
p
T ↑ Kpº ↓
Al aumentar T se favorece la formación de reactivos.
Se desplaza hacia la izquierda.

17. K o (T2 )
p
Consecuencias:
Tomemos T2 > T1
∆H º  1 1 
 − 
ln o
=
K p (T1 )
R  T1 T2 


c) Si ∆Hº = 0
ln
K o (T2 )
p
K o (T1 )
p
= 0 ; K o (T2 ) = K o (T1 )
p
p
La constante de equilibrio no cambia con T

18. 6
RESPUESTA DEL EQUILIBRIO A UN
CAMBIO DE CONDICIONES.
PRINCIPIO DE LE CHÂTELIER.
¿Cómo podemos modificar la situación de equilibrio?
Cambiando la constante de equilibrio
Cambiando la temperatura
Sin cambiar la constante de equilibrio
Cambiando el resto de condiciones

19. Principio de Le Châtelier
“Si un sistema químico que está en
equilibrio se somete a una perturbación
que cambie cualquiera de las variables
que determina el estado de equilibrio,
el sistema evolucionará para contrarrestar
el efecto de la perturbación”.
Henri Louis Le Châtelier
(1850-1936)

20. 6.1. Efecto de un cambio de temperatura (a P cte)
• Si ∆Hº > 0 (endotérmica): T ↑ ⇒ se desplazará a la derecha
• Si ∆Hº < 0 (exotérmica):
T ↑ ⇒ se desplazará a la izquierda
6.2. Efecto de la adicción/sustracción de moles de
reactivos o productos gaseosos (a T y V ctes)
Kc =
[prod]eq
[reac]eq
[prod]
; Q=
[reac]
• Si agrego productos: Q > Kc ⇒ se desplazará a la izquierda
• Si agrego reactivos: Q < Kc ⇒ se desplazará a la derecha

21. 6.3. Efecto de un cambio de volumen (a T cte)
La disminución de V conlleva que la concentración de total de
moléculas aumente. El sistema tenderá a reducirla.
⇓
Se desplaza hacia donde haya un menor número de moles gaseosos
6.4. Efecto de la presión total (a T cte)
Un aumento de P tiene el mismo efecto que una disminución de V
⇓
Se desplaza hacia donde haya un menor número de moles gaseosos

22. 6.5. Adición de un gas inerte (a T y V ctes)
No altera el equilibrio
[prod] n prod / V
=
[reac] n reac / V
6.6. Adición de un catalizador
No afecta al equilibrio
6.7. Adición de un reactivo/producto sólido o líquido
No altera el equilibrio