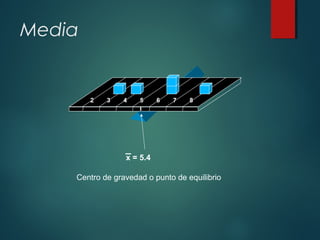
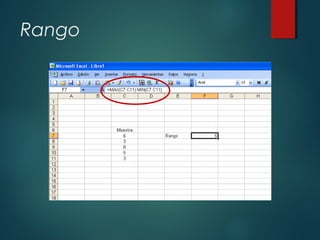
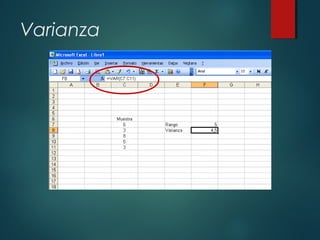
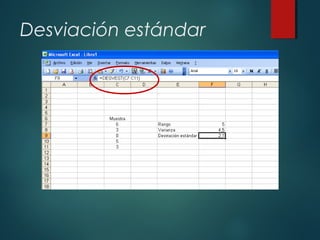
Este documento presenta un resumen de medidas de tendencia central y medidas de dispersión. Explica que las medidas de tendencia central como la media, mediana y moda describen el centro de un conjunto de datos, mientras que las medidas de dispersión como el rango, varianza y desviación estándar miden qué tan dispersos están los datos. Proporciona fórmulas y ejemplos para calcular cada medida. El objetivo es que los estudiantes conozcan y sepan calcular estas medidas estadísticas básicas.

1. Curso de Estadística Básica
Ing. Pablo Jesús Contreras Muñoz
MEDIDAS DE TENDENCIA CENTRAL
Y MEDIDAS DE DISPERSIÓN

2. Objetivo
 Conocer y calcular las medidas de tendencia
central y medidas de dispersión

3. Agenda Sesión 2
• Medidas de tendencia
central
– Media
– Mediana
– Moda
– Media Armónica
– Media Geométrica
• Medidas de dispersión
– Rango
– Varianza
– Desviación
estándar

4. Estadística descriptiva
Medidas de
tendencia
central
Medidas de
dispersión
Medidas de
posición
Tipos de
distribución

5. Medidas de tendencia central
 Son valores numéricos que localizan, de alguna
manera, el centro de un conjunto de datos. El
término promedio a menudo es asociado con
todas las medidas de tendencia central.
•Media
•Mediana
•Moda
•Media Armónica
•Media Geométrica

6. Media
 Se representa por x (se lee como “x barra” o “
media de la muestra”). Es la suma de todos los
valores de la variable x (la suma de valores x se
simboliza como Σx) y dividiendo entre el número
de estos valores, n. Lo anterior se expresa con
una fórmula como:

Media de la muestra: x barra =
suma de x
número
x =
Σx
n

7. Ejemplo
 Un conjunto de datos consta de cinco valores:
6, 3, 8, 6 y 4. Encuentre la media.
 Solución
x =
Σx
n
=
6 + 3 + 8 + 6 + 4
5
=
27
5
= 5.4

8. Media
2 3 4 5 6 7 8
x = 5.4
Centro de gravedad o punto de equilibrio

9. Mediana
 Valor de los datos que ocupa la posición central
cuando los datos se ordenan según su tamaño.
Se representa por x (se lee como “x tilde” o
“mediana de la muestra”).

10. Procedimiento para
encontrar la mediana
1. Ordene los datos
2. Determine la profundidad de la mediana
• La profundidad (número de posiciones a partir de
cualquier extremo), o posición, de la mediana se
determina con la siguiente fórmula:
• La profundidad (o posición) de la mediana se
encuentra al sumar los números de posición de los
valores de los datos más pequeños (1) y más grandes
(n) y dividir el resultado entre 2. (n es el mismo
número que la cantidad de porciones de los datos).
Profundidad de la mediana = número + 1
2
d( x ) = n + 1
2

11. Procedimiento para
encontrar la mediana
3. Determine el valor de la mediana. Contar los
datos ordenados, localizando el dato que está
en la d(x)-ésima posición. La mediana será la
misma sin importar a partir de cuál extremo de
los datos (máximo o mínimo) ordenados se
cuente.

12. Ejemplo
3 5 6 8
3
Me = 5

13. Nota…
• El valor de d(x) es la
profundidad de la mediana, NO
el valor de la mediana, x. Como
se muestra en el anterior
ejemplo, cuando n es impar, la
profundidad de la mediana, d(x),
siempre es un entero. Sin
embargo, cuando n es par, la
profundidad de la mediana, d(x),
siempre es la mitad de un
número entero.

14. Ejemplo Encontrar la mediana de la muestra {9, 6, 7, 9, 10, 8}
1. Los datos, ordenados de manera creciente, son
6, 7, 8, 9, 9, 10
1. Profundidad de la mediana: d(x) = (n+1)/2 = (6+1)/2 = 3.5
2. Es decir, la mediana está a la mitad entre las porciones
de datos tercera y cuarta. Para encontrar el número
situado a la mitad de dos valores cualesquiera, se suman
los dos valores y el resultado se divide entre 2. En este
caso, se suman el tercer valor (8) y el cuarto valor (9),
luego se divide entre 2. La mediana es 8.5. Observe que
de nuevo la mediana separa el conjunto de datos
ordenados en dos subconjuntos del mismo tamaño.
Me = 8.5
6 7 8 9 10
9

15. Moda
 Es el valor de x que ocurre más frecuentemente

16. Nota…
 Las Cinco medidas de tendencia central
representan Cinco métodos distintos para
describir el centro. Estos cuatro valores pueden
ser iguales, aunque es más probable que sean
diferentes. Para los datos muéstrales 6, 7, 8, 9, 9,
10, la media es 8.2, la mediana es 8.5, la moda es
9
6 7 8 9 10
9
8.2 8.5 9

17. Ejercicios
1. Considere la muestra 2, 4, 7, 8, 9. Encuentre:
• La media
• La mediana
• La moda
1. A 15 estudiantes universitarios, elegidos aleatoriamente, se
les solicitó mencionar el número de horas que durmieron la
noche anterior. Los datos resultantes fueron, 5, 6, 6, 8, 7, 7,
9, 5, 4, 8, 11, 6, 7, 8, 7. Encontrar:
• La media
• La mediana
• La moda

18. Ejercicios
 A los reclutas de una academia de policía se les
solicitó presentar un examen que mide la capacidad
que tienen para hacer ejercicio. Esta capacidad
(medida en minutos) se obtuvo para cada uno de los 20
reclutas:
a. Encuentre la media, la mediana, la moda y el rango
medio.
b. Elabore una gráfica de barras para estos datos y
localice la media, la mediana, la moda y el rango medio
sobre la gráfica.
c. Describa la relación que hay entre los cuatro promedios
(semejanza) y qué propiedades muestran los datos por
las que dichos promedios son semejantes
25 27 30 33 30 32 30 34 30 27
26 25 29 31 31 32 34 32 33 30

19. Estadística descriptiva
Medidas de
tendencia
central
Medidas de
dispersión
Medidas de
posición
Tipos de
distribución

20. Medidas de dispersión
 Valores que describen la cantidad de
variabilidad que se encuentra entre los datos:
datos bastante agrupados poseen valores
relativamente pequeños, y datos más dispersos
tienen valores más grandes. El agrupamiento más
estrecho ocurre cuando los datos carecen de
dispersión (ya que todos los datos tienen el
mismo valor), para los cuáles la medida de
dispersión es cero.
 Las medidas de dispersión incluyen:
• Rango
• Varianza
• Desviación Estándar

21. Rango
• Es la diferencia en
valor entre las
porciones de datos
de mayor valor
(Máx) y de menor
valor (Mín):
rango = Máx - Mín

22. Ejemplo
 El rango de la muestra 3, 3, 5, 6, 8 es
 Máx – Mín = 8 – 3 = 5
3 5 6 8
3
Rango
Mín Máx

23. Desviación con respecto a la
media
 Una desviación de la media, x – x, es la
diferencia entre el valor de x y la media x.
x > x Desviación positiva
x < x Desviación negativa
x = x 0

24. Ejemplo
 Considere la muestra 6, 3, 8, 5, 3. Calcular la
desviación con respecto a la media de cada
valor de la muestra.
x =
Σx
n
= 5
Datos
Desviación
x
x - x
6 3 8 5 3
1 -2 3 0 -2

25. Varianza de la muestra
 La varianza de la muestra, s2
, es la media de las
desviaciones al cuadrado, calculada usando
como divisor a n-1.
s2
= Σ(x – x)2
n - 1
Donde n es el tamaño de la muestra, es decir, el número de
datos que hay en la muestra

26. Ejercicio
 Calcular la varianza para la muestra {6, 3, 8, 5, 3}
 Paso 1. Calcula Σx
 Paso 2. Calcula x
 Paso 3. Calcula x – x
 Paso 4. Calcula Σ(x – x)2
 Paso 5. Calcula la varianza

27. Cálculo de la varianza
Paso 1.
Encuentre Σx
Paso 2.
Encuentre
Paso 3.
Encuentre Cada
Paso 4.
Encuentre
Paso 5.
Varianza de la muestra
6 6 - 5 = 1 (1) * (1) = 1
3 3 - 5 = -2 (-2) * (-2) = 4
8 8 - 5 = 3 (3) * (3) = 9
5 5 - 5 = 0 (0) * (0) = 0
3 3 - 5 = -2 (-2) * (-2) = 4
25 5

28. Ejercicio
 Calcular la varianza para la muestra {1, 3, 5, 6, 10}

29. Desviación estándar
2
ss =
• La desviación
estándar de una
muestra, s, es la
raíz cuadrada
positiva de la
varianza:

30. Rango

31. Varianza

32. Desviación estándar

33. Ejercicios
1. Considere la muestra 2, 4, 7, 8, 9. Encuentre:
• Rango
• Varianza
• Desviación estándar
1. Dada la muestra 7, 6, 10, 7, 5, 9, 3, 7, 5, 13.
Encuentre:
• Varianza
• Desviación estándar

34. Ejercicios.
 A los reclutas de una academia de policía se les
solicitó presentar un examen que mide la capacidad
que tienen para hacer ejercicio. Esta capacidad
(medida en minutos) se obtuvo para cada uno de los 20
reclutas:
• Encuentre el rango
• Encuentre la varianza
• Encuentre la desviación estándar
• Use la gráfica de barras que obtuvo en el anterior
ejercicio y trace 1) una recta que represente al rango y
2) una recta que empiece en la media y cuya longitud
represente el valor de la desviación estándar
• Describa cómo están relacionados la distribución de los
datos, el rango y la desviación estándar.
25 27 30 33 30 32 30 34 30 27
26 25 29 31 31 32 34 32 33 30