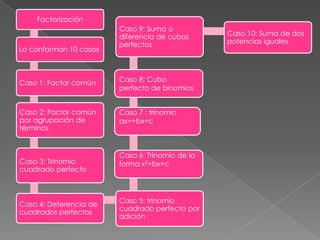
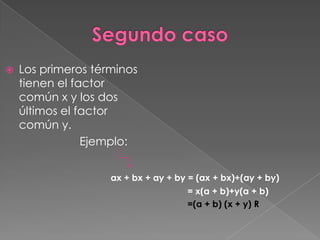
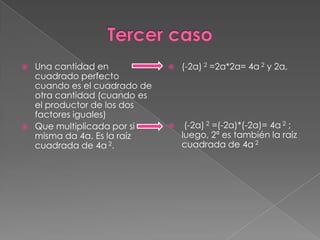
El documento presenta 10 casos de factorización. Estos incluyen factor común, trinomios cuadrados perfectos, diferencia de cuadrados perfectos, y suma o diferencia de cubos perfectos. También explica conceptos como raíces cuadradas, productos notables, y cómo factorizar trinomios de la forma x2 + bx + c.

2. Factorización
Caso 9: Suma o
diferencia de cubos Caso 10: Suma de dos
perfectos potencias iguales
Lo conforman 10 casos
Caso 1: Factor común Caso 8: Cubo
perfecto de binomios
Caso 2: Factor común Caso 7 : trinomio
por agrupación de ax++bx+c
términos
Caso 6: Trinomio de la
Caso 3: Trinomio forma x2+bx+c
cuadrado perfecto
Caso 5: trinomio
Caso 4: Deferencia de
cuadrado perfecto por
cuadrados perfectos
adición

3.  Factor común  Factor común polinomio:
monomio:  Descompone dos
 Se descompone en términos:
factores a2 +2a x(a + b)+m(a + b)
contiene el factor
común a ejemplo:
a²÷2a= a y 2a÷a=2 x(a + b)+m(a + b)= (a + b)(x + m)
a²+2a= a(a+2)

4.  Los primeros términos
tienen el factor
común x y los dos
últimos el factor
común y.
Ejemplo:
ax + bx + ay + by = (ax + bx)+(ay + by)
= x(a + b)+y(a + b)
=(a + b) (x + y) R

5.  Una cantidad en  (-2a) 2 =2a*2a= 4a 2 y 2a,
cuadrado perfecto
cuando es el cuadrado de
otra cantidad (cuando es
el productor de los dos
factores iguales)
 Que multiplicada por si  (-2a) 2 =(-2a)*(-2a)= 4a 2 ;
misma da 4a. Es la raíz luego, 2ª es también la raíz
cuadrada de 4a 2. cuadrada de 4a 2

6.  En los productos  (a + b) (a – b)= a2 - b2
notables se vio que
la suma de dos
cantidades  a2 - b2 = (a + b) (a – b).
multiplicas por su
diferencia es igual al
cuadrado del
minuendo menos el
cuadrado del
sustraendo, o sea

7.  x4 + x2y2 + y4 veamos si  x4 + x2y2 + y4
este es un trinomio + x2y2 - x2y2
cuadrado perfecto. La ____________________________
raíz cuadrada de x4 es x4 + 2x2y2 + y4 - x2y2
x2; la raíz cuadrada de
y4 es y2 y el doble x4+2x2y2+y4 - x2y2 =(x4 + 2x2y2 + y4 )- x2y2
producto de esta raíz es =(x2 + y2)2 - x2y2
2x2y2; luego este =(x2+y2+xy) (x2+y2 -xy)
trinomio ya no es =(x2+xy+y2 ) (x2+xy+y2)R
cuadrado perfecto.

8.  Trinomios de la forma x2 + xb + c  x2 + 5x + 6, m2 + 5m – 14
son trinomios como a2 - 2a -15, y2 - 8y + 15
x2 + 5x + 6 (x ) (x ) 1. Se descompone en 2 binomios,
el primer termino es la raíz
cuadrada de x2 o sea x
x2 + 5x + 6 (x + ) ( x + ) 2. En el primer binomio después
de x se pone el signo + porque
el termino del trinomio tienes
signo +
x2 + 5x + 6 (x + 2) ( x + 3)R 3. Como tenemos signos iguales
se busca dos números cuya
suma sea 5 y cuyo producto
sea 6

9.  Trinomios de esta  Se multiplica el
forma: trinomio por el
coeficiente de x2 que
2x2 + 11x + 5 es 6 y dejando el
3a2 + 7a – 6 producto de 6 por 7x
se tiene:
36x2 – 6(7x) – 8
 Pero 36x2 = (6x)2 y
6(7x)= 7(6x) y luego
pedimos escribir (6x) –
7(6x) – 18.

10.  Para tener una  1 + 12a + 48x2 + 64a2= (1+ 4a)3. R.
expresión algebraica
ordenada con respecto
a una letra debe
cumplir condiciones.
1. Tener cuatro términos.
2. Que el primero y últimos termino sean cubos perfectos.
3. Que el 2° término sea más o menos el triplo del cuadrado del
al raíz cúbica del primer término multiplicado por la raíz
cúbica del último término.

11.  Como en toda división exacta  Regla 1: La suma de sus raíces
el dividendo es igual al cúbicas.
producto del divisor por el
El cuadrado de la primera raíz
cociente, tendremos:
más el producto de las dos
a3 + b3 = (a + b)(a3 – ab + b3) (1) raíces, más el cuadrado de la
a3 – b3 = (a – b)(a3 + ab + b3) (2) segunda raíz.
 Regla 2: La diferencia de sus
raíces cúbicas.
El cuadrado de la primera raíz
más el producto de las dos
raíces, más el cuadrado de la
segunda raíz.

12.  Vemos el modo de hallar el cociente cuando
la división es exacta.
1. an + bn es divisible por a – b siendo n par
o impar.
2. an + bn es divisible por a + b siendo n impar.
3. an – bn es divisible por a – b cuando n es par.
4. an + bn nunca es divisible por a – b.

13. Bibliografía: Algebra de Baldor. Hecho por : Valeria Pillajo