Este documento describe los métodos para fraccionar mezclas multicomponente utilizando múltiples columnas acopladas. Explica que para separar n componentes se requieren n-1 columnas. Presenta nueve configuraciones posibles para sistemas ternarios y discute ventajas y desventajas de cada una. También describe métodos cortos y rigurosos para el cálculo y diseño de sistemas de fraccionamiento multicomponente.

1. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
Generalidades.
En la destilación multicomponente como en mezclas binarias,
los balances de masa y entalpia, y los equilibrios liquido-vapor
se utilizan para el cálculo las etapas de equilibrio. Para cada
componente se escribe un balance de materia aplicado a la
columna en su conjunto o para cada etapa individual, pero solo
hay un balance de energía para toda la columna así como para
cada etapa. Los equilibrios de fases son muchos más complejos
que para mezclas binarias, debido al número de componentes
y a que los equilibrios dependen de la temperatura que varía
de una etapa a otra. En los sistemas binarios la temperatura y
el equilibrio cambian de una etapa a otra, pero (salvo con los
azeótropos) el componente más volátil es más volátil que el
otro componente que pasa a través de la columna. En cambio
en mezclas multicomponente, uno de los componentes puede
ser más volátil que el promedio en una parte de la columna, y
menos volátil que el promedio en otra zona de la columna, lo
que hace que se presenten perfiles de concentraciones muy
complejos (Nabarlazt, D., ).
En destilaciones multicomponente es necesario acentuar que
son necesarios más de un fraccionador para separar en forma
pura los constituyentes de la mezcla original, es decir se
requerirán un total de n – 1 fraccionadores para lograr la
separación completa de un sistema de n componentes
(Treybal, 1980).
Hay muchas formas en las que se pueden acoplar columnas
múltiples con el fin de hacer separaciones de varios
componentes. La elección de la cascada puede tener un gran
efecto sobre los costos de capital y operación. En la Figura 1 se
muestran nueve formas en las que se pueden acoplar las
columnas para un sistema ternario que no forme azeótropos.
Con más componentes, la cantidad de posibilidades aumenta
en forma geométrica. La Figura 1A, muestra la secuencia
directa, donde los componentes más volátiles salen por el
destilado uno a uno. Esta es una de las secuencias más
utilizadas. El esquema B muestra la secuencia indirecta, donde
se separan primero los componentes más pesados y salen uno
a uno por la corriente de fondo. Con más componentes es
posible una gran variedad de combinaciones de estos dos
esquemas. El esquema de la Figura 1C, se parece a la parte A
pero se ha eliminado el vaporizador y una corriente de retorno
de vapor de la segunda columna produce la vaporización a la
primera columna. Se reducen los costos de capital, pero las
columnas están acopladas, lo cual dificulta el control y el
arranque. El esquema D se parece al B, pero una corriente de
líquido de retorno es el reflujo.
El esquema de la Figura 1E usa un enriquecedor lateral,
mientras que el de la parte F usa un agotador lateral, para
purificar el componente intermedio B. La corriente se toma
donde la concentración de B es máxima. Generalmente, estos
esquemas se usan en las refinerías petroleras. La Figura 1G,
muestra un sistema térmicamente acoplado, que a veces se
conoce como columnas Petlyut. La primera columna separa al
componente A de C, que es la separación más sencilla y
después en la segunda columna se obtienen tres productos
puros. Con frecuencia este sistema tiene pocas necesidades
energéticas, pero es más difícil de arrancar y controlar.
Además, este sistema puede necesitar un número excesivo de
etapas, cuando las separaciones A-B o B-C son difíciles. A
veces, se puede tener este esquema en una sola columna de
“pared dividida”. Esta columna de cuatro secciones tiene una
pared vertical entre dos partes de la columna en las dos
secciones intermedias (Figura 2). La alimentación entra en el
lado izquierdo de la pared y las dos secciones en el lado
izquierdo de la pared hacen la misma separación que hace la
primera columna de la figura 1G. En la parte superior de la
pared una mezcla de A y B se divide sobre la pared y entra a las
secciones de rectificación y la intermedia superior. En la parte
inferior de la pared, pasa una mezcla de B y C bajo la pared y
va a las secciones intermedias de agotamiento y de fondos. Así,
las dos secciones intermedias al lado derecho de la pared
hacen la separación que se hace en las dos secciones
intermedias de la segunda columna en la figura 1G. En la Figura
1H se muestra otra variante, donde la separación A-C es tan
fácil que puede usarse un tambor de destilación instantánea
en lugar de la primera columna.
Figura 1. Secuencias de destilación de mezclas ternarias, sin
azeótropos. El componente A es el más volátil y el componente
C es el menos volátil. Fuente: Wankat, P., 2008.
El esquema de la Figura 1I es bastante distinto de los demás,
porque se usa una sola columna con una salida lateral. La salida
lateral no puede ser B totalmente puro, pero si puede tener la
pureza suficiente para cumplir con las especificaciones del
producto. Este esquema y otros muy parecidos, se usan con
mucha frecuencia cuando la concentración de C en la

2. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
alimentación es muy baja. Entonces en el punto de máxima
concentración de B no habrá mucho C presente. También
pueden usar métodos con salidas laterales, que se conectan a
otras columnas y para separaciones de cuatro componentes.
Figura III.2 Columna de Pared dividida. Fuente:
http://www.dcne.ugto.mx/Contenido/revista/numeros/17/d
estilacion.htm
El mejor método a usar depende de la complejidad de la
separación. La facilidad de las diversas separaciones, las
purezas necesarias y las concentraciones de la alimentación
son importantes para determinar la configuración óptima. Esta
configuración óptima también puede depender de cómo se
define “lo mejor”. Una forma de estar seguro de haber
encontrado el mejor método es modelar todos los sistemas y
hacer pruebas con ellos. Con frecuencia se utilizan métodos
abreviados de cálculo, para ahorrar tiempo y costo de
cómputo (Wankat, P., 2008).
Un método alternativo para el diseño es aplicar las reglas
heurísticas o reglas empíricas, que consiste en reglas fáciles
para excluir muchos de los sistemas posibles. Se ha
desarrollado la heurística haciendo una gran cantidad de
simulaciones, para después buscar conceptos que relacionen
los mejores esquemas. Algunas de las heurísticas más
comunes, citadas en orden de importancia incluyen (Wankat,
P., 2008):
1. Separar primero los componentes peligrosos, corrosivos y
reactivos. Se reduce al mínimo los riegos de seguridad,
sacará los compuestos inestables y reducirá la necesidad de
usar materiales de construcción costosos en columnas
posteriores.
2. No usar destilación si αLK,HK < αmin, si αmin ̴ 1,05 a 1,10.
Elimina la necesidad de columnas costosas
3. Separar primero los componentes que requieran
temperaturas muy altas o muy bajas. Mantendrá bajos
costos.
4. Hacer primero los cortes fáciles (α grandes). Cuando hay
varios componentes y los flujos de alimentación son
grandes.
5. La siguiente fracción debe eliminar los componentes en
exceso. Sugiere reducir las tasas de alimentación lo más
rápido que sea posible.
6. La siguiente fracción debe sacar el componente más volátil.
Se eliminan los materiales difíciles de condensar, es
probable que se consigan reducciones en las presiones de
la columna.
7. Hacer las separaciones difíciles como separaciones
binarias. Hace que se tenga la mínima tasa de alimentación
y en consecuencia el diámetro mínimo de la columna
necesario para separaciones difíciles.
8. Favorecer los fraccionamientos 50:50. Balancea la columna
de tal modo que no cambien los flujos en forma drástica.
9. Si es posible, las eliminaciones de productos finales deben
ser como productos destilados.
Dos heurísticas adicionales que no aparecen en orden de
importancia, pero que pueden forzar al diseñador para buscar
secuencias adicionales son:
• Tener en cuenta salidas laterales para separaciones difíciles
• Tener en cuenta columnas térmicamente acopladas y de
varios efectos, en especial si la energía es costosa.
Ejercicio 1. Secuencia de columnas con heurísticas.
Se debe destilar una alimentación con 25% mol de etanol, 15%
mol de isopropanol, 35% mol de n-propanol, 10% mol de
isobutanol y 15% mol de n-butanol. Se desea obtener cada
alcohol con 98% de pureza. Determinar las configuraciones
óptimas de las columnas.
Solución:
Los datos de equilibrio se pueden aproximar como
volatilidades relativas constantes (King, 1981), con n-propanol
como componente de referencia:
Componente Fracción molar αi,n-P
Etanol (E) 0,25 2,09
Isopropanol (i-P) 0,15 1,82
n-Propanol (n-P) 0,35 1,0
Isobutanol (i-B) 0,10 0,677
n-Butanol (n-B) 0,15 0,428
Para aplicar las heurísticas es conveniente determinar las
volatilidades relativas de todos los pares adyacentes de
compuestos y así observar su facilidad o dificultad de
separación.
,
,
1,15
,
,
1,82
1,00
0,677
1,48
0,677
0,428
1,58
Las cuatro primeras heurísticas se pueden ignorar ya que no
hay presencia de componentes peligrosos, corrosivos ni
reactivos y la volatilidad relativa de los pares adyacentes son
cercanas, es decir no hay mucha dificultad o facilidad de
separación entre ellos.

3. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
Caso 1: tomando en cuenta las heurísticas 6 y 9 se obtiene la
secuencia directa.
Caso 2: Basada en la heurística 8, fraccionamiento 50:50, en la
columna A y a su vez tomando la heurística 7 para la selección
de los componentes que saldrán por cada corriente así, por la
corriente de tope sale Etanol e isopropanol y por la corriente
de fondo sale n-propanol, i-butanol y n-butanol. Para la
columna C, las heurísticas 5 y 8, como se observa en la figura
siguiente.
Caso 3. Utilizando las heurísticas 7, 8 y 11 se obtiene una
modificación del caso 2.
Métodos de cálculo.
El fraccionamiento de mezclas multicomponente se basa en los
mismos principios de equilibrio de fases que la de mezclas
binarias. El diseño o análisis de las columnas de
fraccionamiento de mezclas multicomponente utiliza
relaciones de equilibrio y balances de masa y energía (Foust y
col., 1998).
Para el fraccionamiento de mezclas con “n” componentes, n >
2, es difícil obtener una solución analítica y no son aplicables
los métodos gráficos, y deben hacerse una serie de asunciones
sobre la distribución de los componentes de la alimentación en
el destilado y en el producto de fondo.
Para su diseño y análisis se dispone de los métodos cortos,
rigurosos. El cálculo riguroso es extremadamente complejo e
involucra métodos prolongados al tanteo y las computadoras
de alta velocidad se emplean con mucha frecuencia (Treybal,
R., 1980).
Métodos cortos.
Los métodos cortos son diseños preliminares, estudios
paramétricos para establecer condiciones óptimas de procesos
y síntesis de procesos, con el objeto de determinar la secuencia
óptima de separación. En la práctica son usados como diseño
preliminar y representan el punto de partida para los métodos
rigurosos.
Son útiles para hidrocarburos u otros sistemas con valores de
K disponibles o fácilmente calculables, no se aplican a sistemas
cuyas volatilidades cercanas a la unidad o que varían muy
ampliamente, con azeótropos, reacciones descomposiciones,
etc.
Sin embargo, el método corto no funciona para todos los
sistemas. Para sistemas altamente no ideales, los métodos
cortos pueden dar resultados erróneos o ningún resultado. En
particular, para columnas en las que las volatilidades relativas
varían, los métodos cortos darán resultados deficientes, ya que
tanto el método de Fenske como el de Underwood suponen
que se puede usar una volatilidad relativa promedio para los
cálculos de cada componente.
Estos métodos se pueden aplicar fácilmente por medio de
cálculos manuales si las propiedades físicas son
independientes de la composición, caso contario se
recomienda utilizar los métodos rigurosos.
Entre los métodos aproximados se mencionan (Holland, Ch.,
2000):
1. Método de Edmister
Para separaciones en las que intervienen cascadas en
contracorriente con alimentaciones intermedias, tales
como destilación.
2. Método de Kremser y sus variantes,
Para separaciones en las que intervienen varias
cascadas simples en contracorriente, tales como
absorción, agotamiento y extracción liquido – líquido
3. Método sistema seudo binario: Método de Hengstebeck’s
Cambia el sistema multicomponente a sistema binario.
Utiliza las ecuaciones de McCabe-Thiele y las relaciones
de equilibrio.
3. Método de Fenske – Underwood – Gilliland y sus variantes,
Para determinar el reflujo y las etapas necesarias en la
destilación de sistemas multicomponente.
Métodos rigurosos.
Un método riguroso describe la columna como un conjunto de
ecuaciones y su solución permite obtener las condiciones de
operación de la columna. Todos los flujos son expresados en
moles/h. También, cuando los cálculos rigurosos son
desarrollados se debe especificar lo siguiente:

4. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
• Flujo, composición y condición de cada alimentación.
• Número de etapas en la columna
• La etapa para cada alimentación, producto,
intercambiadores de calor y pumparound
(intercambiadores o rehervidores intermedios).
• Especificaciones de la separación
• La optimización de la separación.
El diseño y los cálculos de la columna y los cálculos se
presentan en estado estacionario es decir,
∑ !" #$ ! ! % $&'!(%ó&* ∑ !" #$ +" # (' *
∑ $ #$ ( ! , %$" ( + &$&'$ $& ! ! % $&'!(% &$ *
∑ $ #$ ( + &$&'$ $& ! ( ""%$&'$ #$ +" # (' *
$&'! +%! #$ ! ! % $&'!(%ó& + (! " !#%(% &!# $&'! +%! #$ +" # (' +
(! " "$ .%#
Kister (1992) indica que Friday y Smith (1964) y King (1980) han
dividido los métodos rigurosos en cuatro clases básica:
• El método de punto de burbuja (BP)
• El método de la suma de flujos (SR)
• El método de Newton 2N
• El método de Newton global o corrección simultanea (SC)
El método original de Wang y Henke (1966) dio el nombre al
método de punto de burbuja porque las temperaturas en las
etapas son calculadas aplicando la ecuación de punto de
burbuja. Este método se recomienda cuando la alimentación
está constituida por constituyentes de volatilidad parecida. El
método SR usa los balances de energía para actualizar las
temperaturas de las etapas y se recomienda cuando la
alimentación está constituida por constituyentes de muy
diferente solubilidad o volatilidad (puntos de ebullición
alejados). El método 2N Newton calcula la temperatura y los
flujos totales juntos pero las composiciones se calculan
separadas, dependiendo de la etapa. El método 2N permite
una considerable flexibilidad en la elección de las variables
especificadas y, por lo general, es capaz de resolver todos los
problemas. Estos tres métodos se denominan métodos de
separación o desacoplamiento de ecuaciones porque las
ecuaciones MESH se dividen y agrupan o se dividen y
emparejan con variables MESH para ser resueltas en una serie
de pasos. El método SC intenta resolver todas las ecuaciones y
variables MESH juntas.
Es importante mencionar que las ecuaciones MESH son todas
las ecuaciones que se usan para describir la operación de una
columna de destilación en estado estacionario. Estas
ecuaciones definen los balances externos de la columna:
balances de materia global, balances de energía y las
composiciones de los productos. En la parte interna de la
columna describen las condiciones de equilibrio (etapa a
etapa) balances de materia global y por componente y
balances de energía. Las variables independientes de una
columna son las velocidades de flujo y composiciones de los
productos, los flujos internos de la columna y sus
composiciones y la temperatura en la etapa. Las constantes de
equilibrio, valores de K, y las entalpias de mezclas son variable
dependiente. Se asume que cada etapa esta en equilibrio (es
una etapa teórica), aunque puede aplicarse una eficiencia en
las ecuaciones.
Así, los métodos rigurosos convierten a una columna en un
grupo de variable y ecuaciones. Las variables MESH son
frecuentemente referidas a un estado variable y ellas son:
• Temperatura de etapas, Tj
• Flujos internos de líquido y vapor, Vj y Lj
• Composiciones de los componentes de líquido y vapor en
cada etapa, yij y xij o los flujos individuales en cada etapa,
Vij y Lij.
Dónde: i es el número de componente y j es el número de
etapas.
Otros métodos adicionales son:
• El método inside-out
• El método de relajación
• El método continuación-homotopia
• El método de no-equilibrio
Los métodos de relajación, inside-out y homotopia-
continuación son extensiones o parte de los primeros cuatro
métodos que permiten dar solución a sistemas difíciles. El
modelo de no-equilibrio se basa en velocidades o fenómenos
de transporte y el concepto de etapa ideal y cualquier uso de
eficiencias. Son más adecuados para columnas donde las
etapas teóricas son difíciles de definir y las eficiencias son
difíciles de predecir o aplicar.
Por lo general, el análisis de mezclas multicomponente se hace
inicialmente utilizando métodos cortos, para un diseño
preliminar y luego se hace un diseño más complejo donde se
hace un diseño detallado plato a plato. En este método sencillo
supone platos ideales en el diseño y luego corrige el número
de etapas con la eficiencia de plato. Las condiciones limitantes
del proceso, reflujo total (número mínimo de etapas) y reflujo
mínimo se utilizan para validar el diseño.
En la destilación de varios componentes no se especifican por
completo las composiciones del destilado ni de los fondos, ya
que no se dispone de suficientes variables para hacerlo. Esto
ocasiona un efecto importante en el procedimiento de cálculo.
Y de acuerdo a las especificaciones que se tengan de la
separación deseada, bien sea por flujos, composiciones o
recuperaciones fraccionarias de algunos componentes en las
corrientes de tope y de fondo, se puede identificar a los
componentes clave, clave liviano, clave pesado, componentes
no clave.
Componentes Clave: pueden ser o no aquellos cuyas
separaciones se han especificado, en ellos se basa la
separación de los productos.
Componente Clave Liviano (LK, Light Key o CL, Clave Liviano):
Es el componente más pesado entre los componentes livianos.
Es el componente de mayor volatilidad entre los compuestos

5. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
que salen por el fondo y se encuentra en una cantidad
considerable (menor al 2%).
Componente Clave Pesado (HK, Heavy Key o CP, Clave Pesado):
Es el componente más liviano entre los componentes pesados.
Es el componente de menor volatilidad relativa entre los
compuestos que salen por el destilado y se encuentra en una
cantidad considerable (menor al 2%).
Componente no Clave Distribuido (DNK, Distributed Non Key o
NCD, No Clave Distribuido): Es aquel o aquellos componentes
que poseen volatilidad relativa intermedia entre los
componentes clave liviano y pesado o esta cercanamente igual
a la volatilidad de uno de los componentes clave.
Componente no clave liviano (LNK, Light Non Key o NCL, No
Clave Liviano): es el componente más liviano que el
componente clave liviano
Componente no clave pesado (HNK, Heavy Non Key o NCP, No
Clave Pesado): es el componente más pesado que el
componente clave pesado.
Componente de referencia: el componente clave pesado es el
componente de referencia, se debe conocer el flujo de tope y
fondo.
Componentes clave adyacentes: son los componentes clave
cuyas volatilidades relativas son continuas
Componentes clave no adyacentes: son aquellos componentes
clave que poseen uno o más componentes no clave con
volatilidad intermedia entre ellos o volatilidad cercana a uno
de los clave.
Especificación del producto deseado para identificar los
constituyentes.
La especificación de la separación varía considerablemente en
su formulación de acuerdo al uso final del producto y la
naturaleza de la alimentación.
a. Expresiones de especificación
En la Figura 3, se muestran los diferentes constituyentes de
la alimentación de la columna de tope a fondo en orden de
volatilidad decreciente. El área que ellos ocupan es
proporcional a su concentración en la alimentación.
b. El rectángulo en si representa el flujo total de alimentación
y el área ocupada por cada uno de los constituyentes
representa los flujos individuales en la alimentación.
c. Los constituyentes son denotados por letras desde la “a”
hasta la “g” y la separación marca la frontera de los
constituyentes livianos y pesados con respecto a la
destilación bajo consideración.
d. Para el caso mostrado e la Figura, la separación está situada
entre los constituyentes "d" y "e". Esto permite determinar
la naturaleza de los constituyentes ligeros desde “a” hasta
“d” los cuales se encuentran principalmente en el
destilado, y la naturaleza de los constituyentes pesados
desde “e” hasta “g” los cuales se encuentran
principalmente en el producto de fondo.
Figura 3 Esquema de la separación ideal. Fuente: Tomado FRI,
2002.
e. Esta separación puede definirse como una serie de
separaciones, donde cada componente ligero “a”, “b”, “c”
y “d”, pueden separarse individualmente de cada uno de
los componentes pesados “e”, “f” y “g”.
f. De estas numerosas separaciones binarias, la más difícil
será aquella donde sus dos componentes tengan una
volatilidad cercana con respecto a la frontera de interés. En
virtud de su importancia estos constituyentes se les conoce
como componentes clave.
De modo que, el componente clave ligero es el
constituyente “d”; Y el componente clave pesado es el
constituyente “e”. Identificados los constituyentes clave es
posible especificar la separación limitando la cantidad del
clase ligero y el clave pesado en el destilado y en el residuo,
respectivamente.
g. En el caso de columnas de destilación simple, dos
productos, la separación deseada está completamente
definida donde estos dos productos están especificados.
Estas especificaciones pueden estar especificadas en
términos de pureza o rendimiento y las ecuaciones pueden
ser escritas bajo la siguiente notación,
Rendimiento del clave liviano en el destilado: este valor
expresa el mínimo porcentaje a recuperar del clave liviano
en el destilado.
%0$( + 12
345
645
3∗89,45
6∗8:,45
Rendimiento del clave pesado en el residuo: igualmente es
el mínimo porcentaje a recuperar del clave pesado en el
producto de fondo.
%0$( + ;2 <5
6<5
∗ 8=,<5
6∗ 8:,<5
Concentración límite de los constituyentes clave pesados (e
a g) en el destilado, k: expresa la máxima fracción molar de
los constituyentes clave pesados en el destilado.
∑ 3>
>?@
>?A
∑ 3>
>?@
>?B
∑ 3>
>?@
>?A
3
C D ∑ E ,3 C D
FG
FH
Concentración límite de los constituyentes clave ligero (a
hasta d) en el producto de fondo: l es la fracción molar
máxima del constituyente ligero en el producto e fondo.
∑ >
>?I
>?B
∑ >
>?@
>?B
∑ >
>?I
>?B
C ℓ ∑ E , C ℓ
FK
F L

6. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
En consecuencia, una vez elegido los componentes clave el
diseñador asigna arbitrariamente valores bajos para xHK en el
destilado y para xLK en el producto de fondo. La elección de
valores bajos para el xHK,D y xLK,B, quiere decir que la mayor
parte del clave liviano sale por el destilado y la mayor parte del
clave pesado sale por la corriente de fondo. Los componentes
más ligeros que el clave liviano solo saldrán por la corriente de
destilado; igualmente los componentes más pesados que el
clave pesado solo salen por la corriente de fondo. En este caso
se dice que los componentes son “no distribuidos” mientras
que el clave liviano y el clave pesado siempre están
“distribuidos”, porque ambos se encuentran en forma
apreciable en ambas corrientes de producto.
Contrariamente en mezclas binarias, la elección de dos
componentes clave no determina los balances de masa, puesto
que no todas las fracciones mol se pueden calcular
exclusivamente por balances de materia y se requieren
cálculos de equilibrio para determinar las concentraciones del
vapor a la temperatura de rocío a partir del plato superior, y
del líquido a la temperatura de burbuja que sale del
rehervidor.
Al identificar los componentes clave se puede hacer la
distribución aproximada de los componentes en la corriente de
tope y de fondo. Si se requiere una separación nítida ninguno
de los componentes alimentados se distribuyen es decir, el
componente clave liviano y los componentes más livianos que
el clave liviano salen por la corriente de tope y el componente
clave pesado y los componentes más pesados que el clave
pesado salen por la corriente de fondo, como se observa en la
Figura 3, sería la separación deseada o ideal.
La hipótesis obvia es que todos los componentes no clave
liviano salen por el tope y todos los componentes no clave
pesados salen por la corriente de fondo. Sin embargo, en una
separación real se observa que una pequeña cantidad de un
componente no clave pesado puede ser separado y salir por la
corriente de tope, como se observa en la Figura 4. En las
separaciones reales se delimita el punto de corte y la línea de
separación.
El punto de corte es la frontera entre los componentes que
salen por la corriente de tope y la corriente de fondo y la línea
de separación refleja la separación real realizada. La
composición real del destilado y el producto de fondo está
representada por la línea curva determinando igual áreas de
cada lado de la línea horizontal del punto de corte. Así, el
destilado estará localizado sobre la línea de separación y el
producto de fondo bajo la línea de separación. En la figura 4 se
observa que los componentes a, b, c, y g no se separan, y los
componentes a, b y c solo están presentes en el destilado
(componentes más livianos que el clave liviano) y g solo
aparece en la corriente de fondo.
Figura 4. Esquema de la separación real. Fuente: Tomado de
FRI, 2009.
Especificación del producto deseado y separación de cortes
de petróleo.
La alimentación a procesar es una mezcla de constituyentes
desconocidos o una mezcla compleja. Esta consiste
principalmente de cortes de petróleo o craqueados o petróleo
crudo. Y están especificados mediante:
• Un punto de corte que indica la temperatura de ebullición,
que es la frontera teórica entre los cortes.
• Los requerimientos de calidad del fraccionamiento está
relacionado a la posición relativa en la curva de destilación
ASTM de los dos productos.
1. Punto de corte TBP
Este punto determina el balance de materia global de la
columna de una manera simple, es decir, las proporciones
de D y B en el caso de una columna de dos productos, como
se muestra en la Figura 5.
Figura 5. Balances de materia sobre la curva TBP
Estas curvas TBP, por lo general, vienen expresadas en
masa o volumen, pero también pueden ser utilizadas para
establecer la curva molar TBP de modo que se pueda
realizar el balance de materia en moles.
Es importante mencionar que este principio es aplicable a
columnas complejas con extracciones múltiples.
2. Calidad de la separación perfecta.
La calidad de la separación es identificada por la posición
relativa de los cortes en la curva de destilación ASTM.
Si “t” es el punto de corte, el corte liviano no contiene
ningún componente con punto de ebullición más alto que
“t”. Igualmente, el corte pesado solo contiene
constituyentes con punto de ebullición más altos que “t”,

7. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
como se muestra en la Figura 6a. En la Figura 6b, se
muestra que el punto final del corte ligero de la curva ASTM
es marcadamente más bajo que “t” y el punto final del
corte pesado de la curva ASTM es mucho más alto que “t”.
Figura 6. Esquema de la posición relativa de cortes en la
curva de destilación ASTM en una separación ideal.
3. Separación real.
En una separación real aparecen los constituyentes con
puntos de ebullición que “t” en el producto liviano e
igualmente estarán presentes constituyentes con puntos
de ebullición más altos que “t” en el producto pesado,
como se observa en la Figura 7a.
Figura 7. Esquema de posición relativa de cortes en la curva
de destilación ASTM en una separación real.
Por tanto, la última parte del corte ligero de la curva ASTM
está en la zona de temperatura más alta y por el contrario,
la parte inicial del corte pesado de la curva ASTM está en la
zona de temperatura más baja, como se observa en la
Figura 7b. Igualmente, se observa un pequeño diferencial
de temperatura, ∆T, entre las dos curvas y su valor es una
función de la calidad de la separación.
En consecuencia, este es una forma para caracterizar el
fraccionamiento y puede expresarse como sigue,
∆N 'O% PQRSH THULKQ − ' O% PQRSH W X L Q
Esta relación entre las temperaturas de destilación ASTM a
95% en volumen y 5% en volumen de fracciones
adyacentes ligeras y pesadas, respectivamente, definen
una buena separación. Es decir:
Si ∆T > 0, llamada ASTM gap (buena separación)
Si ∆T < 0, llamada ASTM overlap (mala separación).
Parámetros de diseño en una columna de destilación.
Entre los parámetros más importantes para el diseño de una
columna de destilación se mencionan:
• Presión de operación
• Temperatura del destilado y del residuo
• Caudales molares del destilado y del residuo
• Composición del destilado y del residuo
• Especificación de la pureza para cada uno de los
componentes
• Número mínimo de etapas (utilizando una relación de
reflujo total)
• Relaciones de reflujo mínimo y de operación.
• Número de etapas teóricas y ubicación del plato de
alimentación
• Caudales internos de líquido y vapor
• Eficiencia global de la torre
• Número de platos reales y ubicación real del plato de
alimentación
• Diámetro de la columna
• Altura total de la torre
• Calores intercambiados en el condensador y en el
rehervidor.
Presión de operación y tipo de condensador.
Una columna de destilación puede trabajar a presión,
atmosférica, presión de vacío y presión superatmosférica. Lo
más económico sería trabajar a presión atmosférica, pero no
siempre es posible.
Las columnas de destilación trabajan a vacío si la temperatura
produce descomposición de los componentes, ensuciamiento
o polimerización y si las elevadas temperaturas en el hervidor
complica el aporte de calor; y operan a altas presiones en el
caso en que resulte interesante refrigerar con agua o con aire
en el condensador. De manera general, a altas presiones la
separación se hace más difícil (punto crítico y = x, y no hay
separación). A la inversa, a medida que la presión disminuye
la separación se hace más fácil y se requieren menos platos.
En general, la presión se fija por una o más consideraciones. En
caso de operar a sobrepresión, se debe elegir la menor presión
posible ya que el aumento de la presión produce una
disminución de la volatilidad y dificulta la separación. Si se
trabaja a vacío debe preferir operar a la mayor presión posible,
ya que a medida que aumenta el vacío incrementa el volumen

8. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
del vapor y se requieren columnas de mayor diámetro y por
tanto los costos son altos.
Otro factor a considerar es la presión del punto de burbuja y
de rocío en el tope de la columna y el tipo de refrigerante
empleado en los condensadores. La estabilidad térmica de los
componentes que se destilan es importante al momento de
fijar la presión de la columna, así para evitar la polimerización
de un producto se puede considerar la reducción de la presión
de una columna. Finalmente se debe analizar la posibilidad de
desplazar un azeótropo trabajando a más de una presión
Pressure Swing Distillation.
La presión de operación es determinada por las condiciones
que aumentan la condensación en el condensador o en el
tambor de destilado; tomando como presión de referencia la
presión de vapor o la presión de burbuja del destilado
(Temperatura y composición del destilado). En la selección de
la presión de la columna se deben tomar en cuenta dos
restricciones principales, relacionadas con la temperatura del
tambor de reflujo y la temperatura en el fondo de la columna
(Ver Figura 8).
Figura 8. Esquema parte superior de columna.
Dependiendo de la transferencia de calor en el condensador,
la temperatura en el tambor de reflujo, tb, es al menor unos
pocos grados más alta que la temperatura del fluido frio a la
entrada, tCF. Se prefiere trabajar a presiones bajas, y
consecuentemente requiere que la temperatura del tambor de
reflujo sea lo más baja posible.
La temperatura en el tambor de destilado depende
principalmente de la temperatura del fluido de enfriamiento
utilizado en el condensador, y la composición del destilado
depende de la naturaleza de la mezcla a procesar, las
especificaciones de la separación y del correspondiente
balance de materia. El fluido de enfriamiento a utilizar puede
ser aire, agua, un refrigerante (propileno, etileno, freón, etc.)
o cualquier otro fluido disponible a una temperatura
suficientemente baja. Si se emplea un enfriador atmosférico se
debe usar un acercamiento de 15 °C, respecto a la temperatura
del aire; este valor es considerado satisfactorio en cuanto a
que no resulta excesivo para un área de intercambio de calor.
Obviamente esta temperatura del aire puede ser mucho más
alta si es necesario. Como en el caso del fraccionamiento de
algunos cortes de petróleo, la separación de aromáticos, para
los cuales una excesiva baja temperatura en el tambor de
reflujo, implica operar a condiciones de vacío. Resulta más
económico trabajar a presiones por encima de la atmosférica
(unos pocos mbar) para mantener el tambor de reflujo a una
temperatura más alta.
Si se emplea agua de enfriamiento se recomienda usar un
acercamiento de 10 °C, respecto a la temperatura de ingreso
del agua. Al igual que en el enfriador por aire este
acercamiento puede modificarse para unas condiciones
específicas y debe ser económicamente justificado. En el caso,
de utilizar un refrigerante se debe usar un acercamiento
aproximado de 5 °C, respecto a la temperatura del
refrigerante. Las mínimas temperaturas que son utilizadas en
la industria con refrigerantes son equivalentes a su
temperatura de ebullición a una presión ligeramente por
encima de la atmosférica. Esto corresponde a las condiciones
de presión mínima de entrada del refrigerante al ciclo del
comprensor. Con etileno (punto de ebullición = 104 ᵒC) una
temperatura de -100 ᵒC se puede alcanzar, con propileno
(punto de ebullición = -48 ᵒC): -40 ᵒC a – 45 ᵒC, con amonio
(punto de ebullición = -33 ᵒC): -30 ᵒC, etc. (IFP, 1999).
Un estimado inicial de la presión de operación y el tipo de
condensador (total o parcial) se obtiene siguiendo el algoritmo
presentado por Henley & Seader (1998), mostrado en la Figura
9. Este procedimiento se ha formulado para alcanzar una
presión PD en el tambor de reflujo comprendida entre 0 y 415
psia (2,86 MPa) para una temperatura mínima de 120 °F (49
°C) utilizando agua como fluido de enfriamiento en el
condensador. Se supone que las caídas de presión en la
columna y en el condensador son de 5 psia. La caída de presión
debido a los platos es la suma de las caídas de presión causada
cuando el vapor se eleva a través de cada plato. En condiciones
normales, el rango de valores de caídas de presión en los platos
es de 3 a 20 mbar en cada plato real. Una caída de presión de
3 mbar ocurre para un tamaño específico de plato, de 6 a 10
mbar son los valores más comunes, y valores sobre los 15 mbar
pueden ser considerados altos. Usualmente, en columnas de
20 a 50 platos reales, la presión en el rehervidor deberá ser de
0,1 a 0,5 mbar más alta que en el tope de la columna. Esta es
una variación muy ligera para columnas que operan bajo
presión, pero es muy significativa en columnas que operan a
vacío. Por tanto, la temperatura en el fondo de la columna no
debe dar lugar a descomposición del producto de colas, ni
estar próxima a las condiciones críticas.
En general, la metodología a seguir para estimar la presión de
la columna y el tipo de condensador se indica a continuación:
1. Se realiza el balance de materia preliminar en la columna
de destilación para estimar las composiciones y flujos de las
corrientes de tope y fondo de la columna.
2. Se asume condensador total y como fluido de enfriamiento
agua, por tanto la temperatura en el tambor de destilado
es 120 °F. Bajo estas condiciones se calcula la presión de
burbuja en la corriente de destilado, PD,CALCULADA.
a. Si PD,CALCULADA < 215 psia, use un condensador total a
menos que requiera vapor en el destilado en cuyo caso

9. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
use un condensador parcial. Si PD,CALCULADA < 30 psia,
ajuste la presión a 30 psia y evite la operación cercana
a vacío.
NOTA: Si la temperatura critica de los componentes de
la corriente de destilado es menor a 120 °F (Tci < 120 °F),
la presión es alta y probablemente el condensador es
parcial.
Figura 9. Algoritmo para establecer la presión de la columna y
el tipo de condensador. Fuente: Tomado de Henley, E. J. y
Seader, J. D. (1998).
b. Si la presión de burbuja en el destilado es mayor a 215
psia pero menor a 365 psia (215 psia < PD,CALCULADA <
365), use un condensador parcial y calcule la presión de
rocío a 120 °F en la corriente de destilado, PD.
c. Si PDCALCULADA > 365 psia, opere el condensador parcial a
415 psia con un adecuado refrigerante.
El procedimiento para determinar la temperatura (o
presión) de burbuja o rocío es definiendo los valores de
K (constante de equilibrio) como la relación de
equilibrio entre las fase liquida y vapor para una
determinada especie química.
2
Y>
8>
>Z
T>
[,>
Z
[,>
% & !+ %(!] $ ! $^$ #$ 0! ' ^ _! ' & *
Estos valores son una medida de la tendencia a
concentrarse una especie en la fase de vapor. Cuando
el valor de K es mayor a la unidad, dicha especie se
concentra en la fase de vapor, cuando el valor de K es
menor a la unidad dicha especie tiende a concentrarse
en la fase liquida y se considera como un componente
pesado.
Cuando se consideran ambas fases, vapor y líquido,
soluciones ideales, se reducen las expresiones de K a
ecuaciones que contienen solo propiedades de la
especie pura y por tanto expresan los valores de K como
funciones de la temperatura y presión, independientes
de las composiciones de las fases. Sin embargo, el
método está limitado para cualquier especie a
temperaturas subcriticas, porque la curva de presión de
vapor termina en el punto crítico.
También, se encuentran en la literatura los
nomogramas de DePriester, en los cuales se obtienen
los valores de K de los hidrocarburos más livianos. En
estos nomogramas se obtiene los valores de K en
función de la temperatura y presión. Sin embargo, solo
son adecuados para cálculos aproximados, ya que se
basan en un efecto promedio de la composición.
Para el cálculo de la temperatura de burbuja, la
ecuación básica es:
∑ ^ ∑ E ∗ 2 1,0000
Para el cálculo de la temperatura de rocío, la ecuación
básica es:
∑ E ∑ ^
2
Z 1,0000
3. Para elegir la presión en el condensador, adicione 10 psia
para estimar la presión de fondo (PB), Ludwing (1998) indica
que debe adicionarse de 10 a 15 psi; con esta presión de
fondo se calcula la temperatura de burbuja, TB (Ver Figura
10). Si esta temperatura excede la temperatura de
descomposición o temperatura critica de los componentes
de fondo, se disminuye apropiadamente la presión en el
destilado, PD, y se determina nuevamente la TB y se
compara nuevamente con la TCi,B (TB < TCi,B).
4. La presión de la columna se estima mediante el promedio
aritmético de las presiones de tope y fondo de la columna.
5. La condición termodinámica de la alimentación se
determina mediante la aplicación de un flash adiabático
para una presión del plato de alimentación de PD + 7,5 psia.
`
Ea 1 − 2 *
1 + b 2 − 1*
0 b
c
d
F
Figura 10. Esquema de la columna para la estimación de la
presión de fondo. Fuente: FRI, 2002.
Normalmente se considera que el reflujo que se devuelve a la
columna es un líquido saturado. Esto será así cuando el
condensador sea parcial o mixto, pero cuando se trata de un
condensador total, el reflujo puede y suele ser un líquido
subenfriado. Si el reflujo es un líquido subenfriado, al entrar en
la columna aumenta de temperatura y provoca la
condensación de parte del vapor, de forma que la entalpía de
condensación del vapor proporciona el calor sensible
necesario para calentar el reflujo subenfriado hasta su
temperatura de burbuja. En estas circunstancias, el reflujo
interno es mayor que el reflujo externo que se devuelve desde

10. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
el tambor de reflujo. La relación de reflujo interno se
calcularía como el producto del reflujo externo por
(1+CpLΔTsubenfriamiento/ΔHvap); donde CpLΔTsubenfriamiento representa
el calor sensible necesario para calentar el reflujo y tanto
CpL como ΔHvap están referidos a 1 mol de mezcla (Henley, E. J.,
Seader, J. D. y Roper, K. 2011).
La presión es controlada por la contrapresión del tambor de
reflujo:
• 0,2 – 0,34 barg ( 3 – 5 psig)
• La presión de la zona flash es usualmente 0,34 – 0,54 bar
más alta que la presión del plato de tope.
La temperatura de tope de la columna debe ser 14 -17 °C más
alta que la temperatura de rocío del agua a la presión de tope
de la columna.
Otros criterios que influyen en la selección de la presión son:
• Selectividad del equilibrio Liquido-Vapor. La mayoría
de las mezclas de hidrocarburos incrementan la
volatilidad entre los constituyentes a separar cuando
disminuye la presión. Cuando esto procede con estas
mezclas se recomienda operar a la presión más baja
posible para hacer más fácil la separación y por tanto
se reduce la cantidad de energía requerida.
En el caso de mezclas no ideales la presión también
modifica las características de volatilidad. En
particular modifica la composición del azeótropo y
constituye un factor positivo para la separación.
• Integración de calor. Las consideraciones de
integración de calor pueden resultar muy acertadas
en la selección de la presión desde el punto de vista
económico.
Con una serie de columnas de destilación, el vapor
superior de una columna se puede usar para
alimentar el rehervidor de otra columna, como se
muestra en la Figura 11.
Figura 11. Esquema de integración de calor. Fuente
IFP, 2009.
En la configuración de la Figura 11, la selección de la
presión 1 (P1) para la columna C1 y P2 para la columna
C2 están regidas por las temperaturas T1 y T2 que
permiten el intercambio de calor. De manera similar,
el resultado es una temperatura relativamente alta en
el fondo de la columna C1 lo que supone se dispone
del calor apropiado.
En este esquema no se toma en cuenta la flexibilidad
con respecto al rehervidor de la columna C2.
• Posible uso de sistemas de recompresión de vapor en
tope.
Una forma de evitar las restricciones de temperatura
en la parte superior de la columna impuestas por el
fluido de enfriamiento y al mismo tiempo suministrar
calor para los propósitos del rehervidor. Esto consiste
en comprimir los vapores de tope para elevar su
temperatura de condensación por encima de la
temperatura del fondo de la columna (véase Figura
12).
Figura 12. Esquema típico de sistema de
recompresión de vapor en tope. Fuente: IFP, 2009
• Control de presión.
Una vez, obtenidas las condiciones de operación de la
columna, se procede a aplicar el método corto FUG y sus
variantes: Fenske – Underwood - Gilliland, Winn-Erbar-
Maddox-Kirkbride-Akashah y col). Este método involucra una
estimación del número de platos a reflujo infinito, relación de
reflujo mínimo y número de etapas a reflujo finito para un
fraccionador simple, aun cuando puede aplicarse a columnas
complejas.
• Número de etapas a reflujo total o reflujo infinito.
Ecuación de Fenske.
Fenske (1931) fue el primero de derivar una ecuación para
calcular el número mínimo de platos para columnas de
destilación multicomponente. La deducción exacta para el
número mínimo de etapas requiere sólo la utilización del valor
de la constante de equilibrio (K) y la consideración de igualdad
de fracciones molares entre las etapas (recuérdese el cálculo
gráfico para mezclas binarias por el método de Ponchon-
Savarit y McCabe-Thiele). Para operación en estado
estacionario, la entrada de calor en el calderín y la salida en el
condensador son iguales (suponiendo que no hay pérdidas de
calor) y, según el balance de materia, las corrientes de vapor y
líquido que se cruzan entre dos etapas tienen los mismos
caudales y composiciones. Sin embargo, los caudales de vapor
y líquido variarán de una etapa a otra, a no ser que se cumpla

11. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
la condición de flujo molar constante. Por tanto, el número
mínimo de etapas de equilibrio depende del grado de
separación de los dos componentes clave y de su volatilidad
relativa, pero es independiente de la condición fásica de la
alimentación.
Considérese una columna de destilación multicomponente
que opera a reflujo total como se muestra en la Figura 13.
La relación de equilibrio para el componente clave liviano en el
plato del tope es y1 = K1*x1 (1)
Para un condensador total, y1 = xD, entonces
xD,LK = K1*x1 (2)
Un balance de materia en el volumen de control especificado
en la figura 13, alrededor del tope de la columna y por debajo
del plato del tope: V2 = L1 + D (3)
A condiciones de reflujo total D = 0 y V2 = L1, el balance de
materia en el componente clave liviano en el volumen de
control especificado: V2*y2 = L1*x1 + D*xD,LK (4)
Bajo estas condiciones de platos mínimos y de la ecuación
anterior resulta y2 = x1 (5)
Figura 13. Columna de destilación multicomponente a reflujo
total.
La relación de equilibrio en el plato 2 es y2 = K2*x2, si y2 = x1 la
relación de equilibrio se transforma en: x1 = K2*y2 (6)
Sustituyendo la ecuación (6) en la ecuación (2) se obtiene:
xD,LK = K1*K2*y2 (7)
Continuando este cálculo a lo largo de toda la columna, se
puede obtener la siguiente expresión:
xD,LK = K1*K2*…..*Kn*KB*xB,LK (8)
Por analogía para el componente clave pesado,
xD,HK = K1’*K2’*…..*Kn’*KB’*xB,HK (9)
La división de la ecuación (8) entre la ecuación (9):
89,45
89,<5
ef
egf
∗
eh
eh
i ∗ … ∗
ek
ek
i ∗
e=
e=
i ∗
8=,45
8=,<5
(10)
El valor de la relación de K es la volatilidad relativa, así la
ecuación (10) puede escribirse como:
89,45
89,<5
∗ ∗ … .∗ ∗ ∗
8=,45
8=,<5
(11)
Si la volatilidad promedio aplica para todos los platos y bajo la
condición de platos mínimo, la ecuación (11) puede escribirse:
89,45
89,<5
TRQm
no>k 8=,45
8=,<5
(12)
Resolviendo la ecuación (12) para número de platos mínimos,
Nmin
pqrs
tsu
vw,xy∗vz,{y
vw,{y∗vz,xy,
|
ts}~•€q
(13)
La ecuación 13 es una forma de la ecuación de Fenske. En esta
ecuación Nmin es el número de etapas de equilibrio requeridas
a reflujo total incluyendo el rehervidor parcial.
Una forma alternativa de la ecuación de Fenske se obtiene
multiplicando y dividiendo el producto de las relaciones de
fracciones molares en el destilado y en el residuo por los
caudales de destilado y de residuo, para obtener las funciones
equivalentes de los caudales de LK y HK en el destilado y en el
residuo y puede escribirse como sigue:
pqrs
ts•
‚w∗vw,xyƒ‚z∗vz,{yƒ
‚w∗vw,{yƒ‚z∗vz,xyƒ
„
ts‚}xy {y
⁄ ƒ~•€q
ts•u
†xy
†{y
|u
‡{y
‡xy
|„
ts‚}xy {y
⁄ ƒ~•€q
(14)
La cantidad del componente clave ligero es (D*xD). Esto es igual
a la recuperación fraccionaria del componente clave ligero en
el destilado (FR)D referido a la cantidad del clave liviano
alimentado y el cual se expresa de la siguiente forma:
(D*xD)LK = (FR)D*(F*xF)LK (15)
De la definición de recuperación fraccional se puede escribir:
(B*xB)LK = (1 – (FR)LK)*(F*xF)LK (16)
Sustituyendo las ecuaciones (15) y (16) y la correspondiente
ecuación para el clave pesado en la ecuación (14) se obtiene:
pqrs
tsˆ
‚‰Šxyƒw‚‰Š{yƒz
‹Œ• ‚‰ŠxyƒwŽ‹Œ• ‚‰Š{yƒzŽ
•
ts}~•€q
(17)
Si el número de etapas mínimas es conocido, la recuperación
fraccionaria para un componente no clave ligero o no clave
pesado puede ser calculada mediante la ecuación (17)
eligiendo el componente no clave a determinar como el
componente clave ligero o clave pesado. Si el componente es
escogido como el clave ligero, la fracción de recuperación del
componente no clave ligero (FRNLK)D puede expresarse como:
‰Špxy*w
} pyx/{y*~•€q
pqrs
‚‰Š{yƒz
Œ• ‚‰Š{yƒz
‘ } pxy/{y*~•€q
pqrs
(18)
La ecuación de Fenske como se muestra puede considerarse
rigurosa si (Kister, H., 1992):

12. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
‚ ’e/“eƒ
TRQm
”‚ ’e/“eƒ ‚ ’e/“eƒ … ‚ ’e/“eƒ
n
•
(19)
Sin embargo, la volatilidad relativa promedio puede obtenerse
a partir de una de las siguientes expresiones:
1. Evaluar la volatilidad promedio a la temperatura promedio,
Tprom = (Ttope + Tfondo)/2
2. αprom = (αtope + αfondo)/2
3. αprom = α a la temperatura del plato de alimentación
4. TRQm – SQTH —Q KQ
5. TRQm – SQTH LW mH S —Q KQ
˜
Douglas propuso un criterio para convenir la aproximación de
volatilidad relativa, la desigualdad de Douglas:
™45,š›œA ™45,•›kI›
™45,š›œA‘ ™45,•›kI›
≤ 0,1 ∗ & Ÿ
™45,š›œA‘ ™45,•›kI›
(20)
Cuando se cumple la inecuación de Douglas, la volatilidad
relativa se considera razonablemente constante a lo largo de
la columna y las expresiones más apropiadas para su cálculo
son la 2 o 4.
Cuando hay diferencias considerables entre la volatilidad
relativa entre el tope y fondo de la columna el uso del valor
promedio en la ecuación de Fenske subestimará el número de
etapas a reflujo máximo (Fuente:
http://iq.ua.es/MetAprox/411_clculo_del_nmero_mnimo_de
_etapas.html).
En estas condiciones, un mejor estimado puede hacerse
calculando el número de etapas en la zona de rectificación y en
la zona de agotamiento por separado. La concentración de la
alimentación es tomada como la concentración de fondo para
la zona de rectificación y como la concentración de tope para
la zona de agotamiento, y se estima la volatilidad relativa
promedio para cada sección.
Ecuación de Winn.
Winn (1958) propone una ecuación que considera los efectos
de la variación de la temperatura sobre la volatilidad relativa,
¡m
W ˆ
¢45,9
¢45,=
u
¢<5,=
¢<5,9
|
£45
•
W ¤45 <5
⁄
(21)
Donde ϕLK y βLK/HK son constantes a una presión fija, evaluadas
a partir de los valores K del clave ligero y el clave pesado a las
temperaturas de tope y fondo de la columna, su relación es:
¥’e “e
⁄ 2’e 2“e*¦45
⁄ (22)
Este método no aplica a las mezclas que forman azeótropos o
a condiciones cercanas a las críticas. La ecuación de Winn se
reduce a la ecuación de Fenske cuando ϕLK = 1,0 y
βLK/HK = αLK/HK (Ludwig, E., 1994).
La aplicación de las ecuaciones de Fenske y Winn requiere
haber realizado previamente el balance preliminar de materia,
con el fin de disponer de las composiciones del destilado y del
residuo y poder realizar el cálculo de las volatilidades a la
temperatura de rocío del destilado y de burbuja del residuo. Si,
una vez realizada la comprobación del balance preliminar de
materia se observaran discrepancias muy grandes con los
valores supuestos, se debe repetir el cálculo.
La comprobación del balance preliminar de materia se lleva a
cabo mediante la comparación con la distribución que se
obtiene para los componentes no clave a reflujo total, ya que
ésta proporciona una buena estimación de la separación que
se obtendrá para la columna operando a una razón de reflujo
finita, comprendida entre el reflujo total y el reflujo mínimo.
Resulta evidente que la distribución de los componentes clave
entre el destilado y el residuo ha de ser la misma
independientemente de las condiciones de operación de la
columna ya que se trata de una especificación del problema.
Sin embargo, la distribución de componentes no clave varía
dependiendo de que la columna opere a reflujo total, a reflujo
mínimo o a reflujo intermedio. Una vez que se conoce Nmin,
la ecuación de Fenske y de Winn permite calcular las fracciones
molares xD y xB para todos los componentes no clave. Como ya
se ha dicho, estos valores proporcionan una primera
aproximación a la distribución real de los productos cuando se
utiliza un número de etapas superior al mínimo y, obviamente,
permiten calcular las temperaturas de las etapas de tope y de
fondo, que deberán compararse con los valores estimados
utilizados para el cálculo de las volatilidades en la ecuación de
Fenske y las constantes ϕ y β de Winn.
Estas composiciones calculadas para el destilado y el residuo a
reflujo total deben compararse con las procedentes del
balance preliminar de materia que han servido para iniciar los
cálculos, permitiendo así el cálculo de la volatilidad relativa
media necesaria para aplicar la ecuación de Fenske. En caso
que se observen discrepancias considerables, deberá
reconsiderarse el balance preliminar de materia y repetirse el
cálculo de Nmin y, si es necesario, también de la presión de
operación.
Sea i un componente no clave y r el componente de referencia
en este caso el componente clave pesado. La ecuación 14
adquiere la forma:
‹
†r
‡r
Ž ‹
†•
‡•
Ž ‚}r,•ƒ~•€q
pqrs
(22)
Y sustituyendo fi = di + bi, se obtiene:
‡r
§r
Œ‘‹
†•
‡•
Ž‚}r,•ƒ~•€q
pqrs
(23)
y
†r
§r‹
†•
‡•
Ž‚}r,•ƒ~•€q
pqrs
Œ‘‹
†•
‡•
Ž‚}r,•ƒ~•€q
pqrs
(24)

13. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
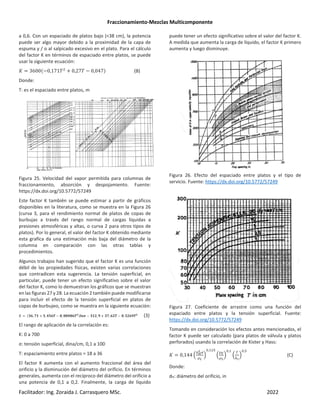
Las ecuaciones 23 y 24 dan la distribución de los componentes
no clave a reflujo total de acuerdo con la ecuación de Fenske.
Un tratamiento análogo de la ecuación de Winn conduce a:
‡r
§r
Œ‘¨
©
r,•
pqrs
‹
‡•
†•
Ž
ªr,•
‹
z
wŽ
Œ•ªr,•
«
(25)
y
†r
§r
Œ‘¨
‹
‡•
†•
Ž
ªr,•
‹
z
w
Ž
Œ•ªr,•
©r,•
pqrs
«
(26)
donde,
¬ ∑ ] (27)
y
_ ∑ # (28)
Para aplicar las ecuaciones 25 y 26 se suponen valores de D y
B y se comprueban después con las ecuaciones 27 y 28.
Para cálculos exactos deberán utilizarse las ecuaciones 23, 24,
25, 26 con el fin de calcular la menor de las dos cantidades bi y
di, mientras que la otra se obtiene mejor mediante un balance
global de materia (Henley, E. J. y Seader, J. D., 1998).
Perfil de concentración a reflujo total.
a. Evolución de la concentración en las dos fases.
La relación entre los caudales de líquido y vapor ponen de
manifiesto la simple correlación que vinculas las
concentraciones entre las fases.
Si se considera la ecuación que relaciona el balance entre
dos platos, de acuerdo al esquema de la Figura 14:
Balance de materia: yip+1 = xip
Relación de equilibrio: yip+1 = Kip+1 xip+1
La combinación de las dos ecuaciones conduce a una
nueva: xip = Kip+1 xip+1
Para la fase de vapor estas ecuaciones son válidas,
Balance de material: yip+2 = xip+1
Relación de equilibrio: yip+1 = Kip+1 xip+1
Figura 14. Esquema de dos platos en una columna de
destilación. Fuente: IFP, 2009.
Combinando las ecuaciones anteriores se tiene:
yip+1 = Kip+1 yip+2
Así, la evolución de la concentración molar de algún
constituyente i puede ser monitoreada por el valor de los
coeficientes de distribución Ki. Dos casos pueden
presentar, si se compara el valor de Ki a 1.
Si Kip+1 es mayor que 1
• El componente i actúa como un componente volátil,
liviano.
• xip > xip+1 y yip+1 < yip+2
• yi incrementa como el vapor se eleva a lo largo de la
columna
• xi disminuye como el líquido fluye hacia el fondo de la
columna.
Si Kip+1 en menor que 1,
• El componente i se comporta como un componente
pesado
• xip < xip+1 y yip´1 > yip+2
• yi disminuye como el vapor se eleva a lo largo de la
columna
• xi aumenta como el líquido fluye hacia el fondo de la
columna.
Ambas situaciones pueden ocurrir para un constituyente
dado porque el coeficiente de distribución varía a lo largo
de la columna con la temperatura. Un ejemplo sencillo para
explicar este fenómeno es la ley de Raoult,
2
Y>
8>
>
-
donde, ®¯
: es la presión de saturación del
componente i y P: es la presión total.
A reflujo total la presión varia solo un poco, entonces las
variaciones de los coeficientes de distribución son debido a
presión de saturación del componente i, medida con la
temperatura: si la temperatura incrementa, la presión de
saturación aumenta también como incrementa el
coeficiente de distribución, moviéndose eventualmente
desde un valor inferior a 1 hasta un valor superior a 1 (Ver
Figura 15)
Figura 15. Curva de presión de vapor del componente i.
Fuente: IFP, 2009.
Si la presión de saturación es igual a la presión total (®¯
®), el valor del coeficiente de distribución es 1,0. Esto
ocurre cuando la temperatura de operación en un plato es
igual a la temperatura de ebullición del componente i, a las
condiciones de presión de operación de la columna.

14. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
Para algunos componentes en la columna, se pueden
encontrar tres situaciones, comparando la temperatura de
operación (T) del plato y la temperatura de ebullición (Tbpi)
del mismo componente i:
• Si T > Tbpi a la presión de operación, entonces la ®¯
>
® y Ki > 1,0. Este componente i se comporta como un
componente liviano y el vapor se va enriqueciendo a
medida que se eleva al tope de la columna, mientras
que el líquido se va empobreciendo en ese componente
i. Esta situación ocurre preferiblemente cercana al tope
de la columna.
• Si T < Tbpi a la presión de operación, entonces la ®¯
C
® y Ki < 1,0. Este componente i se comporta como un
componente pesado y el vapor se empobrece en el a
medida que sube hacia el tope de la columna, mientras
que la fase liquida se enriquece en el componente i.
Generalmente esto ocurre preferiblemente cercano al
fondo de la columna.
• Si la T = Tbpi a la presión de la columna, entonces la ®¯
® y Ki = 1,0. Estas condiciones sobre un plato en
específico indican que la concentración del
componente i será la misma en ambas fases, liquido-
vapor. En las cercanías de este plato, otras situaciones
pueden tomar lugar, primero un máximo de
concentración sobre el plato si la T = Tbpi.
Perfil de concentración.
• Relación mínima de reflujo. Ecuación de Underwood
En la Figura 16 se pueden distinguir tres tipos de
compuestos
Figura 16. Diagrama para identificar los compuestos en la
columna. Fuente: IFP, 2009.
Así la temperatura de ebullición de los componentes en la
alimentación puede ser:
• Más altas que la temperatura de tope (Componentes
ligeros)
• Más bajas que la temperatura de fondo
(Componentes pesados)
• Entre las temperaturas de tope y fondo de la columna
(componentes intermedios).
Esto corresponde a tres situaciones diferentes de los
perfiles de concentración:
• Para los constituyentes livianos (grupo a, b y c), la
temperatura de operación está en cualquier punto de
la columna más alta que la temperatura de ebullición.
Esta concentración disminuye de tope a fondo.
• Para los constituyentes pesados (grupo g), la
temperatura de operación en cualquier punto de la
columna es más baja que la temperatura de
ebullición. Su concentración incremente de tope a
fondo.
• Para los componentes intermedios (grupo d, e y f),
ellos se comportan como componentes pesados en el
tope y como componentes livianos en el fondo. Así, su
perfil de concentración muestra un máximo sobre la
etapa donde la temperatura es cercana a su
temperatura de ebullición, como se observa en la
Figura 17.
Figura 17. Perfil de concentración a reflujo total. Fuente: IFP,
2009.
Para sistemas binarios el punto de estricción suele presentarse
en el plato de alimentación. Cuando esto sucede, se puede
obtener la solución analítica para los flujos límites que también
es válida para sistemas multicomponente, siempre y cuando el
punto de estricción este en la etapa de alimentación (Wankat,
P., 2008). A diferencia de los sistemas binarios, en los sistemas
con varios componentes, si hay componentes no distributivos,
habrá puntos de estricción separados en las secciones de
agotamiento y enriquecimiento.
Shiras, Hanson y Gibon (Tomado de Seader y col. 1998)
clasifican el punto de estricción (punto pinch) para mezclas
multicomponente en:
Clase 1: todos los componentes de la alimentación se
distribuyen en ambos productos destilado y fondo. La zona de
contacto aparece en los platos adyacentes al plato de
alimentación, salvo en casos similares al que se da en mezclas
binarias no ideales en las que la recta operativa que determina
el reflujo mínimo sea una tangente a la curva de equilibrio. En
este caso, la zona de composición constante aparece en el
sector en el que se encuentre dicho punto de tangencia.
Ocurrirán separaciones de clase 1 en el caso de mezclas con un
estrecho margen de temperaturas de ebullición, o cuando el
grado de separación entre los componentes clave no sea muy
grande.

15. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
Clase 2: Uno o más componentes aparecen solo en uno de los
productos. Si hay componentes NLK no distribuidos, aparece
una zona de contacto en el sector de agotamiento, separada
del piso de alimentación, y los pisos comprendidos entre el de
alimentación y la zona de contacto sirven para eliminar los
componentes ligeros que no aparecen en el residuo. Si hay
componentes NHK no distribuidos, aparece una zona de
contacto en el sector de enriquecimiento, y las etapas entre el
piso de alimentación y la zona de contacto sirven para eliminar
los componentes pesados que no aparecen en el destilado.
En la Figura 18 se muestran los puntos de estricción de acuerdo
a la clasificación dada por Shiras y col.
En mezclas multicomponente los componentes distribuidos se
encuentran en ambas corrientes, tope y fondo; los
componentes no distribuidos se encuentran en una sola
corriente; si la volatilidad del componente clave pesado es
menor a 0,9 (αHK < 0,9), entonces los componentes pesados no
se distribuyen; si la volatilidad del componente clave liviano es
mayor a 1,1 (αHK > 1,1), entonces los componentes clave liviano
no se distribuyen.
Figura 18. Puntos de estricción en sistemas de varios
componentes.
Colburn (1941) y Underwood (1949) deducen las ecuaciones
para estimar la relación de reflujo mínimo para destilaciones
multicomponente. Sin embargo, la ecuación de Underwood es
más ampliamente usada es la que se presenta en esta sección.
El método de Underwood da una rápida estimación de los
requisitos de reflujo mínimo, cuando se especifican las
composiciones del destilado y los productos de cola. Asume
flujo molar constante en las zonas intermedias y la volatilidad
relativa constante a la temperatura media de la columna.
Aunque las composiciones deben ser estrictamente las de
reflujo mínimo, los valores determinados a reflujo total, por la
ecuación de Fenske, se pueden usar. Un mejor estimado puede
obtenerse reemplazando el número de etapas a reflujo total
de la ecuación 21 por una estimación del número real; un valor
igual a Nmin/6 es frecuentemente usado.
Este método consiste en determinar el valor de una constante
θ que se encuentra numéricamente entre la volatilidad relativa
de los componentes clave y satisface la ecuación:
`
∗ Ea>
− ±
1 − ,
F
Deben determinarse n-1 valores de θ, donde n es el número
de componentes que se distribuyen. Luego, este factor θ se
sustituye en una segunda ecuación, que se muestra a
continuación, y relaciona el reflujo mínimo con la volatilidad
relativa y la composición del destilado:
u
1
_
|
m
+ 1 `
∗ E3>
− ±
F
Cuando los componentes clave son adyacentes es decir, no hay
componentes no clave distribuidos, el método se desarrolla de
la siguiente manera:
`
∗ Ea>
− ±
∗ Eaf
− ±
+
∗ Eah
− ±
+ ⋯ +
∗ Eak
− ±
1 − ,
F
Donde:
αi = volatilidad del componente i referida al componente clave
pesado.
xFi: composición del componente i, en la alimentación.
q: número de moles de líquido saturado formado en el plato
de alimentación por la introducción de un mol de
alimentación.
Los valores validos de θ están entre las volatilidades relativas
de los componentes clave, αHK/HK < θ < αLK/HK y se determina por
ensayo y error. Luego de obtenido el valor de θ, se sustituye
en la segunda ecuación de Underwood, como se muestra a
continuación:
u
1
_
|
m
+ 1
∗ E3f
− ±
+
∗ E3h
− ±
+ ⋯ +
∗ E3k
− ±
Otros métodos también están disponibles para el cálculo de
reflujo mínimo. Van Winkle recomienda el método de
Underwood’s, el método de Brown-Martin y el método de
Colburn (Kister, H., 1998).
Método de Brown-Martin: este método se basa en la
observación del punto de estricción en la alimentación, la
relación de los componentes clave es esencialmente igual a su
relación en la alimentación de líquido. Este método es menos
complicado y es adecuado para estimaciones conservadoras.
Es adecuado principalmente para hidrocarburos en situaciones
donde no se requiere gran precisión.
Método de Colburn: este método calcula la relación de reflujo
mínima de los componentes clave como si formaran una
mezcla binaria, corrige este valor para los no clave ligero y no
clave pesado. El método de Colburn asume flujo molar

16. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
constante y volatilidad relativa constante en cada zona de
composición constante de la columna. Este método es más
elaborado, pero ha sido recomendado como el más adecuado
método corto para reflujo mínimo.
Si hay presencia de componentes no clave distribuidos estos
aparecen en ambas corrientes de producto destilado y fondo.
Generalmente, los componentes no clave no se distribuyen, es
decir, a reflujo mínimo los componentes no clave pesado están
totalmente contenidos en la corriente de fondo y los
componentes no clave ligero están contenidos en la corriente
de destilado. Un componente no clave se distribuirá si:
• Si estos tienen una volatilidad muy cercana a uno de los
componentes clave, o
• Si la separación especificada de los clave no es nítida, o
• Si los componentes no clave tienen volatilidad intermedia
entre los clave.
Shiras y col. (1950), desarrollan una ecuación para verificar la
distribución de los componentes no clave a reflujo mínimo:
_³
_ ∗ E3>
d ∗ Ea>
− 1
’e − 1
∗
_ ∗ E3,’e
d ∗ Ea,’e
+
’e −
’e − 1
∗
_ ∗ E3,“e
d ∗ Ea,“e
Los criterios a aplicar para esta ecuación son los siguientes:
DR > 1 El componente no se distribuye y sale
exclusivamente por la corriente de destilado
0 < DR < 1 El componente se distribuye, y el valor de DR es
la recuperación del componente en el destilado
DR < 0 El componente no se distribuye y sale
exclusivamente por la corriente de fondo.
En sistemas que contienen componentes no clave distribuidos,
se plantea la primera ecuación de Underwood tantas veces
como valores de θ se tengan para conocer los valores de
(L/D)min y las composiciones (xDi) o la cantidad (di) de los
componentes no clave distribuidos en la corriente de
destilado. Es decir, se obtienen n-1 valores de θ, donde n es el
número de componentes que se distribuyen; las
composiciones o las cantidades de los componentes no clave
distribuidos no son conocidas y el destilado total es la
sumatoria de las cantidades individuales de los componentes
que sale por la corriente de tope, D = d1 + d2 + … + dn.
La segunda ecuación de Underwood se transforma en:
`
∗ E3>
− ±
u
1
_
|
m
+ 1
1m + _
_
F
`
∗ #
− ±
1m + _
F
Desarrollando la ecuación se tiene:
∗ #
− ±
+
∗ #
− ±
+ ⋯ +
∗ #
− ±
1m + _
∗ #
− ±
+
∗ #
− ±
+ ⋯ +
∗ #
− ±
1m + _
.
∗ #
− ±
+
∗ #
− ±
+ ⋯ +
∗ #
− ±
1m + _
D = d1 + d2 +… + dn y Rmin = (L/D)min
Si resulta que los valores de di son negativos o mayores a lo
alimentado a la columna (fi) el componente “i” no se distribuirá
y los componentes clave se habrán escogido en forma
incorrecta. Además, si el valor de Rmin obtenido no es lógico
(muy grande), los componentes clave deberán ser elegidos
nuevamente.
Debido a que el procedimiento para determinar el valor de θ
es largo y tedioso Maddox y Hines (1985) muestran la solución
grafica desarrollada por Van Winkle y Todd (1971) para el caso
de una separación donde solo se distribuyen los componentes
clave y la alimentación está en su punto de burbuja, en la
Figura 19 se presenta el grafico utilizado para esta solución
gráfica. El valor de θ (φ símbolo utilizado por Van Winkle y
Todd), es determinado usando el valor de la volatilidad, αLK,F, y
la relación de las composiciones de los componentes clave en
la alimentación (xLK/xHK)F. Este valor debe verificarse con la
primera ecuación de Underwood, ya que la Figura 19 solo da
un estimado del valor de θ.
Figura 19 Valor de θ (φj) y relación de los componentes clave
en la alimentación. Fuente: Hines, A. L. y Maddox, R. N., 1985.
El valor de θ leído en la Figura 19 debe ser exacto para una
mezcla binaria que solo contiene los componentes clave, ligero
y pesado. Para mezclas que contienen más de dos
componentes, el valor leído en la figura es solo un estimado.
Cuanto mayor sea el grado en que los componentes clave
dominen la composición de la alimentación, más cercano será
el valor de α. “Nunca, sin embargo, para una mezcla

17. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
multicomponente debe leerse un valor de θ de la figura 19 y
usarse directamente para el cálculo del reflujo mínimo”, este
valor debe chequearse, mediante la primera ecuación de
Underwood (Hines, A. L., y Maddox, R. N., 1985).
En el caso de columnas complejas se han utilizado distintos
enfoques para el cálculo de reflujo mínimo. Barnés y col.
(1972) realizaron una extensión de la ecuación de Underwood
a columnas de alimentación múltiple. El reflujo mínimo en
cada sección entre dos alimentaciones adyacentes se
considera por separado. El clave liviano en el vapor de salida
de cada sección es usado en la primera ecuación de
Underwood, y puede calcularse restando la cantidad del clave
ligero que entra en la sección por encima de la alimentación y
el clave ligero en el producto de tope. Un factor que complica
la situación es la presencia de componentes distribuidos
(Kister, H., 1992).
Reflujo de operación y etapas teóricas.
La relación de reflujo de operación se establece generalmente
por consideraciones económicas como un múltiplo del reflujo
mínimo. Se determina entonces el correspondiente número de
etapas teóricas utilizando un adecuado método analítico,
grafico o bien mediante una ecuación empírica. Sin embargo,
no existe una razón por la cual el número de etapas teóricas
no pueda especificarse como un múltiplo del número mínimo
de etapas y calcular el reflujo de operación por la misma
correlación empírica, como se muestra en la Figura 20.
En la Figura 20, se observa que el valor óptimo de la relación
R/Rmin es aproximadamente 1,05. En la práctica para los
superfraccionadores que requieren un gran número de etapas
la relación R/Rmin es 1,10; para los separadores que requieren
un menor número de etapas R/Rmin es 1,50 y para los casos
intermedios R/Rmin es 1,30.
Figura 20. Efecto de la relación de reflujo sobre el costo.
Fuente: Henley, E. J., y Seader, J. D., 1998
Diferentes autores han presentado correlaciones que
relacionan empíricamente la cantidad de etapas (N = S) a
relación de reflujo (L/D) finita, con la cantidad mínima de
etapas Nmin y con la relación mínima de reflujo (L/D)min. Uno de
los más conocidos es el propuesto por Gilliland (1940) y el
presentado por Brown y Martin (1939). Aunque estas
correlaciones son útiles para realizar los análisis económicos
preliminares, Gray (1969) y Erbar-Maddox (1961)
desarrollaron una correlación un poco más exacta que
requiere el uso de más de una curva. Las líneas curvas de la
Figura 16 representan la relación mínima de reflujo (L/V)min
para una separación especificada. Al leer verticalmente desde
el eje X (Nmin/N) hasta la relación mínima de reflujo, se puede
determinar la relación de reflujo de operación.
Método de Gilliland.
La grafica de Gilliland correlaciona el reflujo y las etapas
mediante la ecuación que se muestra a continuación (ver
Figura 20a-b):
´
0 − 0m
0 + 1
^ µ
¡ − ¡m
¡ + 1
Si R = L/D = Rmin, X = 0, entonces Y se aproxima a la unidad. Si
N = S = Nmin, Y = 0, entonces X se aproxima a la unidad.
La correlación de Gilliland se obtiene a partir de 61 datos
experimentales y cubren los siguientes intervalos de
condiciones:
• Número de componentes: 2 a 11
• q: 0,28 a 1,42
• Presión: vacío hasta 600 psig
• α: 1,1 a 4,05
• Rmin: 0,53 a 9,09
• Nmin: 3,4 hasta 60,3
Figura 20a. Correlación de Gilliland (S = N) en coordenadas log-
log. Fuente: Hines, A. L. y Maddox, R. N., 1985.
De acuerdo con la Figura 20b un pequeño incremento inicial
de R por encima de Rmín provoca una gran disminución de N,
pero incrementos posteriores ya no tienen tanta influencia

18. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
sobre el número de platos. El cambio brusco de pendiente
corresponde a la relación de reflujo óptima.
Figura 20b. Correlación de Gilliland en coordenadas lineales.
Fuente: Hines, A. L. y Maddox, R. N., 1985.
Se realizaron varios ajustes de la curva de Gilliland mediante
métodos numéricos, entre ellos la ecuación de Eldujee (1975),
ecuación de Chang (1981) y la de Molokanov y col. (1972). La
ecuación de Eduljee tiene la ventaja de ser muy simple. King,
C. J. (1979) sugiere usar la ecuación de Eduljee donde no se
requiere alta precisión y Molokanov cuando se desea una
mejor precisión.
La ecuación de Eduljee está dada por:
n no>k
n‘
0,75 •1 − ‹
³ ³o>k
³‘
Ž
,O¶¶
„
Válida para ‹
³ ³o>k
³‘
Ž > 0,01
La ecuación de Chang está dada por:
n no>k
n‘
1 − $E+ ·1,490 + 0,315 ‹
³ ³o>k
³‘
Ž −
, O
‹
º•ºo>k
º»f
Ž
¼,f½
La ecuación de Molokanov está dada por:
µ
¡ − ¡m
¡ + 1
1 − $E+ •u
1 + 54,4´
11 + 117,2´
| u
´ − 1
´ ,O
|„
´
0 − 0m
0 + 1
Esta ecuación cumple con los puntos extremos (Y = 0, X = 1) e
(Y = 1, X = 0). Para el valor de R/Rmin próximo al óptimo de 1,3,
la Figura 16b predice una relación óptima para N/Nmin de
aproximadamente 2. El valor de N incluye una etapa para un
ebullidor parcial y otra para un condensador parcial.
Método de Erbar-Maddox
Este método grafica (ver Figura 21) a R/(R+1) contra Nmin/N,
con Rmin/(Rmin + 1) como parámetro. Cuando R = Rmin el eje x da
cero. Por lo tanto, el eje “y” del diagrama representa
condiciones de reflujo mínimo. Cuando N = Nmin, ambos ejes
coordenados “x” y “y” son la unidad.
La grafica de Erbar – Maddox está basada en una alimentación
en su punto de burbuja. Para otros tipos de alimentación, la
siguiente correlación es usada:
c
¾ c¿ +
1 − _ d
⁄ *‚;a,¾ − ;a,¿ƒ
ÀP 1Q
⁄
Donde:
Vu: es el flujo de vapor en la sección de rectificación, si la
alimentación está en una condición diferente a su punto de
burbuja, lbmol/h
Vk: es el flujo de vapor en la sección de rectificación, si la
alimentación está en su punto de burbuja, lbmol/h
D: flujo de destilado, lbmol/h
F: flujo de alimentación, lbmol/h
HF,u: entalpia de la alimentación a condiciones diferente a su
punto de burbuja, Btu/h
HF,k: entalpia de la alimentación a condiciones de burbuja,
Btu/h.
Qc: calor en el condensador, Btu/h
Lo: Flujo de líquido condensado, lbmol/h
En la correlación de Erbar-Maddox, las etapas mínimas son
calculadas por el método de Winn y el reflujo mínimo por el
método de Underwood, pero también puede usarse la
ecuación de Fenske para el número mínimo de etapas (Kister,
H., 1992).
Muchos diseñadores recomiendan ambas correlaciones,
Gilliland y Erbar-Maddox. La correlación de Erbar-Maddox es
considerada más adecuada, especialmente a bajas relaciones
de reflujo; sin embargo, la precisión de la ecuación de Gilliland
para una exploración preliminar de las variables de diseño es
usualmente satisfactoria.
Es importante utilizar consistentemente las correlaciones de
reflujo mínimo/etapas mínimas/reflujo-etapas. Ambos
métodos, Gilliland y Erbar-Maddox, son consistentes con la
ecuación de Fenske y el método de Underwood.
Robinson y Gilliland (tomado de Henley, E. J., y Seader, J. D.,
1998) indican que una correlación más exacta habría de utilizar
un parámetro en el que intervenga la condición
termodinámica de la alimentación, q. Estudios realizados,
que cubren la condición termodinámica de la alimentación
desde liquido frio a vapor sobrecalentado (q desde 1,3 hasta -
0,7), muestran una tendencia hacia la disminución del número
de etapas necesarias al aumentar la vaporización de la
alimentación. En general, la correlación de Gilliland presenta
problemas cuando el agotamiento es más importante que la
rectificación, debido a que no se tiene en cuenta el caudal de

19. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
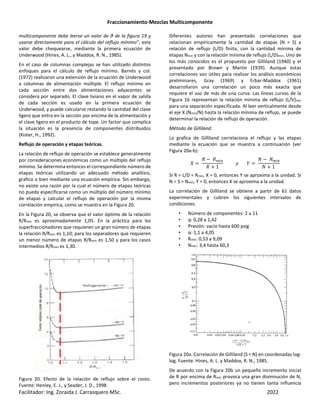
vapor generado en la caldera ("vaporización"). Por otro lado,
esta correlación tampoco tiene en cuenta la condición térmica
del alimento, y tiende a ser conservadora para alimentos con
fracciones líquidas bajas. El efecto de la condición térmica del
alimento puede llegar a ser importante cuando la volatilidad
relativa de componente clave liviano respecto de componente
clave pesado es alta o cuando el alimento es pobre en
componentes volátiles.
Figura 21. Correlación de Erbar-Maddox. Fuente: Hines, A. L. y
Maddox, R. N., 1985.
Localización de la etapa de alimentación.
Todos los trabajos realizados están fundamentados en la
asunción de que la alimentación será introducida en la
ubicación óptima de la columna. El óptimo, el cual está basado
solo en las consideraciones del fraccionamiento, es difícil de
establecer claramente pero se puede decir de dos maneras:
para un reflujo dado el plato de alimentación es el que
requerirá el menor número de contactos teóricos para lograr
la separación deseada, o para un numero de etapas dadas el
plato de alimentación será el que requiere el menor reflujo
para lograr la separación deseada.
Las correlaciones más usadas son la ecuación de Fenske y la de
Kirkbride, ambas son aproximaciones. La relación de Fenske
(1932) estima la localización del plato de alimentación.
Básicamente, se supone que la proporción de los platos en la
sección de rectificación es constante e independiente de la
tasa de reflujo. Las ecuaciones para la zona de rectificación y la
zona de agotamiento en la columna son:
nº u
#
|
’e
u
#
|
“e
#’e
’e
“e
#“e
n- u
]
|
’e
u
]
|
“e
’e
]’e
]“e
“e
Donde NR representa el número de etapas por encima del plato
de alimentación y NS es el número de etapas en la zona de
agotamiento. Se considera que la volatilidad relativa es
constante a lo largo de la columna y se calcula a la temperatura
promedio y presión de la columna.
Un procedimiento alternativo, que probablemente sea una
estimación más exacta de la ubicación del plato de
alimentación, es el método de Kirkbride (1944) (Wankat, P.,
2008). La relación de la cantidad de platos en la zona de
rectificación, NR, entre la cantidad de platos en la zona de
agotamiento, NS, puede estimarse con la siguiente ecuación:
Á u
¡³
¡¯
| 0,260 ∗ Á ·
¬
_
Â
E“e,a
E’e,a
à Â
E’e,
E“e,3
à ½
Akashah y col (1979) presento una modificación de la ecuación
de Kirkbride, como sigue:
¡³ ¡³Ä(! ( !# + " ! $(. #$ 2%"D]"%#$Å − 0,5 ∗ Á¡
Capacidad, diámetro y altura de la columna
En aplicaciones industriales, el diámetro de las columnas de
fraccionamiento varía grandemente y están en el rango de 65
cm para columnas muy pequeñas y 6 m para columnas
grandes, incluso hasta 15 m o 50 ft en algunas aplicaciones. En
general, el diámetro de la columna es relativamente insensible
a los cambios de temperatura o presión de operación. No
obstante, el dimensionamiento adecuado del diámetro de la
columna es esencial para el rendimiento y operación eficiente
de la columna de fraccionamiento. Si el diámetro de la
columna no se dimensiona adecuadamente, pueden ocurrir
problemas operativos y no se logrará la separación deseada. El
dimensionamiento adecuado del diámetro de la columna
también es crucial para otras consideraciones económicas, ya
que el costo del equipo de fraccionamiento está muy
influenciado por el diámetro de la columna. Es importante
señalar que se prefiere usar, como dispositivo de contacto, los
empaque para torres pequeñas mientras, que los platos se
usan en torres más grandes, con diámetros mayores a 3 ft.
Entre los factores de diseño de la columna de platos que
dependen del diámetro de la misma, se incluyen el tipo de
plato y la disposición del flujo del líquido en el plato. Los
dispositivos de contacto más usados son los platos de copas de
burbujeo, platos perforados y platos de válvula. En los tres
dispositivos el vapor asciende verticalmente, contacta en cada
plato con el líquido que circula en flujo cruzado o flujo en
contracorriente, como se muestra en la Figura 22. En platos
con flujo cruzado, el vapor fluye solamente a través de los
orificios o perforaciones de los platos, mientras que el líquido
desciende de un plato a otro solamente por el tubo de
descenso (downcomer). Una cantidad de líquido es retenido
sobre el plato por el vertedero (weir), Figura 23. Y en los platos
con flujo en contracorriente (no tienen bajantes) el líquido cae
por la columna a través de una gran abertura en los platos, a
veces son llamados platos de ducha; este tipo de plato se usan
para fines especiales, particularmente cuando se requiere un
baja caída de presión (Sinnot, R. K., 2005).

20. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
Los platos de flujo cruzados son también clasificados de
acuerdo al número de pasos sobre el plato. En la Figura 22a se
muestra el plato de un solo paso; para bajos flujos de líquido
se usan los platos de flujo en reverso, Figura 22b. Este tipo de
plato es dividido por una partición central y la entrada y salida
del bajante está en el mismo lado del plato. Platos de múltiples
pasos, donde la corriente de líquido se subdivide mediante el
uso de varios bajantes y son utilizados para altas tasas de
líquido y diámetros de columna muy grandes. En la Figura 24c,
se muestra un plato de doble paso.
Figura 22. Formas de flujo en columnas de platos de contacto
vapor-liquido. (a) Flujo cruzado y (b) Flujo en contracorriente.
Fuente: Seader, J. D. Henley, E., 1998.
Figura 23. Esquema de plato de flujo cruzado. Fuente:
Figura 24. Patrones de flujo de líquido, (a) paso simple; (b) flujo
en reverso y (c) dos pasos. Fuente: Sinnot, R. K., 2005.
La elección del flujo de líquido, flujo reverso o directo, y el
número de pasos, pasos simples o múltiples, dependen del
diámetro de la columna. El uso de platos de doble paso, por
ejemplo, tiene numerosas ventajas sobre otros tipos de platos,
particularmente en los servicios de ensuciamiento, pero su uso
el torres de diámetros grandes puede conducir al mismo
tiempo a una mala distribución. La práctica común de diseño
es minimizar el número de pasos, por tanto, en platos de
diámetros menores a 1,5 m rara vez usan más de un paso y
aquellos con diámetros entre 1,5 a 3 m rara vez usan más de
dos pasos. Los platos de cuatro pasos se usan en torres de más
de 5 m de diámetros. En general, el aumento del diámetro de
la columna proporciona un aumento del flujo de líquido, con
una relación de diámetro al cuadrado. Como el área disponible
para el flujo de líquido también aumenta en relación al
diámetro, la carga liquida por unidad de longitud del vertedero
de salida aumentara en proporción al diámetro.
Asimismo, en diámetros de columna más grandes, la diferencia
de nivel de líquido a través de la bandeja aumenta
conduciendo a una mezcla ineficiente de líquido y vapor y los
platos pueden tener que equiparse con múltiples bajantes
para reducir las cargas de líquido a través de cada sección del
área activa. . Esto reduce la carga del vertedero y la carga de
líquido en el área activa del plato, lo que da como resultado
una mayor capacidad de vapor, una menor caída de presión y
un mejor rango operativo. Además, la eficiencia del plato, que
generalmente varía entre 40 y 120%, puede verse afectada por
el diámetro de la columna. Debido a un efecto de flujo cruzado,
se pueden lograr valores de eficiencia más altos en la torre de
gran diámetro. Finalmente, los platos de un diámetro mayor
de 900 mm se fabrican normalmente en secciones
dimensionadas para ajustarse a través de los pasillos de las
columnas y se montan dentro de la columna.
El cálculo del diámetro de la columna dependerá de muchos
factores de diseño de la columna, tal como el espaciado entre
platos, el tipo de plato utilizado en la columna, la tensión
superficial y otras propiedades físicas del vapor y líquido a las
condiciones de operación en el plato. Sin embargo, la
interrelación de estos diferentes factores no está muy clara, y
el diámetro está, por lo tanto, determinado por correlaciones
empíricas.
Un espaciado entre platos alto aumenta la capacidad, lo que
genera un diámetro de torre menor, pero al mismo tiempo
aumenta la altura de la torre. En este caso, se debe considerar
una compensación económica entre la altura y el diámetro de
la torre. Por consideraciones de accesibilidad y
mantenimiento, el espaciado entre platos debe ser de 450 a
600 mm. En torres con un diámetro mayor de 1,5 m, el
espaciado entre platos es típicamente de 600 mm para
permitir un fácil acceso para el mantenimiento, pero en torres
muy grandes (> 6 m de diámetro), a menudo se utilizan
espaciados de 750 mm. Para un diámetro de columna por
debajo de 1,5 m, se adecua una separación de platos de 450

21. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
mm ya que se puede alcanzar la pared de la columna desde la
entrada.
El diámetro de la columna es una función de la eficiencia del
plato y de sus características de capacidad, representadas por
los efectos de velocidad, incluido el arrastre y la presión de
operación. Las operaciones de baja presión requieren
generalmente una columna de gran diámetro. Igualmente, la
relación de reflujo es otro factor que afecta el cálculo del
diámetro de la torre. Al aumentar la relación de reflujo significa
que se va a hervir más vapor y que el diámetro requerido de la
columna será mayor.
El factor principal que determina el diámetro de la columna es
la velocidad de flujo de vapor. La velocidad mínima de flujo de
vapor requerida se determina por el lloriqueo (goteo), y la
condición de inundación fija el límite superior de la velocidad
del vapor. Se necesitará una alta velocidad de vapor para lograr
altas eficiencias en el plato, pero la velocidad del vapor debe
estar al mismo tiempo por debajo de la que causaría un
arrastre excesivo de líquido o una caída de presión alta. En
general, la velocidad del vapor normalmente estará entre el 70
y el 90 por ciento de lo que causaría inundaciones. Para
propósitos de diseño, se debe usar un valor de 80 a 85 por
ciento de la velocidad de inundación.
El cálculo del diámetro de la columna a menudo se basa en una
metodología de ensayo y error. El diámetro preliminar
calculado puede ser ajustado comprobando las correlaciones
de rendimiento de la columna. En cualquier caso, el diámetro
calculado también debe redondearse apropiadamente para la
estandarización de la fabricación. Se pueden usar varias reglas
generales antes de llevar a cabo los cálculos reales, pero estas
reglas a menudo tienen excepciones y es posible que no se
apliquen en todos los casos. Entre las reglas relacionadas con
el diámetro de la columna se incluyen las siguientes:
1. La relación de longitud a diámetro debe ser inferior a 30,
preferiblemente inferior a 20, y la altura de la torre debe
limitarse a 60 metros debido a las cargas de viento y los
efectos de la cimentación. Si la torre tiene más de 60 m, se
debe considerar un diseño con un espaciado de bandeja
más pequeño, o utilizar dos torres que funcionen como una
sola.
2. La relación del diámetro de la torre al tamaño del empaque
aleatorio es mayor de 10.
3. El diámetro de la torre debe mantenerse a 1,2 metros en la
parte superior para la desconexión del vapor.
4. El diámetro de la torre debe mantenerse a 2 metros en la
parte inferior, para el nivel de líquido y el retorno de vapor
del rehervidor.
En la práctica normal, sin embargo, solo se calcula un diámetro
para toda la columna. Diámetros diferentes en la columna solo
se usaría cuando haya un cambio de caudal considerable. Se
pueden permitir cambios en la velocidad del líquido mediante
el ajuste de las áreas del bajante. Si la diferencia entre los
diámetros obtenidos en las secciones superior e inferior (o
intermedia) de la columna exceden el 20% y las secciones
tienen al menos 600 cm (20 pies) de longitud, es probable que
resulte más económico usar los diferentes diámetros
obtenidos en las secciones superior e inferior. De lo contrario,
el diámetro debe ser uniforme. El diámetro preliminar de la
columna sería entonces el mayor de los dos diámetros
calculados.
Para el diseño de una columna de platos se deben calcular el
diámetro de la columna que evite la inundación, diseñar la
distribución del plato y diseñar los bajantes. En la literatura se
encuentran varios procedimientos para el cálculo del diámetro
de columna (Fair, 1984; Kister, 1992; Ludwig, 1997; McCabe,
2005). Además, es común que cada fabricante de equipo tenga
su propio procedimiento. Acá, se seguirá uno de los
procedimientos más usados, como lo son el método de
Sourders-Brown, Fair y un método sencillo y aproximado dado
por Heaven.
La ecuación más frecuentemente usada para el cálculo del
diámetro está basada en la bien conocida correlación empírica
de Souders y Brown (Ecuación A). La ecuación A, o la gráfica
de la figura 25 pueden ser usadas para estimar la máxima
velocidad superficial del vapor, y por tanto el área y el
diámetro de la columna.
ÆÇ
e
ȶ
‹
É4 ÉÊ
ÉÊ
Ž
,O
(A)
Donde:
UV: es la máxima velocidad superficial del vapor, m/s o ft/s
ρL : densidad del líquido, kg/m3
o lb/ft3
ρV : densidad del vapor, kg/m3
o lb/ft3
K: es un factor relacionado con el arrastre que depende de
varias variables que difieren de una correlación a otra.
Seader y col (1998) indican que Souders y Brown
correlacionaron los datos de inundación por arrastre para 10
columnas comerciales de platos suponiendo que el transporte
de las gotas en suspensión controla la magnitud del arrastre.
Para bajas velocidades de vapor las gotas sedimentan,
mientras que para altas velocidades son arrastradas. Para la
velocidad de inundación, UV o Uf, la gotita está suspendida de
tal forma que la suma de la velocidad vectorial de las fuerzas
gravitacionales, flotación y rozamiento que actúan sobre ella
es cero. Así, ∑F = 0 = Fg – Fb – Fd y en función del diámetro de
la gota, dp:
Ë’ ‹
ÌKœ̃
¶
Ž Á − ËÇ ‹
ÌKœ̃
¶
Ž Á − Í3 ‹
ÌKœ
h
Î
Ž
Ï•
h
ËÇ 0
Las otras variables principales que afectan el factor K incluyen
espaciado de plato, tipo de plato, propiedades físicas, cargas
de líquido, diámetro del orificio y área fraccional del orificio.
De todas estas variables, el espaciado entre platos es el más
importante. En general, el factor K aumenta con el espaciado
entre platos, a una proporcionalidad con una potencia de 0,5

22. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
a 0,6. Con un espaciado de platos bajo (<38 cm), la potencia
puede ser algo mayor debido a la proximidad de la capa de
espuma y / o al salpicado excesivo en el plato. Para el cálculo
del factor K en términos de espaciado entre platos, se puede
usar la siguiente ecuación:
2 3600 −0,171N + 0,27N − 0,047* (B)
Donde:
T: es el espaciado entre platos, m
Figura 25. Velocidad del vapor permitida para columnas de
fraccionamiento, absorción y despojamiento. Fuente:
https://dx.doi.org/10.5772/57249
Este factor K también se puede estimar a partir de gráficos
disponibles en la literatura, como se muestra en la Figura 26
(curva 3, para el rendimiento normal de platos de copas de
burbujas a través del rango normal de cargas líquidas a
presiones atmosféricas y altas, o curva 2 para otros tipos de
platos). Por lo general, el valor del factor K obtenido mediante
esta grafica da una estimación más baja del diámetro de la
columna en comparación con las otras tablas y
procedimientos.
Algunos trabajos han sugerido que el factor K es una función
débil de las propiedades físicas, existen varias correlaciones
que contradicen esta sugerencia. La tensión superficial, en
particular, puede tener un efecto significativo sobre el valor
del factor K, como lo demuestran los gráficos que se muestran
en las figuras 27 y 28. La ecuación 2 también puede modificarse
para incluir el efecto de la tensión superficial en platos de
copas de burbujeo, como se muestra en la siguiente ecuación:
2 ÐÑ, ÒŒ + Ó, ÔÓÑÕ − Ö, Ö×Ô×ÑÕØ*tsÙ − ÐŒØ, Ú + ÐÒ, ÑØÕ − Ö, ÓØÑÚÕØ
(3)
El rango de aplicación de la correlación es:
K: 0 a 700
σ: tensión superficial, dina/cm, 0,1 a 100
T: espaciamiento entre platos = 18 a 36
El factor K aumenta con el aumento fraccional del área del
orificio y la disminución del diámetro del orificio. En términos
generales, aumenta con el recíproco del diámetro del orificio a
una potencia de 0,1 a 0,2. Finalmente, la carga de líquido
puede tener un efecto significativo sobre el valor del factor K.
A medida que aumenta la carga de líquido, el factor K primero
aumenta y luego disminuye.
Figura 26. Efecto del espaciado entre platos y el tipo de
servicio. Fuente: https://dx.doi.org/10.5772/57249
Figura 27. Coeficiente de arrastre como una función del
espaciado entre platos y la tensión superficial. Fuente:
https://dx.doi.org/10.5772/57249
Tomando en consideración los efectos antes mencionados, el
factor K puede ser calculado (para platos de válvula y platos
perforados) usando la correlación de Kister y Hass:
2 0,144 ‹
K<
h
Û
É4
Ž
, O
‹
ÉÊ
É4
Ž
,
‹
Ü
ÝÞ
Ž
,O
(C)
Donde:
dH: diámetro del orificio, in

23. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
ρL: densidad del líquido, kg/m3
o lb/ft3
ρV: densidad del vapor, kg/m3
o lb/ft3
hc: altura del líquido claro, in
Figura 28. Factor K para copa de burbujeo. Fuente:
https://dx.doi.org/10.5772/57249
Utilizando datos adicionales de operación de columnas
comerciales, Fair (1961) consiguió una correlación más general
de la obtenida por Sourders y Brown, que es aplicable a platos
perforados, de válvulas y copas de burbujeo, como se muestra
en la Figura 29. En esta correlación, el valor del factor K es una
función del parámetro de flujo, Flv, espaciamiento entre platos,
tensión superficial y la fracción de área del orificio.
La velocidad de inundación, Uinun basada en el área neta de
flujo de vapor se determina mediante la ecuación:
¾ ÍUß,— ‹
Û
Ž
,
”
É4 ÉÊ
ÉÊ
, '/ (D)
Donde σ es la tensión superficial en dinas/cm y Csb,f es el factor
de capacidad y es una función del parámetro de flujo
d® dWX
à4
àÊ
”
ÉÊ
É4
(E)
Figura 29. Factor de capacidad de inundación de platos
perforados. Fuente: Wankat, P., 2008.
Donde WL y WV son los flujos másicos de líquido y vapor, y las
densidades son densidades másicas. La correlación Csb,f se
determina en la Figura 20. Wankat, P., (2008) menciona que
Kessler y Wankat, 1987 ajustaron a ecuaciones las curvas de la
Figura 20, mediante un análisis de regresión no lineal por
mínimos cuadrados; para alturas entre platos de 6 pulgadas:
t€áŒÖâã‡,§ −Œ, ŒÚÒÒ − Ö, ÓÐŒÔÐt€áŒÖ‰tä − Ö, Œ×ÒÑÖ t€áŒÖ‰tä*Ø
Para distancias entre platos de 9 pulgadas:
t€áŒÖâã‡,§ −Œ, ŒÑØØ − Ö, ÓÑÖŒÔt€áŒÖ‰tä − Ö, Œ×ŒÑ× t€áŒÖ‰tä*Ø
Para distancias entre platos de 12 pulgadas:
t€áŒÖâã‡,§ −Œ, ÖÑÒÔ − Ö, ÓÓÒ×Öt€áŒÖ‰tä − Ö, ŒÒÚŒÚ t€áŒÖ‰tä*Ø
Para distancias entre platos 18 pulgadas:
t€áŒÖâã‡,§ −Œ, ÖØÑØ − Ö, ÑÐÓŒÐt€áŒÖ‰tä − Ö, ØÖÖÚÒ t€áŒÖ‰tä*Ø
Para distancia entre platos de 24 pulgadas:
t€áŒÖâã‡,§ −Ö, ÚÔÓÖÑ − Ö, ÒÖØÐÔt€áŒÖ‰tä − Ö, ØØÑŒ× t€áŒÖ‰tä*Ø
Para distancias entre platos de 36 pulgadas:
t€áŒÖâã‡,§ −Ö, ×ÓÚ×Ô − Ö, ÒÐÚ×Öt€áŒÖ‰tä − Ö, ØÐÒÐÓ t€áŒÖ‰tä*Ø
En la correlación de inundación se supone que β, la relación del
área de los agujeros, Aaguj, entre el área activa del plato, Aactv,
es igual o mayor que 0,1. Si β < 0,1, se debe multiplicar la
velocidad de inundación calculada con la ecuación (11) por un
factor de corrección. Si,
β = 0,08 → factor de corrección es 0,9
β = 0,06 → factor de corrección es 0,8
Como puede observarse es una correlación lineal y se puede
interpolar con facilidad. El valor de la velocidad de inundación
es conservador (Wankat, P., 2008).
El espaciamiento entre platos, en la correlación de inundación
se selecciona de acuerdo con las necesidades de
mantenimiento. Los platos perforados tienen distancias entre
ellos de 6 a 36 pulgadas; de 12 a 16 pulgadas son los límites
comunes para torres pequeñas (menores de 5 ft). En general,
la altura entre platos es mayor en columnas de gran diámetro.
Se usa un mínimo de 18 pulgadas y 24 pulgadas por facilidad
de mantenimiento.
La velocidad de operación para el vapor se determina con:
QT "!((%ó&* ∗ ¾ '/ (F)
Donde la fracción puede ir de 0,65 a 0,90. Wankat, P (2008)
indica que Jones y Melbom (1982) sugieren usar siempre un
valor de 0,75 para esa fracción. Fracciones mayores de
inundación no afectan mucho el costo general del sistema,
pero si restringen la flexibilidad. La velocidad de operación se
puede relacionar con el flujo molar del vapor mediante la
ecuación:
QT
Çåå
æææææÊ
ÉÊ6kAš ȶ *
'/ (G)

24. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
El área neta para el flujo de vapor es
ç HS
Ì3h
Î
è ' (H)
Donde η es la fracción del área transversal de la columna
disponible para el flujo de vapor sobre el plato. Así, 1 – η es la
fracción del área de la columna ocupada por un bajante. El
valor característico de η está entre 0,85 y 0,95; este se puede
calcular con exactitud una vez finalizada la distribución del
plato. El diámetro de la columna se puede calcular a partir de
la ecuación (17),
_ ”
ÎÇ åå
æææææ[*
ÌéÉÊ —RLPP ó *¾>kêk ȶ *
(I)
Si es válida la ley de gas ideal,
ËÇ
åå
æææææÊ
³Ü
(J)
Y la ecuación (18) se transforma en:
_ ”
ÎdzÜ
Ìé ȶ * —RLPP ó *¾>kêk
' (K)
Los términos de las ecuaciones (13) a (20) varían de una etapa
a otra en la columna, por tanto si se hace el cálculo en distintos
puntos de la columna, se obtendrán distintos diámetros. Se
debe usar el diámetro máximo, redondeado hasta el
incremento de ½ ft más cercano, por ejemplo una columna de
9,14 ft se redondea a 9,5 ft. Ludwig (1997) y Kister (1990)
sugieren usar un diámetro mínimo de columna de 2,5 ft. Las
columnas con diámetros menores de 2,5 ft se suelen construir
como columnas empacadas. El cálculo del diámetro debe
hacerse en la parte superior e inferior de la columna y arriba y
debajo de la alimentación, en uno de esos lugares con mucha
aproximación se obtendrá el diámetro máximo y será
satisfactorio el diseño basado en el máximo diámetro
calculado (Wankat, P., 2008). Para columnas que trabajen a
presión atmosférica o mayores, la presión será esencialmente
constante en la columna. La relación entre las ecuaciones de
cálculo del diámetro en la parte superior e inferior de la
columna es como sigue:
wãë~
w§€s†€
•
ìãë~
지s†€
„
Œ
Ø
Z
•
ííì,ãë~
ííì,§€s†€
„
Œ
Ô
Z
•
îx,§€s†€
îx,ãë~
„
Œ
Ô
Z
•
Õãë~
Õ§€s†€
„
Œ
Ô
Z
•
Ù§€s†€
Ùãë~
„
Ö,Œ
•
âã‡,§,§€s†€
âã‡,§,ãë~
„
Œ
Ø
Z
Wankat, P., (2008), señala que si la alimentación es liquido
saturado y se destila una serie homologa, probablemente la
relación de diámetros es menor que 1,0 y que el termino
calculado para el fondo es mayor. Si la alimentación es un
vapor saturado, es probable que la relación de diámetros sea
mayor que 1,0 y se deba diseñar con las condiciones
superiores. Sin embargo, cuando se destila agua con una
sustancia orgánica y el agua es el producto destilado, así como
destilaciones criogénicas, la relación de diámetros podría ser
mayor o menor que 1,0.
Giménez, G. A (2003) presenta una correlación empírica
propuesta por Heaven que permite determinar en una forma
sencilla y aproximada el diámetro de la columna y la altura.
Dichas ecuaciones se muestran a continuación:
Diámetro de la columna, DC:
_ï Ÿ‹
Î
ÌÇ
Ž _* 0 + 1* 22,2* ‹
Ü9Ê
ðÈ
Ž ‹ Ž ‹
ȶ
Ž
Z
(L)
Donde: c 0,761 ‹ Ž
Z
(M)
DC: diámetro de la columna, m
D: Flujo de destilado, kmol/h
R: Relación de reflujo
TDV: Temperatura de rocío en el condensador, K
P: Presión de la columna, atm.
Altura de la columna, HC.
;ï 0,61 ‹
n
ñ›
Ž + 4,27 (N)
Donde:
N: Numero de etapas ideales
εo: Eficiencia global
Balance equilibrado del diámetro.
Ocasionalmente el diámetro calculado en diferentes puntos de
la columna puede variar por un gran factor, por ejemplo para
la destilación de una mezcla etanol-agua, si la alimentación es
vapor saturado, el diámetro calculado en el tope de la columna
es 3,7 veces mayor que el diámetro calculado en el fondo. Para
una destilación de una mezcla liquida de ácido acético-agua el
diámetro calculado en el fondo fue 1,7 veces el diámetro
calculado en el tope (Wankat, P., 2012).
En lugar de construir toda la columna con el diámetro más
grande, es posible equilibrar los diámetros de la columna. La
ecuación (20) muestra que el diámetro de la columna es
directamente proporcional a la raíz cuadrada de la velocidad
del vapor, V. Si se reduce V en la zona con mayor diámetro y se
aumenta V en cualquier otro punto de la columna, se puede
disminuir el diámetro de la columna significativamente con un
efecto muy pequeño sobre la pureza.
Si la condición termodinámica de la alimentación es vapor, el
diámetro de la columna suele ser mayor en la zona de
enriquecimiento. Se puede reducir el diámetro disminuyendo
V por condensación del vapor dentro de la columna con un
condensador intermedio. Tres métodos para hacer esto se
muestran en la Figura 30. En todos los casos habrá una
reducción en la pureza si L/D y N permanecen constantes. A
menudo, agregar algunas etapas restaurara la pureza al valor
deseado. Si los diámetros calculados tienen una marcada
diferencia, probablemente se reducirá el volumen neto de la
columna y el costo de la columna a pesar del uso de más
etapas. En la destilación de una mezcla de vapor de etanol-
agua, se logra una reducción en el volumen de la columna de

25. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
58% con la alimentación parcialmente vaporizada (Figura 31B)
y del 42% con un condensador intermedio con cargas
constante de calentamiento y enfriamiento. Enfriar toda la
alimentación (Figura 30A) podría reducir el volumen de
manera significativa, pero se tuvieron que aumentar el QC y el
QR (Wankat, P., 2012).
Figura 30. Métodos de balances de columnas para
alimentaciones de vapor con grandes diámetros calculados en
el tope, (A) alimentación enfriada completamente; (B)
enfriamiento parcial de la alimentación y (C) Condensador
intermedio. Fuente: Wankat, P., 2012.
Para un sistema de alimentación liquida con grandes
diámetros en la zona de agotamiento, se quiere reducir V en el
fondo de la columna e incrementar V en la parte superior de la
columna. El calor del rehervidor puede reducirse (V decrece) si
se calienta la alimentación (Figura 31A), o se vaporiza una
parte de la alimentación (Figura 31C), o se usa un rehervidor
intermedio (Figura 31D). Si el número de etapas y la relación
de reflujo son constantes, estos métodos tendrán baja pureza.
De nuevo, agregar algunas etapas resolverá esta dificultad.
Para la destilación de la mezcla ácido acético-agua con cargas
de calor constantes, una reducción del volumen de la columna
de 54% fue obtenida con un rehervidor intermedio (Figura 32),
con una derivación de vapor (Figura 31C) la reducción fue de
9,6%, vaporizando una parte de la alimentación (Figura 32B) la
reducción fue de 12% y calentando la alimentación (Figura
30A) la reducción fue del 10% (Wankat, P., 2012).
La adición de un intercambiador de calor y una etapa adicional
de alimentación (Figuras 30 A-B y 31A-B) son sencillos y no
deberían causar problemas de funcionamiento. Wankat, P.
(2012) indica que Sloley (1996) manifiesta que los
condensadores y rehervidores intermedios (Figura 30C y 32) se
usan comúnmente, sin embargo pueden hacer que la puesta
en marcha sea significativamente difícil. El mejor sistema se
puede determinar usando los paquetes de simulación (PRO II,
ASPEN, HYSYS, entre otros).
A pesar que en el diseño de un plato se cumpla con las
especificaciones y se tengan en cuenta todas las limitantes
hidráulicas, es posible que se presenten serias dificultades si se
producen cambios drásticos durante su operación (por
ejemplo, un cambio súbito de mínima a máxima capacidad). Se
ha encontrado que es posible disminuir la ocurrencia de tales
contratiempos con lo que se denomina diseño balanceado del
plato, que se soporta en ciertos valores de parámetros
específicos, los cuales corresponden a porcentajes de valores
considerados máximos permisibles, respecto a los siguientes
parámetros; velocidad del gas en condiciones de inundación
por arrastre, llenado del bajante y velocidad de entrada en el
canal de descenso. Estos valores deben permanecer cercanos
(o iguales, de ser posible) a los recomendados y usualmente
varían entre 80 y 85% de los máximos.
Figura 31. Métodos de equilibrio de columnas para
alimentaciones liquidas con grandes diámetros calculados en
el fondo, (A) calentando la alimentación, (B) vaporizando parte
de la alimentación y (C) con una derivación del vapor. Fuente:
Wankat, P., 2012
Figura 32. Uso de un rehervidor intermedio. Fuente: Wankat,
P., 2012
Factores limitantes de la capacidad en columnas de
destilación.
La capacidad se refiere a la cantidad de flujo de vapor y líquido
que pueden manejar los internos de una torre (platos o
empaques), manteniendo una eficiencia estable. Cuando
estos varían con respecto al flujo normal de operación la
capacidad puede verse afectada por los siguientes factores:
inundación, arrastre de líquido, formación de espuma, llenado
excesivo del bajante y goteo o lagrimeo.
Para garantizar una operación satisfactoria, a un diámetro
dado, debe utilizarse una velocidad de vapor inferior al 90% del

26. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
límite de operabilidad, de no ser posible debe aumentarse el
diámetro de la columna. Como la inundación y el goteo
determinan los límites de operación de una columna de
destilación es conveniente conseguir los valores mínimos y
máximos del área perforada en el plato para que el área
perforada efectiva sea tal que permita una buena operabilidad
de la columna.
Un plato de fraccionamiento debe operarse dentro de un
rango de flujo de vapor y líquidos para obtener un
comportamiento óptimo. Fuera de este rango, la eficiencia es
baja y/o la torre esta inoperante. Entre estas consideraciones
básicas de diseño se tiene la capacidad máxima y la flexibilidad
operacional, que serán descritas a continuación.
Capacidad máxima.
La capacidad máxima de vapor que la torre puede manejar, la
cual depende principalmente de las propiedades del sistema.
La carga de vapor no se puede incrementar por cambios en el
diseño del plato o aumentos en el espaciamiento entre platos,
sino solamente por aumentos en el área libre de la torre.
(PDVSA, 1996).
Cargas máxima.
Flujo máximo de vapor. Una velocidad de vapor demasiado alta
a través de los orificios del plato y/o través del área libre de la
torre puede causar:
• Arrastre o inundación por chorro
• Altas caídas de presión a través del plato, causando un
llenado excesivo del bajante y por consiguiente inundación
del plato.
• Dependiendo de las propiedades del sistema (densidad del
vapor y líquido y tensión superficial del líquido), flujos de
vapores mayores a la llamada capacidad máxima,
atomizara el líquido y lo arrastrara hacia arriba
dependiendo de la geometría y el espaciamiento entre
platos.
Flujo máximo de líquido. Flujos excesivos de líquido pueden
causar:
• Inundación del plato debido a la segregación insuficiente
en los bajantes, excesiva caída de presión en el plato y
excesivo llenado del bajante.
• Goteo o vaciado a bajos flujos de vapor.
• Altos gradientes de líquidos, los cuales originan mala
distribución del vapor y una pobre eficiencia de contacto
(plato tipo de copas de burbujeo).
Cargas mínimas.
Flujo mínimo de vapor. Un flujo de vapor demasiado bajo
puede causar:
• Goteo o vaciado a flujos altos de líquido.
• Pobre contacto y baja eficiencia del plato debido al
mezclado inadecuado de vapor/líquido.
Flujo mínimo de líquido. Un flujo bajo de líquido puede causar:
• Arrastre a altos flujos de vapor.
• Desvío del vapor ascendente por el bajante, en caso de que
la altura del líquido claro sobre el plato, más la perdida de
cabezal en el bajante, no sean iguales o mayores que el
espacio libre en el bajante a flujo mínimo.
• Pobre contacto y baja eficiencia, debido a un líquido
inadecuado en el plato.
Por otra parte, a medida que las cargas se reducen, se llega a
un punto en el cual el equipo de contacto ya no es efectivo para
proporcionar un buen contacto entre las dos fases. Cada tipo
de plato se caracteriza por un grupo diferente de flujos por
debajo de los cuales no operara satisfactoriamente. En el caso
de platos perforados de flujo transversal, la reducción de la
carga de gas más allá de un cierto valor causa un
derramamiento y vaciado excesivo de líquido, lo que reduce la
dispersión del vapor dentro de la fase liquida. Con la
dispersión reducida, sobreviene una reducción en el área
interfacial, lo cual a su vez reduce la velocidad de transferencia
de masa entre las fases. Los platos de válvula se pueden operar
a cargas de vapor relativamente bajos, ya que la abertura de
la válvula cierra a medida que la carga de líquido disminuye.
Los platos de copas de burbujeo puede operar a cargas de gas
muy bajas debido a su arreglo de sellado (Holland, Ch., 2000)
Una forma práctica d evaluar el desempeño de un plato es
mediante los diagramas de estabilidad. Éstos relacionan en
una gráfica las condiciones límite de operación de cada tipo
de plato, estableciendo un área óptima de operación. De
este modo, con las cargas de líquido y vapor, es posible
determinar si un plato está operando bajo condición
estable o está presente alguno(s) de los fenómenos de
inestabilidad (Carrasquero, Y., 2018, p.40).
En la Figura 33 se muestra un diagrama típico de estabilidad de
los platos perforados o zona de operación segura. En él se
observan las curvas de inundación, goteo y las derivaciones de
cada una, así como las condiciones de arrastre de líquido y
mala distribución de las fases.
Flexibilidad operacional (turndown ratio).
La flexibilidad de un plato se define como su capacidad de
mantener condiciones de operación estables incluso cuando el
flujo de alimentación sea inferior al flujo de diseño y cuando se
presentan fluctuaciones en el alimento. Como consecuencia, el
diseño del plato se basa en sus condiciones extremas de
operación, asociadas a los fenómenos de lloriqueo y arrastres
tolerables.
También puede definirse, como la relación entre la carga de
vapor en operación normal (o diseño) y la carga de vapor
mínima permitida. La mínima carga permitida generalmente
está separada con un margen de seguridad del límite donde la
inundación comienza a ser relevante. Esta da a la columna un
rango de operación que asegura un funcionamiento

27. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
satisfactorio de los platos y por ende la calidad de los
productos.
||||||||||||||||||||||||||||||||||||
Figura 33. Diagrama de estabilidad para platos perforados.
Fuente: Carrasquero, Y., 2018.
Si se modifica (incrementa) la caída de presión a través de los
orificios de un plato perforado, puede aumentarse su
flexibilidad hasta hacerla comparable con la de algunos platos
de válvula. Otra manera de lograr flexibilidades elevadas
consiste en diseñar el plato con un alto número de
perforaciones y tapar provisionalmente un porcentaje, de
manera que se cuenta con una gran variedad de valores de
área perforada a disposición del usuario.
En columnas de múltiples pasos se logra mayor flexibilidad
entre mejor balanceados estén los pasos, es decir, en la
medida en que la caída de presión por paso sea igual a la caída
de presión global.
Es usual manejar flexibilidades de 70-80% (2:1) y 40-50%
(1,25:1) en platos perforados, en operaciones a presión
atmosférica y a vacío, respectivamente. Si se desean
flexibilidades mayores, debe pensarse el uso de válvulas o
copas de burbujeo (Bernal B., D. y col. 1990).
Procedimientos de solución rigurosas para sistemas
multicomponente.
La utilización de computadores digitales ha hecho que la
solución rigurosa de las ecuaciones MESH sea una propuesta
práctica, y los métodos informáticos para el diseño de
columnas de destilación multicomponente estén disponibles
en la mayoría de las organizaciones de diseño. Se han realizado
una cantidad considerable de trabajos durante los últimos
veinte años para desarrollar procedimientos de diseño
asistidos por computadoras eficientes y confiables para
destilaciones y otros procesos por etapas.
Características de la alimentación.
El tamaño de una columna de destilación es definido
principalmente en términos relacionados por las
características de la alimentación y la especificación de los
productos deseados.
Se refiere principalmente a:
• Al flujo de alimentación del equipo que naturalmente
gobierna el tamaño requerido del equipo.
• La composición de la alimentación que puede darse
por constituyente para el caso del análisis una mezcla
de constituyentes conocidos o identificados, o
también en forma de análisis TBP en el caso de crudos
y cortes de petróleo.
• En función de los métodos de diseño utilizados, a
veces puede ser necesario reducir el número de
constituyentes a analizar para reducir la complejidad
de las operaciones a realizar. En este caso lo práctico
es agrupar los componentes con volatilidades
similares.
• La temperatura de la alimentación y su presión
determinan el flujo de calor correspondiente al
proceso y las condiciones de vaporización en la
entrada de la columna.
• La entalpia puede determinarse por las condiciones
de temperatura y presión a la que se suministra la
alimentación. También puede depender del calor
recuperado por el intercambio de calor entre la
alimentación y el producto de fondo.
• En algunos casos, será necesario precalentar o enfriar
la alimentación para alcanzar las condiciones
especificadas.
• En términos generales, la alimentación debería estar
al menos en su punto de ebullición, a la presión de
operación al ingresar a la columna. Eventualmente,
una alimentación subenfriado (o vapor
sobrecalentado) ocasiona intercambios de calor que
podrían ser perjudiciales dentro de la columna.
• Estos datos aplican a más de una alimentación
restringida a una alimentación, por lo que la columna
de destilación debe ser diseñada para procesar dos o
más alimentaciones con diferentes velocidades de
flujo, composiciones y temperaturas.
Referencias Bibliográficas.
• Henley, E. J., Seader, J. D. y Keith Roper, D. (2010).
Separations Process principles: chemical and biochemical
operations. Tercera edición. Editorial John Wiley & Sons,
Inc.
A
rr
a
s
tr
e
e
x
c
e
s
iv
o
Carga
de
vapor

28. Fraccionamiento-Mezclas Multicomponente
Facilitador: Ing. Zoraida J. Carrasquero MSc. 2022
• Wankat, P. C. (2012). Separations Process Engineering:
include mass transfer analysis. Tercera edición. Editorial
Pearson Education, Inc.
• Henley, E. J. y Seader, J. D. (1998). Operaciones de
Separación por etapas de equilibrio en ingeniería química.
Segunda Edición. Editorial Reverté, S. A.
• Wankat, P. C. (2008). Ingeniería de Procesos de Separación.
Segunda Edición. Editorial Pearson Educación de México S.
A.
• Treybal, R. E. (1981). Operaciones de Transferencia de
Masa. Segunda edición. McGraw-Hill de México, S.A. de C.
V.
• King, J, C. (1979). Procesos de Separación. Edición en
español. Editorial Reverté S.A.
• McCabe, W. l., Smith, J. C. y Harriott, P. (2007). Operaciones
Unitarias en Ingeniería Química. Séptima edición. McGraw-
Hill/Interamericana Editores, S. A. de C. V.
• Kister, H. Z. (1992). Distillation Design. Editorial McGraw-
Hill
• Hines, A. L. y Maddox, R. N. (1985). Mass Transfer.
Fundamentals and Applications. Editorial Prentice- Hall
PTR.
• Ocon G., J. y Tojo B., G. (1980). Problemas de Ingeniería
Química. Operaciones básicas. Tomo I. Quinta reimpresión.
Colección Ciencia y Técnica-Aguilar.
• Foust, A. S., Wenzel, L. a., Clump, C. W., Maus, L. y Bryce
Andersen, L. (2006). Principios de Operaciones Unitarias.
Decima reimpresión. Editorial CECSA. Versión en digital.
• Ludwig, E. E. (1994). Applied process design for chemical
and petrochemical. Tomo 2. Tercera edición. Gulf
Professional Publishing Editores. Versión en digital.
• Martínez de la Cuesta, P. y Rus Martínez, E. (2004).
Operaciones de Separación en Ingeniería Química. Métodos
de Cálculo. Editorial Pearson-Prentice-Hall.
• Kiss, A. A. (2013). Advanced Distillations Technologies.
Desing, Control and applications. John Wiley and Sons Ltd.
Publications. Versión en digital.
• Geankoplis, C. J. (1998). Procesos de Transporte y
Operaciones Unitarias. Tercera edición. Editorial CECSA de
C.V.
• Sinnot, R. K. (2005). Chemical Engineering Design. Tomo 6.
Cuarta edición. Coulson & Richardson’s. Chemical
Engineering Series.
• Jiménez G., A. (2003). Diseño de Procesos en Ingeniería
Química. Editorial Reverté. Versión en digital.
• Holland, Ch. D. (2000) Fundamentos de Destilación de
mezclas multicomponente. Segunda reimpresión. Editorial
LIMUSA, S. A. de C. V.
• Branan, C. R. (2000) Soluciones Prácticas para el Ingeniero
Químico. Segunda Edición. McGraw-Hill Interamericana
Editores, S. A. de C. V.
• Marcilla G., A. (1998). Introducción a las operaciones de
Separación. Calculo por etapas de equilibrio. Edición
electrónica: Espagrafic. Publicaciones de la Universidad de
Alicante.
• Prieve, D. C. (2000) Unit Operations of Chemical
Engineering. Class Notes. Elecronic version in PDF.
Department of Chemical Engineering. Carnegie Mellon
University, Spring 2000.
• Bernal B., Daniel; Castellano D, Orlando; Bejarano J, Pedro
y Rodríguez N., Gerardo. (1990). Análisis y diseño de platos
y columnas de platos. Editorial Tecni-Ciencia.
• http://iq.ua.es/MetAprox/411_clculo_del_nmero_mnimo
_de_etapas.html) Revisado el 02/02/2018.
• Hassan Al-Haj Ibrahim. Desing of Fractionation Columns.
Chapter 5. Tomado de: http://dx.doi.org/10.5772/57249.
• Thirumalesh, B. S. y Ramesh, V. (2015), Case study on
multicomponent distillation and distillation column
sequencing. INTERNATIONAL JOURNAL OF ENGINEERING
SCIENCES & RESEARCH TECHNOLOGY. 4(8): AUGUST 2015.
Tomado de http://www.ijesrt.com. Revisado el
02/02/2018.
• Carrasquero, Y. (2018). Evaluación técnica de la capacidad
nominal de la unidad de destilación atmosférica No. 3 del
CRP Cardón. (Tesis de pregrado inédita). UNEFM. Programa
de Ingeniería Química. Falcón-Venezuela.