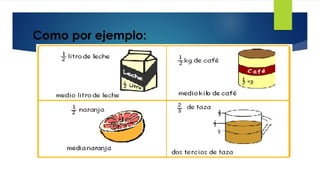
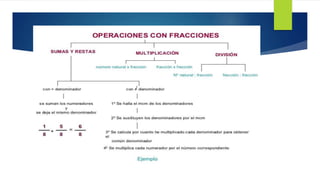
El documento describe la historia y conceptos básicos de las fracciones. Los egipcios fueron los primeros en usar fracciones en el 2000 a.C., representándolas como sumas de fracciones unitarias. Una fracción representa una parte de un todo y consta de un numerador y un denominador. Existen diferentes tipos de fracciones como las de términos enteros y las operaciones básicas con ellas como suma, resta, multiplicación y división.

2. Historia acerca de los números
fraccionarios
 El primer conocimiento acerca de las fracciones se produce en el año 2000 a.C. en
Egipto, aunque los egipcios solamente las utilizaban como divisores de la unidad y
sus métodos de calculo eran mucho mas complicados que los nuestros actuales .
 La base de la representación de una fracción se encontraba en la descomposición
como suma de fracciones de numerador 1, todas distintas . En la representación de
fracciones, se empleaba el símbolo que significaba “ Partes” . Cuando se
quería escribir un valor fraccionario se representaba el símbolo anterior seguido por
el valor numérico del denominador.
 Ejemplo:
5

3. Las fracciones
 Una fracción es un numero con el que expresamos una parte de algo.

4. Como por ejemplo:

5. La unidad fraccionaria es cada una de las partes que se obtienen al
dividir la unidad en n partes iguales.
concepto de fracción
Una fracción es el cociente de dos números enteros a y b, que representamos de
la siguiente forma:

6. Muy importante:
 b se llama denominador de la fracción , y nos indica en cuantas partes
se divide la unidad. El denominador nunca puede ser 0 “ cero”.
 a se llama numerador de la fracción , y nos indica cuantas partes
tomamos.
Un depósito contiene 2/3 de gasolina
El todo es el depósito.
La unidad equivale a 3/3, en este caso.
En general, el todo sería una fracción con el mismo número
en el numerador y el denominador de la forma n/n.

7. Lectura de fracciones
 Las fracciones tienen una forma especial de leerse dependiendo del
valor que tenga el denominador ; así, si el denominador es un numero
comprendido entre 2 y 10, se lee el numerador seguido del ordinal del
denominador.
 Si el denominador es un numero mayor que 10, se lee el numerador
seguido del denominador con la terminación avo.
10
6 se lee diez sextos
14
56 se lee catorce cincuenta y seisavos

8. Ejemplos:

9. TIPOS DE FRACCIONES

10. Muy importante

11. FRACCIONES DE TERMINOS ENTEROS
 En cada una de las siguientes fracciones , el numerador y el
denominador son números enteros negativos o positivos.
 Por ello, las llamamos fracciones de términos enteros.
-2 , 3 , -1 , -9 , 4
5 4 3 -2 7

12. Recuerda que una fracción puede ser:
Fracción positiva
 Una fracción es positiva si el
numerador y el denominador tienen el
mismo signo.
Fracción negativa
 Una fracción es negativa si el
numerador y el denominador tienen
distinto signo.
- 15 15
8 8
- 5 5
- 7 7

13. SIMPLIFICACION DE FRACCIONES
 Se puede formar una fracción equivalente a :
 Reduciendo la fracción a una fracción equivalente
a multiplicando a y b un mismo número , o dividiendo
b a y b, por un mismo número distinto de cero.

14. EJEMPLOS:
 Multiplicando a una fracción por un mismo numero.
 Dividiendo a una fracción por un mismo numero.

16. OPERACIONES CON NUMEROS
RACIONALES
 Suma y resta cuando la fracción tiene el mismo denominador:
 Para sumar o restar fracciones con el mismo denominador , se suman o restan los numeradores,
y el signo lleva del numero mayor y se mantiene el denominador.

17. Ejemplo:

18. Para sumar o restar fracciones con distinto denominador, tendremos que
transformarlas en otras equivalentes con el mismo denominador.

19. Multiplicación y división:
El producto de dos fracciones es otra
fracción cuyo denominadores y cuyo
numerador es el producto de sus
numeradores.
La división de dos fracciones es la
multiplicación de la primera por la
inversa de la segunda.