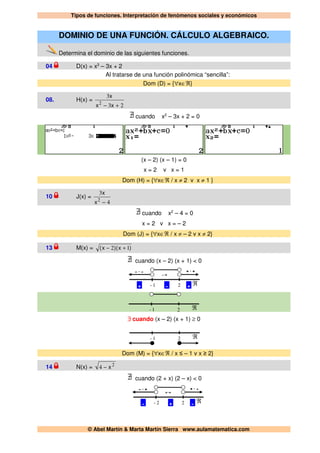
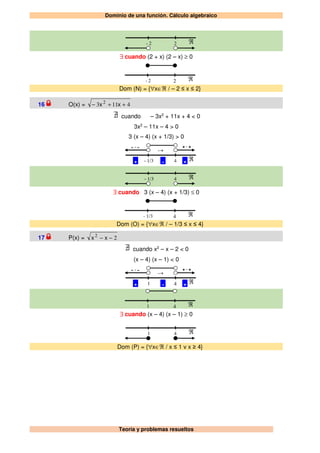
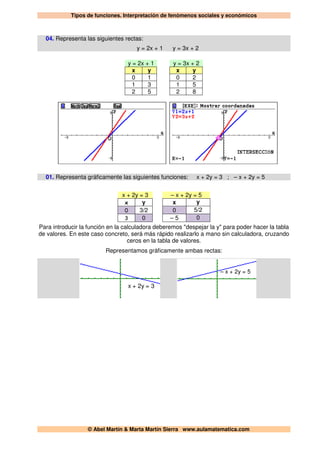
Este documento describe los dominios de varias funciones. Explica cómo determinar el dominio analizando si la función es polinómica o racional y resolviendo las ecuaciones que surgen de los denominadores. Proporciona ejemplos detallados del cálculo del dominio para funciones como D(x), H(x), J(x), M(x), N(x), O(x) y P(x). También incluye instrucciones para representar gráficamente rectas y funciones lineales.

1. Tipos de funciones. Interpretación de fenómenos sociales y económicos
© Abel Martín & Marta Martín Sierra www.aulamatematica.com
DOMINIO DE UNA FUNCIÓN. CÁLCULO ALGEBRAICO.
Determina el dominio de las siguientes funciones.
04 D(x) = x3
– 3x + 2
Al tratarse de una función polinómica “sencilla”:
Dom (D) = {∀x∈ℜ}
08. H(x) =
23
3
2
+− xx
x
∃/ cuando x2
– 3x + 2 = 0
(x – 2) (x – 1) = 0
x = 2 v x = 1
Dom (H) = {∀x∈ℜ / x ≠ 2 v x ≠ 1 }
10 J(x) =
4
3
2
−x
x
∃/ cuando x2
– 4 = 0
x = 2 v x = – 2
Dom (J) = {∀x∈ℜ / x ≠ – 2 v x ≠ 2}
13 M(x) = )x)(x( 12 +−
∃/ cuando (x – 2) (x + 1) < 0
- 1 ℜ2
-·- +·+
-·+
+ - +
- 1 ℜ2
∃ cuando (x – 2) (x + 1) ≥ 0
- 1 ℜ2
Dom (M) = {∀x∈ℜ / x ≤ – 1 v x ≥ 2}
14 N(x) = 2
4 x−
∃/ cuando (2 + x) (2 – x) < 0
- 2 ℜ2
-·+ +·-
+·+
- + -

2. Dominio de una función. Cálculo algebraico
Teoría y problemas resueltos
- 2 ℜ2
∃ cuando (2 + x) (2 – x) ≥ 0
- 2 ℜ2
Dom (N) = {∀x∈ℜ / – 2 ≤ x ≤ 2}
16 O(x) = 4113 2
++− xx
∃/ cuando – 3x2
+ 11x + 4 < 0
3x2
– 11x – 4 > 0
3 (x – 4) (x + 1/3) > 0
- 1/3 ℜ4
-·- +·+
-·+
+ - +
- 1/3 ℜ4
∃ cuando 3 (x – 4) (x + 1/3) ≤ 0
- 1/3 ℜ4
Dom (O) = {∀x∈ℜ / – 1/3 ≤ x ≤ 4}
17 P(x) = 22
−− xx
∃/ cuando x2
– x – 2 < 0
(x – 4) (x – 1) < 0
1 ℜ4
-·- +·+
-·+
+ - +
1 ℜ4
∃ cuando (x – 4) (x – 1) ≥ 0
1 ℜ4
Dom (P) = {∀x∈ℜ / x ≤ 1 v x ≥ 4}

3. Tipos de funciones. Interpretación de fenómenos sociales y económicos
© Abel Martín & Marta Martín Sierra www.aulamatematica.com
04. Representa las siguientes rectas:
y = 2x + 1 y = 3x + 2
y = 2x + 1 y = 3x + 2
x y x y
0 1 0 2
1 3 1 5
2 5 2 8
01. Representa gráficamente las siguientes funciones: x + 2y = 3 ; – x + 2y = 5
x + 2y = 3 – x + 2y = 5
x y x y
0 3/2 0 5/2
3 0 – 5 0
Para introducir la función en la calculadora deberemos "despejar la y" para poder hacer la tabla
de valores. En este caso concreto, será más rápido realizarlo a mano sin calculadora, cruzando
ceros en la tabla de valores.
Representamos gráficamente ambas rectas:
x + 2y = 3
– x + 2y = 5