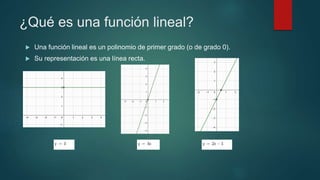
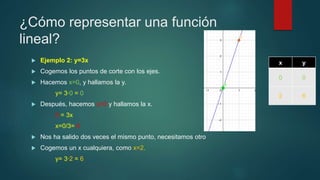
Una función lineal es un polinomio de primer grado cuya representación es una línea recta. Puede ser de tres tipos: constante, de proporcionalidad directa o afín. Se representa como y=mx+n, donde m es la pendiente y n la ordenada en el origen. Su dominio es R y su imagen depende de si m es distinto o igual a cero. Son continuas, pueden ser crecientes, decrecientes o constantes, y no son cóncavas, convexas ni periódicas.

1. Funciones lineales
RAFAEL MERELO GUERVÓS
IES SANTÍSIMA TRINIDAD

2. ¿Qué es una función lineal?
 Una función lineal es un polinomio de primer grado (o de grado 0).
 Su representación es una línea recta.

3. ¿Cómo es una función lineal en la vida
real?
 Pueden ser de tres tipos:
 Funciones que siempre tienen el mismo valor. Ejemplo: Coste del
teléfono si tenemos tarifa plana; y=3
 Funciones de proporcionalidad directa. Ejemplo: Coste de la compra de
aguacates, si el kilo vale a 3€. y=3x
 Funciones afines, con una cantidad fija y otra que depende de la x.
Ejemplo: Coste de la llamada si por descolgar cobran 3 céntimos, y
por minuto 2 céntimos; y=2x+3

4. ¿Cómo es una función lineal? en la
vida real?
 y=mx + n
 A m le llamamos pendiente. Cuánto más alta sea, la función crecerá más rápidamente.
Si es negativa, la función decrecerá. Si es 0, la función será constante (siempre el
mismo valor)
 A n le llamamos ordenada en el origen. Es el valor de la función en x=0, es decir, el
punto de corte con el eje y.
 Si m =0, a la función la llamamos constante.
 Si n =0, la función es de proporcionalidad directa.
 Si ni m ni n son 0, la llamamos afín.

5. ¿Cómo representar una función
lineal?
 Para representar una recta, basta con dos
puntos.
 Cogemos los puntos de corte con los ejes.
 Hacemos x=0, y hallamos la y.
 Después, hacemos y=0 y hallamos la x.
 Si necesitamos otro punto más (lo que pasará si m o
n son cero), cogemos uno cualquiera, como x=2, y
hallamos la y.

6. ¿Cómo representar una función
lineal?
 Ejemplo 1: y=3x-5.
 Cogemos los puntos de corte con los ejes.
 Hacemos x=0, y hallamos la y. y= 3∙0 – 5 = -5
 Después, hacemos y=0 y hallamos la x.
0 = 3x – 5
x = 5/3 = 1.666…
x y
0 -5
1,666 0

7. ¿Cómo representar una función
lineal?
 Ejemplo 2: y=3x
 Cogemos los puntos de corte con los ejes.
 Hacemos x=0, y hallamos la y.
y= 3∙0 = 0
 Después, hacemos y=0 y hallamos la x.
0 = 3x
x=0/3= 0
 Nos ha salido dos veces el mismo punto, necesitamos otro
 Cogemos un x cualquiera, como x=2.
y= 3∙2 = 6
x y
0 0
2 6

8. ¿Cómo representar una función
lineal?
 Ejemplo 3: y=3
 Cogemos los puntos de corte con los ejes.
 La función siempre vale 3, sea la x la que
sea.
 Cogemos dos puntos cualesquiera, uno de
ellos con x=0
x y
0 3
2 3

9. Características de una función lineal
 Dominio:
 Imagen: si m≠0,
 Imagen si m=0: {n}, por ejemplo, en la función y=5, la imagen es {5}, es
decir su imagen es sólo el número 5.
 Monotonía. Crecimiento y decrecimiento
 Siempre creciente si m>0
 Siempre decreciente si m<0
 Constante si x=0
 Continuidad: son continuas en

10. Características de una función lineal
 Curvatura: No son cóncavas ni convexas, son rectas.
 Simetría: si m=0 son pares , (son un polinomio que solo
tiene grado 0). Ejemplo: y=5
 Si n=0, son impares (son un polinomio que solo tiene
grado 1). Ejemplo: y=3x
 Periodicidad: No son periódicas.