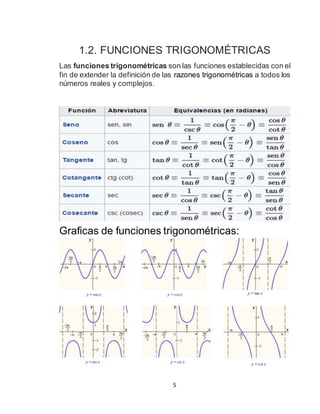
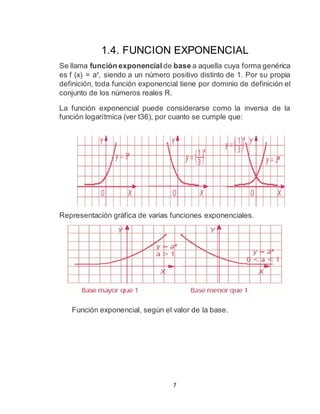
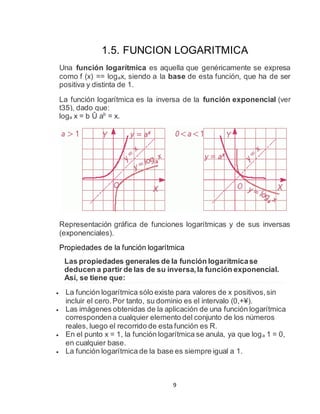
Este documento describe las funciones trascendentes como funciones que no satisfacen ecuaciones polinómicas. Cubre las funciones trigonométricas, inversas, exponenciales y logarítmicas, incluyendo sus definiciones, gráficas y propiedades. También explica cómo resolver ecuaciones y sistemas de ecuaciones que involucran funciones logarítmicas y exponenciales.