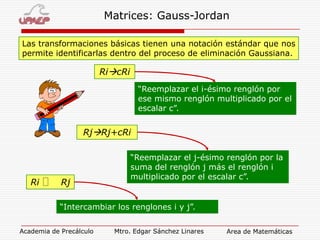
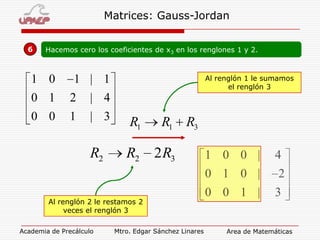
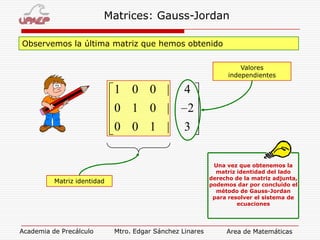
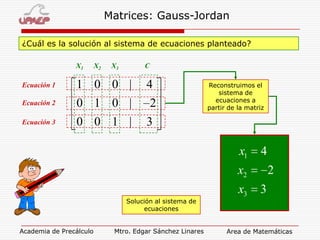
El documento explica el método de Gauss-Jordan para resolver sistemas de ecuaciones, el cual involucra escribir la matriz aumentada del sistema, aplicar transformaciones básicas a la matriz para obtener una matriz identidad en el lado izquierdo, y luego usar esta matriz para determinar la solución del sistema.