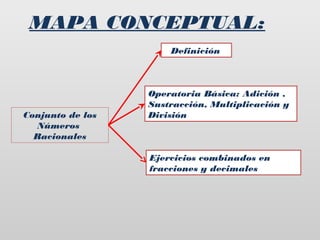
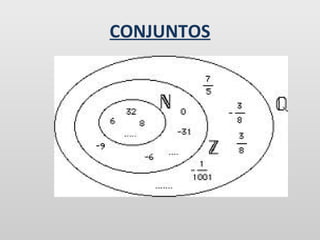
Este documento trata sobre los números racionales. Explica cómo representarlos como fracciones o decimales, y cómo realizar operaciones básicas y combinadas con ellos. Incluye definiciones de los números racionales, transformaciones entre fracciones y decimales, y ejemplos de suma, resta, multiplicación, división y operaciones combinadas con números racionales expresados como fracciones o decimales. El objetivo es que los estudiantes comprendan y puedan trabajar con los números racionales.

1. NIVELACIÓN
MATEMÁTICA
2014
1
ad
n id r o s
U
me les
Nú na
a ci o
R

2. OPERATORIA DE
LOS NÚMEROS
RACIONALES

3. MAPA CONCEPTUAL:
Definición
Conjunto de los
Números
Racionales
Operatoria Básica: Adición ,
Sustracción, Multiplicación y
División
Ejercicios combinados en
fracciones y decimales

4. OBJETIVOS
• Resolver problemas que involucren operatoria básica con los
números racionales.
•Reconocer y caracterizar los desarrollos en números
racionales.
• Representar intuitivamente números en la recta real.
• Reconocer las propiedades de las operaciones en el conjunto
de los números racionales
•Comprender que la ampliación del conjunto de los números
racionales obedece siempre a la necesidad de dar solución a
otro tipo de problemáticas.

5. Conjunto de los Números Racionales
El conjunto de los Números Racionales
se ha construido a partir del conjunto de los
Números Enteros. Se expresa por
comprensión como:
Se denota con la letra Q
a

Q =  / a, b ∈ Z ; b ≠ 0
b


6. Representación en la recta numérica
Cada fracción es un número racional y cada
número racional consta de infinitas
fracciones equivalentes, además cada
fracción puede ser denotada a la vez por un
número decimal.

7. OPERATORIA
El conjunto Q aparentemente permite
realizar todas las operaciones aritméticas.
Sin embargo, esto no es del todo efectivo,
ya que existen inconvenientes para realizar
algunas operaciones que ya conocerás. Se
hace necesario, entonces, seguir
construyendo otros conjuntos numéricos

8. DESTAQUEMOS
1)
a (numerador)
b (denominador)
2) La división por 0 no existe
3) El conjunto Q es denso. Esto significa que
dados dos números racionales, y por muy
pequeñas que sea su diferencia, entre ellos
hay infinitos números racionales.

9. CONJUNTOS

10. Números Racionales Expresados en
forma Decimal
• Para expresar un número racional, del tipo
a
, b ≠ 0 en forma decimal, basta dividir el
b
numerador por el denominador. Así
obtenemos tres tipos de números
Decimales: decimales finitos, decimales
infinitos periódicos y decimales infinitos
semiperiódicos.

11. TRANFORMACIÓN
DECIMALES FINITOS
Se caracterizan por tener una cantidad finita de dígitos
después de la coma decimal, hacia la derecha.
45 : 5
9
0, 045 =
=
1000 : 5 200
12 : 2 6
1, 2 =
=
10 : 2 5

12. TRANSFORMACIÓN DECIMALES
INFINITOS PERIÓDICOS
Se caracterizan por tener uno o más dígitos que se repiten
infinitamente en el mismo orden, inmediatamente después de la
coma decimal hacia la derecha. La cifra que se repite se
denomina período.
5718 − 57 5661: 9 629
57,18 =
=
=
99
99 : 9
11

13. TRANSFORMACIÓN DECIMALES
INFINITOS SEMIPERIÓDICOS
Se caracterizan por tener una o más cifras antes del período, que
forman lo que denomina el anteperíodo.
246 − 24 222 : 6
2, 466... = 2, 46 =
=
90
90 : 6
37
=
15
7
=2
15

14. Actividad 1
Transformar cada fracción en el decimal correspondiente y cada
decimal en su fracción correspondiente
a)
c)
e)
32
=
15
b)
33,56
d)
13, 7
f)
0, 45
12
=
99
78
=
45

15. Adición y sustracción en los números
racionales
a) Suma y resta de fracciones de igual
denominador: Para sumar o restar fracciones
de igual denominador se debe conservar el
denominador y sumar o restar
los
numeradores, dependiendo del operador, es
decir,
a c a+c
+ =
b b
b
a c a−c
− =
b b
b

16. • b) Adición y sustracción de números racionales de
distinto denominador.
• 1° encontrar el mínimo común múltiplo entre los
denominadores, que sería el denominador de la
fracción
• 2° para calcular el numerador divides el m.c.m. con el
denominador de la primera fracción y lo multiplicas
por el numerador de la misma.
• 3° Sumas o restas según el operador
• 4° repites el paso 2 para la segunda fracción
• 5° simplificar si es posible

17. 3 1
+ =
4 3
Ejemplo
Calculamos el m.c.m. entre 4 y 3 que es 12
3 1 3 ×3 + 4 ×1
+ =
4 3
12
3 1 9 + 4 13
+ =
=
4 3 12 12

18. Adición y sustracción en los números
racionales
c) Suma y resta de decimales: Para sumar o
restar decimales debemos alinear las comas,
así sumaremos y restaremos las partes
decimales del número y las partes enteras , es
decir:
7,37
+12, 003
19,373
27, 009
−17,994
10, 015

19. Actividad 2
• Resuelva las siguientes adiciones y sustracciones
de fracciones.
a)
c)
e)
5 4
+ =
4 4
b)
2 4
+ =
3 3
3 1
− =
5 5
5 3
+ =
5 2
d)
3 1
+ =
6 2
3 1
− =
6 2
f)

20. Actividad 3
• Resuelva las siguientes adiciones y sustracciones
de decimales.
a)
12, 75 + 0, 778 =
b)
33,99 + 0,345 =
c)
56, 004 − 7, 98 =
d)
6, 43 + 40, 78 =
e)
6, 7 +12, 78 =
f)
0,98 −12,345 =

21. Multiplicación de fracciones
• Para multiplicar facciones se deben multiplicar
los numeradores y el resultado será el nuevo
numerador y luego los denominadores se
multiplicarán para tener el nuevo
denominador. Se debe simplificar si es
posible.
a c a ×c
× =
b d b ×d

22. Ejemplo
3 5 3 × 15
5
× =
=
4 7 4 ×7 28
8 3 8 × 24
3
× =
=
7 5 7 × 35
5

23. Multiplicación de decimales
• Para multiplicar decimales se debe multiplicar sin considerar
las comas y luego en el resultado obtenido debemos
considerar como decimales una cantidad igual a la suma de
decimales entre los factores que multiplicamos.
• En el caso de multiplicar decimales infinitos, ya sean
periódicos o semiperiódicos debemos tranformarlos en su
fracción correspondiente y luego efectuar la operatoria

24. Ejemplo
0, 74 × 3 = 074 ×
12,
123 = 9102 = 9,102
112 − 11 3 101 1 101
1,12 ×0,3 =
× =
× =
= 0,3740
90
9 90 3 270

25. División de fracciones
• Para dividir fracciones se debe multiplicar por
el inverso multiplicativo de la segunda
fracción (invertir la segunda fracción).
a c a ×d
: =
b d b ×c

26. Ejemplo
3 5 3 ×7 21
: =
=
4 7 4 × 45
5
8 3 8 × 40
5
: =
=
7 5 7 × 21
3

27. División de decimales
• Para dividir decimales tenemos tres casos:
a) ENTERO:DECIMAL
O
DECIMAL:ENTERO
b) DECIMAL:DECIMAL
(IGUAL CANTIDAD DE
DECIMALES)
c) DECIMAL:DECIMAL
(DISTINTA CANTIDAD DE
DECIMALES)
2, 3 : 5 = 23 : 50 = 0, 46
2, 3 : 5, 6 = 23 : 56 = 0, 4107
2,31: 5, 2 = 231: 520 = 0, 44423
10
10
100
Debemos amplificar dividendo y divisor según el número que tenga mayor cantidad
de decimales, de tal forma que los números que dividamos sean enteros.
En cada caso anterior transformamos la división de decimales en una división de
números enteros amplificando por el factor (potencia de 10) correspondiente destacado.

28. Actividad 4
• Resuelva los siguientes ejercicios y simplifique
si es necesario.
a)
c)
e)
5 6
× =
4 5
3
7,56 × =
2
4,3 : 0, 01 =
b)
d)
f)
7 5
: =
6 9
7,89 :1, 2 =
9
45, 2 × =
3

29. Operaciones combinadas
• Para resolver ejercicios con operatorias
combinadas se debe respetar el siguiente orden:
1º Desarrollar los Paréntesis
2º Desarrollar potencias y Raíces
3º Desarrollar multiplicación y División de
izquierda a derecha
4º Desarrollar Adición y sustracción de
izquierda a derecha

30. Actividad 5
a)
c)
e)
 19 3  7
 − ÷− =
 16 4  8
 10 1  7
1,34 −  × ÷: =
 7 3 4
−5 

3, 24 : 2 ) −  ×0, 21 =
(
9

b)
d)
f)
(
)
6
32, 7 − 3, 01 : =
11
7 5 1
−  − ÷=
6 6 6
 1 1  1 1  1 1 
 + ÷ + ÷ + ÷ =
 2 3  3 4  4 5 

31. Resumen
• Transformación de decimal a fracción y viceversa
• Adición y sustracción de fracciones con igual
denominador, y decimales
• Adición y sustracción de fracciones con distinto
denominador.
• Multiplicación de fracciones y decimales
• División de fracciones y decimales
• Operaciones combinadas con fracciones y
decimales