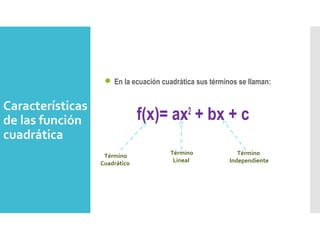
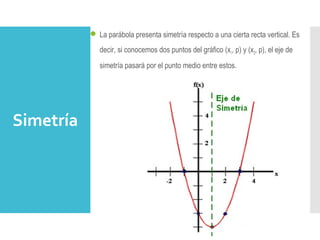
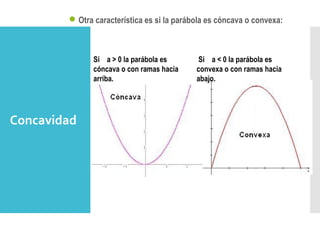
Este documento describe las funciones cuadráticas, incluyendo sus elementos como el término cuadrático, término lineal y término independiente. Explica que las funciones cuadráticas se usan en física y economía para describir movimientos con aceleración constante, trayectorias de proyectiles, ganancias y costos. Además, identifica algunas situaciones que dan lugar a funciones cuadráticas, como determinar el área máxima que se puede cercar con una longitud fija de malla o calcular la temperatura máxima en un

1. Situaciones que dan origen a funciones
cuadráticas
Autora. Olivia Scholz Marbán

2. Objetivo:
Dar a conocer qué es una función cuadrática, sus
elementos y cuáles son las situaciones que dan lugar a una
función cuadrática.
Instrcciones:
Revisa la presentación y una vez comprendido e
identificado su contenido, resuelve las actividades de
rellenar huecos y la de correspondencia.

3. Introducción
 Las funciones cuadráticas son utilizadas en algunas disciplinas
como, por ejemplo, Física y Economía. Son útiles para describir
movimientos con aceleración constante, trayectorias de
proyectiles, ganancias y costos de empresas, y obtener
así información sin necesidad de recurrir a la experimentación.

4. Un poco de
historia
 Siglos antes de resolver algebraicamente la ecuación de
segundo grado, se encontraron soluciones utilizando un
método geométrico, interpretando los términos como áreas, y
distinguiendo varios casos pues no se conocían los números
negativos (y menos aún las áreas negativas). Se sabe que
los matemáticos babilonios alrededor del 400 a.C y los chinos
en el 300 d.C usaban este método para resolver ecuaciones
de segundo grado con raíces positivas. En torno al 300 d.C
Euclides creó un método geómetrico más general (abstracto).

5. Situaciones
que dan
origen a
funciones
cuadráticas
 Un terreno rectangular se desea proteger con una cerca.
¿Cuál es el área máxima que se puede cercar con 110
metros de malla?

6. Temperaturas
 Supongamos que la temperatura de un cierto día de la ciudad
de México luego de t horas pasada la medianoche está dada
por la función:
T(t) =
¿A qué hora la temperatura
fue máxima?
2 01
4 10
4
t t C− + +

7. Proyectiles
 Se arroja un objeto verticalmente hacia arriba con una
velocidad de 80m/seg. Su altura en función del tiempo se
puede aproximar por la fórmula:
2
( ) 4.9 80f t t t= − +

8.  Una función de la forma: f (x) = a x ² + b x + c
con a, b y c pertenecientes a los reales y a ≠ 0, es una
función cuadrática y su gráfico es una curva llamada
parábola.
 Si la ecuación tiene todos los términos se dice ecuación
completa, si a la función le falta el término lineal o
independiente se dice que la ecuación es incompleta.
Características
de las función
cuadrática

9.  En la ecuación cuadrática sus términos se llaman:
f(x)= ax2
+ bx + c
Término
Lineal
Término
Cuadrático
Término
Independiente
Características
de las función
cuadrática

10. Raíces de la función cuadrática Las raíces ( o ceros) de la función cuadrática son aquellos valores
de x para los cuales la expresión vale 0, es decir los valores de x
tales que y = 0. Gráficamente corresponden a las abscisas de los
puntos donde la parábola corta al eje x. Podemos ver a
continuación que existen parábolas que cortan al eje x en:
Raíces

11. Simetría
 La parábola presenta simetría respecto a una cierta recta vertical. Es
decir, si conocemos dos puntos del gráfico (x1, p) y (x2, p), el eje de
simetría pasará por el punto medio entre estos.

12. Vértice
 El vértice de la parábola está ubicado sobre la recta de
simetría, de modo que su coordenada x se calcula:
2
b
x
a
−
=

13. Concavidad
Otra característica es si la parábola es cóncava o convexa:
Si a > 0 la parábola es
cóncava o con ramas hacia
arriba.
Si a < 0 la parábola es
convexa o con ramas hacia
abajo.

14. Ahora ya conoces los elementos que
componen a la función cuadrática y
algunas de sus aplicaciones.

15. Referencias:
 Cruz, V. Familias de funciones: expresiones algebraicas y
sus funciones. Grupo Editorial Iberoamérica. Segunda
edición. México. 2000.
 Miller, et al. Matemática: razonamiento y aplicaciones.
Addison Wesley. Décima edición. México. 2004.
 Oteyza, L. Álgebra, Prentice Hall, México, 2003.