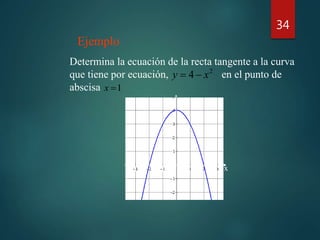
Este documento define conceptos clave relacionados con la derivada de una función y sus aplicaciones. Explica cómo calcular la derivada, los puntos críticos de una función, y cómo determinar los extremos absolutos de una función continua en un intervalo cerrado usando la derivada. También cubre conceptos como la tangente a una curva, la concavidad, y cómo resolver problemas de máximos y mínimos.

1. Tema :
LA DERIVADA DE UNA
FUNCIÓN Y SUS
APLICACIONES
Pablo Segarra P.

2. 2Objetivos:
. Definir la derivada de una función.
. Determinar los puntos críticos de una función.
. Determinar los extremos absolutos de una
función continua en un intervalo cerrado.
. Describir el concepto de punto de inflexión de
una gráfica.
. Analizar la concavidad de una función a
través de su segunda derivada.
. Resolver problemas de máximos y mínimos de
una función en una variable.

3. 3
La Pendiente de una Curva
¿Una curva tiene pendiente?
Entenderemos por pendiente de una
curva a la pendiente de la recta que mas
se asemeja (ajusta) a la curva.
¿y cuál es esta recta?

4. 4
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

5. 5
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

6. 6
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

7. 7
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

8. 8
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

9. 9
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

10. 10
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

11. 11
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

12. 12
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

13. 13
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

14. 14
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

15. 15
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

16. 16
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

17. 17
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

18. 18
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

19. 19
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

20. 20
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

21. 21
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

22. 22
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

23. 23
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
h

24. 24
x
y
0x
)( 0xf )( 0 hxf +
hx +0
h

25. 25
x
y
0x
)( 0xf )( 0 hxf +
hx +0
h

26. 26
x
y
0x
)( 0xf )( 0 hxf +
hx +0
h

27. 27
x
y
0x
)( 0xf )( 0 hxf +
hx +0
h

28. 28
x
y
0x
)( 0xf )( 0 hxf +
hx +0
Tangente!!!

29. 29
x
y
0x
)( 0xf )( 0 hxf +
hx +0

30. 30
x
y
0x
)( 0xf )( 0 hxf +
hx +0

31. 31
x
y
0x
)( 0xf )( 0 hxf +
hx +0

32. La Pendiente de una Curva
32
x
y
0x
)( 0xf
)( 0 hxf +
hx +0
x
y

33. La Pendiente de una Curva
33
h
h
h
)f(x)f(x
limm 00
0
t
+


Es el límite de un cociente de
incrementos
x
)f(xx)f(x
limm 00
0
t



+

x
Si h = x

34. 34
Determina la ecuación de la recta tangente a la curva
que tiene por ecuación, en el punto de
abscisa
2
4 xy 
1x
y
x
Ejemplo

35. Definición de Derivada
35
La derivada de una función f con respecto a la
variable x es la función cuyo valor en x es:
siempre que el límite exista
h
f(x)h)f(x
lim´(x)f
0h
+


Nota 1: f es una función definida en un intervalo
abierto que incluye a x.

36. Observación
36
La derivada de una función es un límite.
Nota 2: Para calcular ese límite se requiere que
la función esté definida en el punto.
a-x
f(a)f(x)
lim
h
f(x)h)f(x
lim
ax0h


+


37. 37
REGLAS DE DERIVACIÓN
4. Si f es derivable y c constante, se tiene:
    xfcxcf 

3. Sea f(x) = xn, entonces:
  1
 n
nxxf
n
1. Sea f(x) = k, entonces:
  0 xf
k
D (c) = 0x
2. Sea f(x) = x, entonces:
  1 xf

38. Reglas de Derivación
38
5. Si f y g son funciones derivables y a y b son
constantes se tiene que:
        xgxfxgxf +

+ 
6. Si f y g son funciones derivables, entonces la
derivada del producto es:
            xgxfxgxfxgxf +

*

39. Reglas de Derivación
39
7. Si f y g son funciones derivables y no es
cero, entonces la derivada del cociente es:
)(xg
)(
)()()()(
)(
)(
2
xg
xgxfxgxf
xg
xf 








8. Si y , entonces la regla de la
cadena se define por:
 n
xgxf )()( 
  )()()(
1
xgxgnxf
n
 
n

40. 40
Observación
Sea y = f(u) donde u = g(x)
Si todas las derivadas involucradas existen, entonces
otra forma de definir la REGLA DE LA CADENA es:
dx
du
du
dy
dx
dy

xuy 

41. 41La función exponecial y=ex y la función
logaritmo natural y= ln x
1 e
e
1
y = ex
y = ln x
x
y

42. 42
Definición:
Si x es cualquier número real, entonces
ln y = x si y sólo si ex = y
Teorema
Si p y q son números reales, entonces
i) ii) iii)qp
q
p
e
e
e 
qpqp
eee +
   pqqp
ee 

43. 43
Derivada de funciones exponenciales
i)
ii)
Derivada de funciones logarítmicas
i)
ii)
x
xfxxf
1
)(;ln)( 
   
 xgexfexf xgxg
 )(;)(
   )(
)(
1
)(;ln)( xg
xg
xfxgxf 
xx
exfexf  )(;)(
Derivadas de funciones EXP y LOG

44. 44
LA DERIVADA
EN EL
ANALISIS DE
FUNCIONES

45. TEOREMA
45
f ’(c) = 0
Si c es un punto de extremo local de f,
entonces

46. PUNTOS CRITICOS
46
Definición:
Un número c del dominio de f se llama
número crítico o punto crítico de f si f ’(c)
0.

47. 47
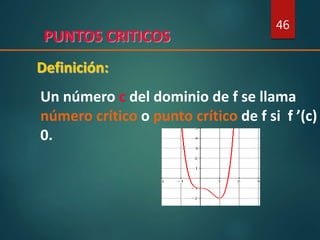
1. Hallar todos los puntos críticos de f en [a, b]
2. Hallar f(c) para cada punto crítico c
3. Calcular f(a) y f(b)
4. El mayor de los números hallados en 2 y 3 es el
máximo absoluto de f en[a,b] y el menor el
mínimo.
Procedimiento para determinar los máximos o
mínimos de una función continua f en [a, b]

48. TEOREMA
48
Sea f continua en [a, b] y derivable en
(a, b), entonces:
Si f ’(x) 0 en (a, b) entonces
f es estrictamente CRECIENTE en [a
>

49. Criterio de la primera derivada
49
Si c es un punto crítico de f y f es
derivable alrededor de c, entonces:
i) Si f ´ cambia de + a - en la vecindad de c
entonces c es un punto de MÁXIMO local de f
ii) Si f ´ cambia de - a + en la vecindad c
entonces c es un punto de MÍNIMO local de f

50. TEOREMA
50
Sea f derivable en el intervalo (a, b), que
contiene a c, tal que existe f ’’(c), entonces:
Si f ’’(c) 0 la gráfica de f es
cóncava hacia
en x = carriba
>
+

51. Agradecimiento
51
PREGUNTAS?
Gracias por su atención

52. Criterio de la segunda derivada
52
Sea c un punto crítico de f en el cual f ’(c) = 0,
entonces,
Si f ’’(c) > 0, c es un punto de
mínimo local
Si f ’’(c) < 0, c es un punto de
máximo local