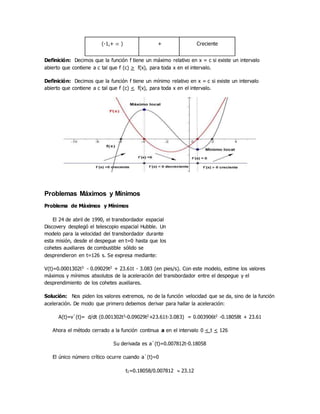
Este documento describe conceptos básicos de cálculo como derivadas, velocidad, aceleración y aplicaciones de la derivada. Explica cómo usar la derivada para encontrar máximos y mínimos de funciones, y cómo calcular la velocidad y aceleración de un objeto que se mueve en línea recta usando derivadas. También cubre temas como funciones implícitas, crecientes/decrecientes, formas indeterminadas y la regla de L'Hôpital.

1. Universidad Tecnológico Antonio José de Sucre
Extensión –Barquisimeto
Aplicaciones de la derivada
Integrante
Miguel A. Pineda
C.I:23.484.983

2. En matemática, laderivadade unafunción esuna medidade larapidezconla que cambiael valor
de dicha funciónmatemática,segúncambieel valorde su variable independiente.Laderivadade
una funciónesunconceptolocal,esdecir,se calculacomo el límite de larapidezde cambiomedia
de la funciónenunciertointervalo,cuandoel intervaloconsideradoparalavariable
independientese tornacada vezmás pequeño.Porellose habladel valorde laderivadade una
ciertafunción enun puntodado
Definicionesde derivada
En terminologíaclásica,ladiferenciación manifiestael coeficiente enque unacantidad cambiaa
consecuenciade uncambioenotra cantidad .
En matemáticas, coeficienteesunfactormultiplicativoque pertenece aciertoobjetocomouna
variable,unvectorunitario,unafunciónbase,etc.
En física, coeficiente esunaexpresiónnuméricaque mediantealgunafórmuladeterminalas
características o propiedadesde uncuerpo.
En nuestrocaso,observandola gráficade laderecha,el coeficiente del que hablamosvendría
representadoenel punto de lafunción porel resultadode ladivisiónrepresentadaporla
relación ,que comopuede comprobarse enlagráfica,esunvalorque se mantiene constante a
lolargo de la línearecta azul que representalatangente enel punto de lafunción.Estoesfácil
de entenderpuestoque el triángulorectángulo formadoenlagráficacon vértice enel punto ,
por muchoque lo dibujemosmásgrande,al serunafiguraproporcional el resultadode es
siempre el mismo.

3. Aplicaciones de la Derivada
La derivadatiene unagranvariedadde aplicacionesademásde darnoslapendiente de latangente
a una curva enun punto.Se puede usarla derivadaparaestudiartasasde variación,valores
máximosymínimosde una función,concavidadyconvexidad
Ejemplo:
Encuentre losmáximosymínimosde laecuación:
Por el criteriode laprimeraderivada.Obtenemoslaprimeraderivadade lafunción:
Encontrandolas raíces para la primeraderivadatenemos:
Por lotanto tenemosalgúnmáximoomínimoenel puntox=0, para determinarsi esunmáximoo
un mínimotendremosque valuarlapendiente antesydespuésde cero,esdecir,ensus
vecindadesde este punto.

4. Evaluandoen y´ (-0.01) tenemos:
y´ (-0.01)= -0.004
Evaluandopara x despuésde cerotenemos:
Y´ (0.01)= 0.004
Como laderivadaalrededorde cerocambiade positivonegativoapositivoportantotenemosun
mínimolocal en(0,0).
Teoremadel ValorMedio:
Si f es continuaenel intervalocerrado[a,b] yderivableenel intervaloabierto(a,b) existeal menos
un númeroc tal que:
“.
Aplicar Derivadas en el Cálculo de Velocidad y Aceleración de un Objeto que
se Mueve en Línea Recta
Una funciónf esderivable enasi f'(a) existe.Esderivable enunintervaloabierto(a,b) (o[a,¥) o (-
¥,a), (-¥,¥)) si esderivable entodonúmerodel intervalo.
Velocidad
Seas =f(t) la funciónposiciónde unobjetoque se muevealolargo de una recta numérica.La
velocidad(instantánea) del objetoenel instantetestádada por:
V(t)=ds /dt= f ´(t)
La velocidadespositivaonegativa,si el objetose desplazaenel sentidopositivoonegativode
la recta numérica.Si lavelocidadesceroel objetoestáenreposo.
Ejemplo:Unobjetose mueve sobre unarectade acuerdoa la ecuacións= 3t2-8t+7
Donde sse mide encentímetrosy t ensegundos
Hallarla velocidaddel objetocuandot=1y cuando t=5
Solución
Tenemosque V(t)=ds/dt = 6t-8 (ds/dt= d(3t2-8t+7) / dt= 6t-8)
Luegov(t)=6(1) - 8= -2 cm/seg(evaluandoparat=1)

5. y v(t)=6(5) - 8= 22 cm/seg(evaluandoparat=5)
Aceleración
Seas= f(t) la funciónposiciónde unobjetoque se muevealolargo de una recta numérica.La
aceleración(instantánea)del objetoenel instante t, estádadapor:
a(t)=dv /dt =f"(t)
Derivación Implícita
No todas las curvas se pueden describir como una sola función. Por ejemplo, la curva
que presenta la ecuación: x2+y2=16 es una circunferencia y no representa una función.
Sin embargo, la semicircunferencia superior sí representa una función; y la semicircunferencia
inferior también la representa. Podemos obtener dos funciones diferentes a partir de esta
circunferencia. Éstas se llaman funciones implícitas.
La circunferencia representada en el dibujo tiene centro en (0,0), y radio 4 su ecuación es
entonces:
x2 + y2 = 16
Esto quiere decir que un punto (x,y) está en la circunferencia, si y sólo si, satisface la ecuación.
Por ejemplo: (0,-4) pertenece a la circunferencia porque:
02 + (-4)2 = 0 + 16 = 16
Efectivamente, estas funciones se pueden obtener despejando y de la ecuación:
x2 + y2 = 16 implica y2 = 16 - x2
Sin embargo, no siempre es factible despejar funciones a partir de una ecuación dada, aunque
sepamos que hay dos o más funciones implícitas definidas. Y, aún así, podríamos estar interesados
en, por ejemplo, determinar la ecuación de la recta tangente a la curva en algunos de sus puntos.
Resulta que es posible derivar una función implícita aun cuando no podamos despejarla de la
ecuación que la define. Basta sencillamente con derivar ambos miembros de la ecuación que la
define, teniendo en cuenta, eso sí, que una de las variables es función de la otra. El siguiente
ejemplo ilustra el método llamado derivación implícita.
Ejemplo 1
Cálculo de la Derivada en un Punto de la Circunferencia
Considere que y es una función de x definida por la siguiente ecuación: x2 + y2 = 16

6. Determinar y' y encontrar su valor en el punto (3,7). Solución Vamos a derivar a ambos lados
de la ecuación, pero teniendo el cuidado de recordar que y es función de x: x2 + y2=16
(x2+y2)' = (16)' (vamos a derivar ambos miembros)
2x+2y·y'= 0 aplicamos la regla ([f(x)]n)'=n[f(x)]n-1·f'(x))
2y·y'=-2x y'=-2x/2y y'=-x/y
Ahora, en el punto (3,7) tenemos x=3, y=7. Por lo tanto, aquí se tiene y'=-3/7.
funciones Crecientes y Decrecientes:
Definición
1. Se dice que una función f definida en un
intervalo es creciente, si sólo si, f(x1) < f(x2),
siempre que x1< x2 donde x1 y x2 son dos
números cualesquiera en el intervalo.
2. Se dice que una función f definida en un
intervalo es decreciente en ese intervalo, si y
sólo si, f(x1) > f(x2), siempre que x1< x2,
donde x1 y x2 son dos números cualesquiera en el intervalo.
Ejemplo: Dadas las siguientes funciones, determinar los intervalos de crecimiento y decrecimiento:
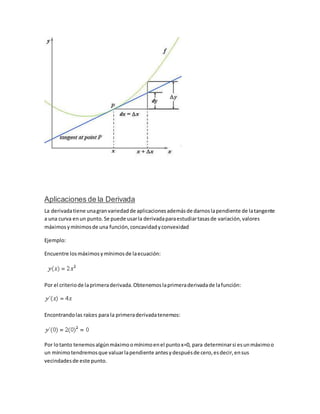
1. f(x)=3x+8
Solución f´(x)=3
Se observa que f´(x)=3>0 para todo x en R. En consecuencia, la función es creciente en R.
2. f(x)=x2+2x-3
Solución: f´(x)=2x+2. Necesitamos saber si existe para x algún valor tal que f´(x)=0, donde la
función f no es creciente ni decreciente.
2x+2=0
x = -1. Es decir para x = -1 esta función no es creciente ni decreciente. Estudiaremos el
comportamiento de la derivada antes y después de x=-1 f´(x)=2(x+1).
Intervalo F´(X) La Función es
(- ,1) - Decreciente

7. (-1,+  ) + Creciente
Definición: Decimos que la función f tiene un máximo relativo en x = c si existe un intervalo
abierto que contiene a c tal que f (c) > f(x), para toda x en el intervalo.
Definición: Decimos que la función f tiene un mínimo relativo en x = c si existe un intervalo
abierto que contiene a c tal que f (c) < f(x), para toda x en el intervalo.
Problemas Máximos y Mínimos
Problema de Máximos y Mínimos
El 24 de abril de 1990, el transbordador espacial
Discovery desplegó el telescopio espacial Hubble. Un
modelo para la velocidad del transbordador durante
esta misión, desde el despegue en t=0 hasta que los
cohetes auxiliares de combustible sólido se
desprendieron en t=126 s. Se expresa mediante:
V(t)=0.0001302t3 - 0.09029t2 + 23.61t - 3.083 (en pies/s). Con este modelo, estime los valores
máximos y mínimos absolutos de la aceleración del transbordador entre el despegue y el
desprendimiento de los cohetes auxiliares.
Solución: Nos piden los valores extremos, no de la función velocidad que se da, sino de la función
aceleración. De modo que primero debemos derivar para hallar la aceleración:
A(t)=v`(t)= d/dt (0.001302t3-0.09029t2+23.61t-3.083) = 0.003906t2 -0.18058t + 23.61
Ahora el método cerrado a la función continua a en el intervalo 0 < t < 126
Su derivada es a`(t)=0.007812t-0.18058
El único número crítico ocurre cuando a`(t)=0
t1=0.18058/0.007812  23.12

8. Al evaluar a(t) en el número crítico y los extremos tenemos:
a(0)=23.61 a(t1) 21.52 a(126)  62.87
Formas Indeterminadas
Si una función toma para ciertos valores de la
variable una de las formas siguientes:
entonces decimos que es indeterminada.
Si se tiene,
En este caso fue fácil evitar la discontinuidad presentada, pero no siempre es así. Por eso,
cuando tenemos expresiones más complejas, existe una regla que se conoce como regla de
L´Hopital. Teorema:
Dadas f y g funciones diferenciables en un intervalo abierto I, excepto posiblemente en el
número a en I, y supongamos que para toda x  a en I, g`(x)  0. Entonces, si límite cuando x
tiende a de f(x) es más o menos infinito y límite cuando x tiende a "a" de g(x) = más o menos infinito
y si límite cuando x tiende a "a" del cociente de las respectivas derivadas de las funciones existe,
entonces el límite cuando x tiende a "a", también existe y tendrá el mismo valor.
Nota: Esta regla es aplicable a formas 0/0 ó  / .
Aplicación de la regla para determinar el valor de la forma 0 / 0 ó  / :
Se halla la derivada del numerador para obtener un nuevo numerador, se halla la derivada del
denominador para obtener un nuevo denominador. El valor de esa nueva fracción, para el valor
asignado de la variable, será el valor límite de la primera fracción.