1) El documento describe los saberes matemáticos que los estudiantes deben aprender en 4to grado, incluyendo números enteros, fracciones y decimales, así como sumas, restas, multiplicaciones y divisiones.
2) Se enfatiza que la complejidad de las tareas depende del tipo de relación entre los datos y no necesariamente de la cantidad de cifras de los números.
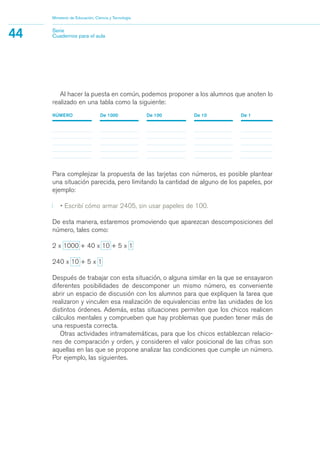
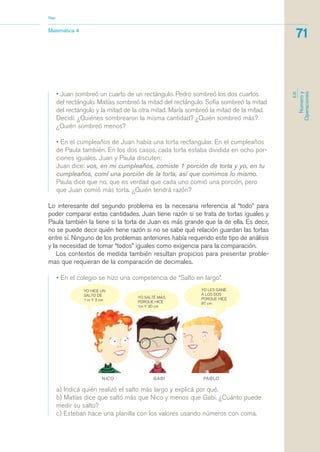
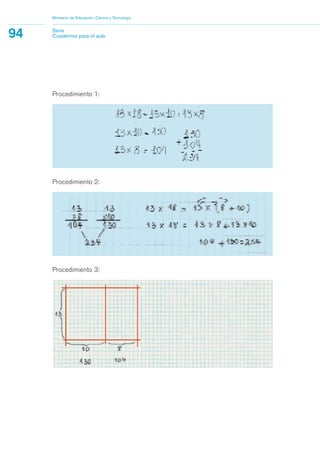
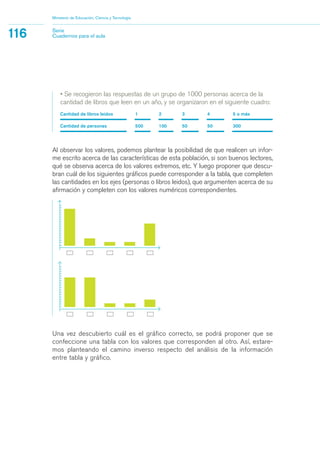
3) Se proveen ejemplos de actividades para que los estudiantes desarrollen dichos saberes a través de la resolución de problemas de contextos reales y matemá