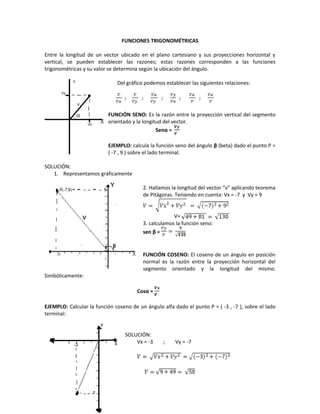
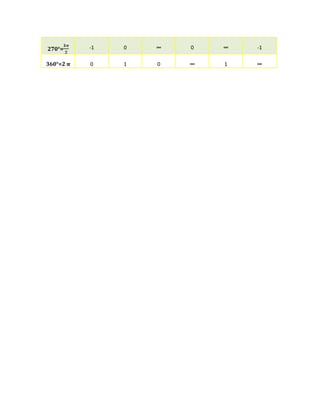
Las funciones trigonométricas relacionan la longitud de un vector y sus proyecciones horizontal y vertical mediante razones matemáticas. Se definen las funciones seno, coseno y tangente y se explican sus valores para ángulos específicos como 30°, 45° y 60°. También se describen las funciones inversas cotangente, cosecante y secante y las relaciones entre las funciones trigonométricas para ángulos negativos y cuadrantes.

1. FUNCIONES TRIGONOMÉTRICAS
Entre la longitud de un vector ubicado en el plano cartesiano y sus proyecciones horizontal y
vertical, se pueden establecer las razones; estas razones corresponden a las funciones
trigonométricas y su valor se determina según la ubicación del ángulo.
Del gráfico podemos establecer las siguientes relaciones:
FUNCIÓN SENO: Es la razón entre la proyección vertical del segmento
orientado y la longitud del vector.
Senα =
EJEMPLO: calcula la función seno del ángulo β (beta) dado el punto P =
( -7 , 9 ) sobre el lado terminal.
SOLUCIÓN:
1. Representamos gráficamente
2. Hallamos la longitud del vector “v” aplicando teorema
de Pitágoras. Teniendo en cuenta: Vx = -7 y Vy = 9
V=
3. calculamos la función seno:
sen β =
FUNCIÓN COSENO: El coseno de un ángulo en posición
normal es la razón entre la proyección horizontal del
segmento orientado y la longitud del mismo.
Simbólicamente:
Cosα =
EJEMPLO: Calcular la función coseno de un ángulo alfa dado el punto P = ( -3 , -7 ), sobre el lado
terminal:
SOLUCIÓN:
Vx = -3 ; Vy = -7

2. Cosα = =
FUNCIÓN TANGENTE: La tangente de un ángulo en posición normal es la razón entre la proyección
vertical y la proyección horizontal del vector; se debe tener en cuenta que la proyección horizontal
no puede ser cero. Simbólicamente se representa así:
Tanα =
EJEMPLO: calcular el valor de la tangente del ángulo formado P = (4 , -3), sobre el lado terminal.
SOLUCIÓN: Tanα = =
FUNCIÓN COTANGENTE: La función cotangente es la recíproca de la tangente y se define como el
cociente entre la proyección horizontal y la proyección vertical. Simbólicamente se representa así:
Cot α =
FUNCIÓN SECANTE: Es la función recíproca del coseno, y se define como el cociente entre la
longitud del vector y su proyección horizontal, así:
Secα =
FUNCIÓN COSECANTE: Es la función recíproca del seno; se define como la razón entre la longitud
del vector y su proyección vertical; así:
Cscα =

3. EJEMPLO: Hallar el valor de las funciones trigonométricas de un ángulo determinado cuyo lado
terminal es el punto P = (-5 , 3).
SOLUCIÓN: Identificamos los elementos: Vx = -5 ; Vy = 3 y V, lo calculamos mediante el
teorema de Pitágoras.
senα = Tanα = = Secα =
Cosα = = Cot α = Cscα =
FUNCIONES TRIGONOMÉTRICAS INVERSAS MULTTIPLICATIVAS
De acuerdo con las anteriores definiciones se satisfacen las siguientes relaciones:
Cot θ = ; Sec θ = ; Csc θ =
EJEMPLO:
a. Determinar las funciones coseno y tangente del ángulo x, si: Secx = -1.2 y Cotx = -2
b. Si el ; Sec θ= y tan θ = ; Hallar las demás funciones trigonométricas
Solución: a. como, Sec x = =
Tanx =
b. = =
Cot θ =
Csc θ =
SIGNO DE LAS FUNCIONES TRIGONOMÉTRICAS SEGÚN EL CUADRANTE
Función Sen Cos Tan Cot Sec Csc
Cuadrante
I + + + + + +

4. II + - - - - +
III - - + + - -
IV - + - - + -
ACTIVIDAD
1. Encuentra el valor de las funciones trigonométricas de los ángulos determinados por
el vector cuyo extremo es:
a. P = (4,3) b. A = (-3,-5) c. Q = (-4, 4) d. R= (5, -3)
2. Las coordenadas del extremo de un vector situado en posición normal son P = .
Calcula el valor de las siguientes expresiones:
a. Sen θ + cos θ b. tan θ c. 5sen θ + 2 cos θ
d. tan θ + cot θ e. tan² θ - sen²θ f.
FUNCIONES DE ÁGULOS ESPECIALES
FUNCIONES PARA ÁNGULOS DE 30° Y 60°
h=
h= L
Funciones para ángulos de 30°
Sen 30° = tan 30° =
Cos 30° = = cot 30° =
Sec 30° = csc 30° =
Funciones para ángulos de 60°

5. Sen 60° = cot 60°=
Cos 60° = sec 60° =
Tan 60° = csc 60° =
Funciones para el ángulo de 45°
h=
sen 45° = tan 45° = sec 45° =
cos 45° = cot 45° = csc 45° =
RESUMEN DE LAS FUNCIONES PARA ÁNGULOS ESPECIALES
Función sen cos tan cot sec csc
Ángulo
30° =
60° =
1 1
45°=
FUNCIONES TRIGONOMÉTRICAS DE ÁNGULOS NEGATIVOS

6. Para los ángulos anteriores podemos establecer las funciones trigonométricas:
Para los ángulos de primer gráfico para los ángulos del segundo gráfico:
sen α = sen (-α) = sen α = sen (-α) =
cos α= cos (-α)= cos α= cos (-α)=
tan α= tan (-α)= tan α= tan (-α)=
Se deduce entonces que para cualquier ángulo alfa (α) se cumplen las siguientes relaciones:
sen (-α) = -sen α cot (-α) = -cot α
cos (-α)= cos α sec (-α) = sec α
tan (-α) = - tan α csc (-α) = - csc α
FUNCIONES DE ÁNGULOS CUADRANTES
FUNCIONES Sen Cos tan cot sec csc
ÁNGULO
0° 0 1 0 ∞ 1 ∞
90° 1 0 ∞ 0 ∞ 1
180°= 0 -1 0 ∞ -1 ∞

7. 270°= -1 0 ∞ 0 ∞ -1
360°=2 0 1 0 ∞ 1 ∞