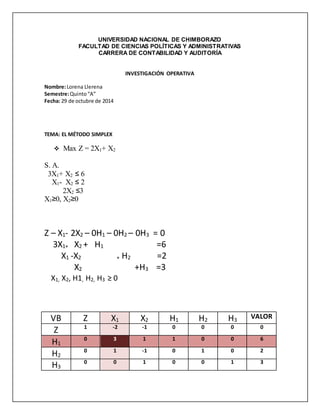
El documento presenta un problema de programación lineal para maximizar las utilidades de una fábrica de muebles. La función objetivo depende de la producción de mesas, sillas, camas y bibliotecas. Está sujeto a restricciones en el uso de los recursos. El método simplex se utiliza para encontrar la solución óptima de X1 = 0, X2 = 7, X3 = 6, X4 = 4, con una utilidad máxima de $340000.

1. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLÍTICAS Y ADMINISTRATIVAS
CARRERA DE CONTABILIDAD Y AUDITORÍA
INVESTIGACIÓN OPERATIVA
Nombre: Lorena Llerena
Semestre: Quinto “A”
Fecha: 29 de octubre de 2014
TEMA: EL MÉTODO SIMPLEX
 Max Z = 2X1+ X2
S. A.
3X1+ X2 ≤ 6
X1- X2 ≤ 2
2X2 ≤3
X1≥0, X2≥0
Z – X1- 2X2 – 0H1 – 0H2 – 0H3 = 0
3X1+ X2 + H1 =6
X1 -X2 + H2 =2
X2 +H3 =3
X1, X2, H1, H2, H3 ≥ 0
VB Z X1 X2 H1 H2 H3 VALOR
Z 1 -2 -1 0 0 0 0
H1
0 3 1 1 0 0 6
H2
0 1 -1 0 1 0 2
H3
0 0 1 0 0 1 3

2. VB Z X1 X2 H1 H2 H3 VALOR
Z 1 0 -1/3 2/3 0 0 4
X1
0 1 1/3 1/3 0 0 2
H2
0 -1 -4/3 -1/3 1 0 0
H3
0 0 1 0 0 1 3
VB Z X1 X2 H1 H2 H3 VALOR
Z 1 0 0 2/3 0 1/3 5
X1
0 1 0 1/3 0 1/3 1
H2
0 -1 0 -1/3 1 4/3 0
X2
0 0 1 0 0 1 3
Z=5
X1=1
H2 =0
X2 =3
Z = 2x1+ x2
2(1) +3
= 5//
 La empresa el SAMÁN Ltda. Dedicada a la fabricación de muebles, ha ampliado su
producción en dos líneas más. Por lo tanto actualmente fabrica mesas, sillas, camas
y bibliotecas. Cada mesa requiere de 2 piezas rectangulares de 8 pines, y 2 piezas
cuadradas de 4 pines. Cada silla requiere de 1 pieza rectangular de 8 pines y 2
piezas cuadradas de 4 pines, cada cama requiere de 1 pieza rectangular de 8 pines, 1

3. cuadrada de 4 pines y 2 bases trapezoidales de 2 pines y finalmente cada biblioteca
requiere de 2 piezas rectangulares de 8 pines, 2 bases trapezoidales de 2 pines y 4
piezas rectangulares de 2 pines. Cada mesa cuesta producirla $10000 y se vende en
$ 30000, cada silla cuesta producirla $ 8000 y se vende en $ 28000, cada cama
cuesta producirla $ 20000 y se vende en $ 40000, cada biblioteca cuesta producirla
$ 40000 y se vende en $ 60000. El objetivo de la fábrica es maximizar las
utilidades.
La función Objetivo:
MAX
Z= 20000 X1 + 20000 X2+ 20000 X3 + 20000 X4
S.A
2X1 + X2 + X3 + 2X4 ≤ 24
2X1 + 2X2 + X3≤ 20
2X3 + 2X4 ≤ 20
4X4≤ 16
X1 ≥0, X2≥0, X3 ≥0, X4 ≥0

4. Z- 20000 X1 - 20000 X2- 20000 X3 - 20000 X4 – 0H1 – 0H2 – 0H3 - 0H4 = 0
2X1 + X2 + X3 + 2X4 + H1 =24
2X1 + 2 X2 + X3 + + H2 =20
2X3 + 2X4 + H3 =20
4X4 + H4 =16
X1, X2, X3, X4, H1, H2, H3, H4 ≥ 0
VB Z X1 X2 X3 X4 H1 H2 H3 H4 VALOR
Z 1 -20000 -20000 -20000 -20000 0 0 0 0 0
H1 0 2 1 1 2 1 0 0 0 24
H2 0 2 2 1 0 0 1 0 0 20
H3 0 0 0 2 2 0 0 1 0 20
H4 0 0 0 0 4 0 0 0 1 16
VB Z X1 X2 X3 X4 H1 H2 H3 H4 VALOR
Z 1 0 0 -10000 -20000 0 10000 0 0 200000
H1 0 1 0 0,5 2 1 -0,5 0 0 14
X 2 0 1 1 0,5 0 0 0,5 0 0 10
H3 0 0
0
2 2 0 0 1 0 20
H4 0 0
0
0 4 0 0 0 1 16

5. VB Z X1 X2 X3 X4 H1 H2 H3 H4 VALOR
Z 1 0 0 -10000 0 0 10000 0 5000 280000
H1 0 1 0 0,5 0 1 -0,5 0 -0,5 6
X 2 0 1 1 0,5 0 0 0,5 0 0 10
H3 0 0
0
2 0 0 0 1 -0,5 12
x4 0 0
0
0 1 0 0 0 0,25 4
VB Z X1 X2 X3 X4 H1 H2 H3 H4 VALOR
Z 1 0 0 0 0 0 10000 5000 2500 340000
H1 0 1 0 0 0 1 -0,5 -0,25 -0,38 3
X 2 0 1 1 0 0 0 0,5 -0,25 0,13 7
x3 0 0 0 1 0 0 0 0,5 -0,25 6
x4 0 0 0 0 1 0 0 0 0,25 4
Z = 340000
H1=3
x1=0
X2=7
x3=6
x4=4

6. Z= 20000 X1 + 20000 X2+ 20000 X3 + 20000 X4
= 20000(0)+ 20000(7)+ 20000(6)+ 20000(4)
= 340000//
 MAXIMIZAR:
Sujeto a:
Z – X1- 2X2 – 0H1 – 0H2 = 0
O.75X1 + X2 + H1 =6
0.5X1 + X2 + H2 =5
X1, X2, H1, H2, ≥ 0
VB Z X1 X2 H1 H2 VALOR
Z 1 -1 -2 0 0 0
H1
0 0.75 1 1 0 6
H2
0 0.5 1 0 1 5
VB Z X1 X2 H1 H2 VALOR
Z 1 3 0 0 2 10
H1
0 -1.25 0 1 -1 1
X2
0 2 1 0 1 5

7. Z= 10
H1 =1
X1 =0
X1 =5
Z = X1+ 2X1
= (0) + 2(5)
= 10
 Max Z = X1+ X2
S. A.
X1+3 X2 ≤ 26
4 X1+3X2 ≤ 44
2X1 +3X2 ≤28
x1≥0, x2≥0
Z – X 1 - X2 – 0H1 – 0H2 – 0H3 = 0
X1 + 3 X2 + H1 =26
4X1+ 3 X2 + H2 =44
2X1+ 3 X2 +H3 =28
X1, X2, H1, H2, H3 ≥ 0
VB Z X1 X2 H1 H2 H3 VALOR
Z 1 -1 -1 0 0 0 0
H1
0 1 3 1 0 0 26
H2
0 4 3 0 1 0 44
H3
0 2 3 0 0 1 28

8. VB Z X1 X2 H1 H2 H3 VALOR
Z 1 -2/3 0 1/3 0 0 26/3
X2
0 1/3 1 1/3 0 0 26/3
H2
0 3 0 -1 1 0 18
H3
0 1 0 -1 0 1 2
VB Z X1 X2 H1 H2 H3 VALOR
Z 1 0 0 -1/3 0 2/3 10
X2
0 0 1 2/3 0 1/3 8
H2
0 0 0 2 1 -3 12
X1
0 1 0 -1 0 1 2
VB Z X1 X2 H1 H2 H3 VALOR
Z 1 0 0 0 1/6 1/6 12
X2
0 0 1 0 -1/3 2/3 4
H2
0 0 0 1 1/2 -3/2 6
X1
0 1 0 0 1/2 -1/2 8
Z = 12
X2 =4
H2 =6
X1 =8
Z = X1+ X2
= 8+4
= 12